电场对电荷有作用力,为了从力的角度描述电场,引入了电 场强度 E 这个物理量,场强函数 E(x,y,z) 描述了整个静电场的 空间分布。电场力对带电体做功,使带电体在电场中具有了能 量,因此从功和能的角度同样可以描述电场。首先需要引入一个 新的物理量——电势能。
5.3.1 电势能
前面已表明,静电力(场)是保守力(场),而在力学中已阐明,保守力的功等于势能增量的负值,即
W f i t = − Δ E p = − ( E p h − E p g ) W_{\rm fit} = -\Delta E_{\rm p} = -(E_{\rm ph} - E_{\rm pg}) W fit = − Δ E p = − ( E ph − E pg ) 式中, E a b E_{ab} E ab E a a E_{aa} E aa
同样,在电场 E 中将检验电荷 q 0 q_0 q 0 F = q 0 E F = q_0 E F = q 0 E
W a b = ∫ a b F ⋅ d l = q 0 ∫ a b E ⋅ d l = − ( E p b − E p a ) ( 5.3.1 ) W_{ab} = \int_{a}^{b} \mathbf{F} \cdot d\mathbf{l} = q_0 \int_{a}^{b} \mathbf{E} \cdot d\mathbf{l} = -(E_{pb} - E_{pa}) \qquad (5.3.1) W ab = ∫ a b F ⋅ d l = q 0 ∫ a b E ⋅ d l = − ( E p b − E p a ) ( 5.3.1 ) 式中 E p b E_{pb} E p b E p a E_{pa} E p a q 0 q_0 q 0
W a b = − ( E p b − E p a ) = − q q 0 4 π ε 0 ( 1 r b − 1 r a ) W_{ab} = -(E_{pb} - E_{pa}) = -\frac{qq_0}{4\pi\varepsilon_0} \left(\frac{1}{r_b} - \frac{1}{r_a}\right) W ab = − ( E p b − E p a ) = − 4 π ε 0 q q 0 ( r b 1 − r a 1 ) (5.3.2)
式中, r a r_a r a r b r_b r b q a q_a q a
电势能同其他势能一样,是一个相对量,只有选定参考的电势能零点之后,才有可能确定电场中任意点处的电势能。
在式(5.3.1)中,设想作用于 q 0 q_0 q 0 q 0 q_0 q 0 r b → ∞ r_b \to \infty r b → ∞ q 0 q_0 q 0 q 0 q_0 q 0 r b → ∞ r_b \to \infty r b → ∞ q 0 q_0 q 0 V x V_x V x q 0 q_0 q 0
W a ∞ = q 0 ∫ a ∞ E ⋅ d l = E p a W_{a\infty} = q_0 \int_a^{\infty} \mathbf{E} \cdot d\mathbf{l} = E_{pa} W a ∞ = q 0 ∫ a ∞ E ⋅ d l = E p a (5.3.3)
上式说明检验电荷 q 0 q_0 q 0 E p a E_{pa} E p a q 0 q_0 q 0
在点电荷 q 产生的电场中, q 0 q_0 q 0
W a ∞ = E p a = q 0 ∫ a ∞ E ⋅ d l = q q 0 4 π ε 0 r a W_{a\infty} = E_{pa} = q_0 \int_a^{\infty} E \cdot dl = \frac{qq_0}{4\pi\varepsilon_0 r_a} W a ∞ = E p a = q 0 ∫ a ∞ E ⋅ d l = 4 π ε 0 r a q q 0 (5.3.4)
如果电场是由若干个点电荷构成的电荷系产生,则 q 0 q_0 q 0
产生电势能的代数和,这一原理称为电势能的叠加原理,即
E p a = q 0 4 π ε 0 ∑ i q i r i E_{pa} = \frac{q_0}{4\pi\varepsilon_0} \sum_{i} \frac{q_i}{r_i} E p a = 4 π ε 0 q 0 i ∑ r i q i (5.3.5)
式中, r i r_i r i q i q_i q i
如果电场是由电荷连续分布的带电体产生,则 a 处电势能为
E p a = q 0 4 π ϵ 0 ∫ V ρ d V r E_{pa} = \frac{q_0}{4\pi\epsilon_0} \int_{V} \frac{\rho \, dV}{r} E p a = 4 π ϵ 0 q 0 ∫ V r ρ d V (5.3.6)
式中,r 是电荷元 d q = ρ d V dq = \rho dV d q = ρ d V q 0 q_0 q 0
应当指出,电荷 q 0 q_0 q 0 q 0 q_0 q 0 q 0 q_0 q 0
5.3.2 电势
静电场是有源场还是无源场?是 保守场还是非保守场?或者是有 旋场还是无旋场?
由上可知,电势能不仅与位置有关,还与检验电荷 q 0 q_0 q 0 E p a q 0 \frac{E_{pa}}{q_0} q 0 E p a
V a = E p a q 0 = W a ∞ q 0 = ∫ a ∞ E ⋅ d l V_a = \frac{E_{pa}}{q_0} = \frac{W_{a\infty}}{q_0} = \int_a^{\infty} \mathbf{E} \cdot d\mathbf{l} V a = q 0 E p a = q 0 W a ∞ = ∫ a ∞ E ⋅ d l (5.3.7)
V a V_a V a
在国际单位制中,电势的单位是 J ⋅ C − 1 J \cdot C^{-1} J ⋅ C − 1
依式(5.3.7)可得静电场中任意的两个位置 a ∖ b a \setminus b a ∖ b U a b U_{ab} U ab
U a b = V a − V b = ∫ a b E ⋅ d l U_{ab} = V_a - V_b = \int_a^b \mathbf{E} \cdot d\mathbf{l} U ab = V a − V b = ∫ a b E ⋅ d l (5.3.8)
电势差的单位与电势的单位相同,也为 V( 伏特) 。其物理意义为,将单位正电荷由 a 点移到 b 点静电场力所做的功。由此可
以求出将 q 0 q_0 q 0 W a b = q 0 ( V a b = q 0 ( V a b − V b b ) W_{ab} = q_0(V_{ab} = q_0(V_{ab} - V_{bb}) W ab = q 0 ( V ab = q 0 ( V ab − V bb )
正如以上所述,电势与电势能一样,都是相对量,其数值的大小与零电势(能)点的取值有关。当改变零电势(能)的位置时,某点的电势(能)也随之而变,但是在电场中,两点间电势差的数值却与零电势(能)位置的选取无关。因此,与电势相比电势差更为实用。在电子技术和电工学中常将地球选为零电势点。
5.3.3 电势的计算
计算电势所依据的基本公式是式(5.3.7)。设想在点电荷 q 产生的电场中,距离该点电荷为r 处的电势函数为
V ( r ) = E p ( r ) q 0 = q 4 π ε 0 r V(r) = \frac{E_{p}(r)}{q_{0}} = \frac{q}{4\pi\varepsilon_{0}r} V ( r ) = q 0 E p ( r ) = 4 π ε 0 r q (5. 3. 10)
如果产生电场的是一个分立的点电荷系,每个点电荷 q i q_i q i V i V_i V i
V i = q i 4 π ε 0 r i V_i = \frac{q_i}{4\pi\varepsilon_0 r_i} V i = 4 π ε 0 r i q i 式中 , r i ,r_i , r i q i q_i q i
V = ∑ V i = ∑ i q i 4 π ε 0 r i V = \sum V_i = \sum_i \frac{q_i}{4\pi\varepsilon_0 r_i} V = ∑ V i = i ∑ 4 π ε 0 r i q i (5. 3. 11)
对分布于有限区域的连续带电体在空间某点处产生的电势, 上式中的 V i V_i V i d V = d q 4 π ε 0 r dV = \frac{dq}{4\pi\varepsilon_0 r} d V = 4 π ε 0 r d q
V = 1 4 π ε 0 ∫ d q r (5.3.12) V = \frac{1}{4\pi\varepsilon_0} \int \frac{\mathrm{d}q}{r} \tag{5.3.12} V = 4 π ε 0 1 ∫ r d q ( 5.3.12 ) 积分遍布整个带电体。积分时将式中电荷元 dq 与电荷所在处的几何元联系起来可简化积分。
若电荷连续地分布在一条曲线、一个曲面或一个体积中,则电荷元分别表示为 d q = λ d l dq = \lambda dl d q = λ d l d q = σ d S dq = \sigma dS d q = σ d S d q = ρ d V dq = \rho dV d q = ρ d V λ \lambda λ σ \sigma σ ρ \rho ρ
在静电场 E 函数已知的情况下,则可依式(5.3.7)计算出电场中任意点 a 处的电势为
V a = ∫ a c E ⋅ d l V_a = \int_a^c \boldsymbol{E} \cdot d\boldsymbol{l} V a = ∫ a c E ⋅ d l (5.3.13)c c c c c c b b b
式中,c 表示电势零点处的位置。当点 c 由电场中任意点 b 替代时,式(5.3.13)则表示 a、b 两点的电势差。
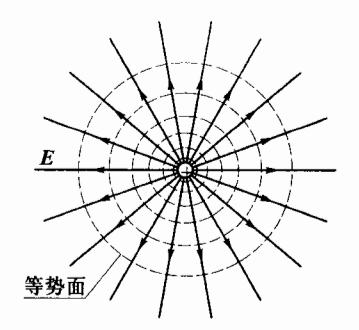
图 5-21 点电荷等势面
图 5-22 电场线与等势面关系的 证明
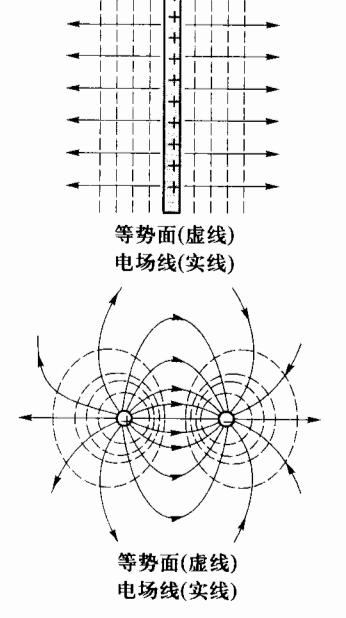
图 5-23 电场线与等势面的关系
前面曾经用电场线形象地描述场强分布,本节为了形象地描述电势在空间的分布而引入等势面。所谓等势面就是电场中所有电势相等的点构成的曲面。
对于真空中孤立的点电荷 q 而言,由它在空间的电势分布函数 V ( r ) = q 4 π ε 0 r V(r) = \frac{q}{4\pi\varepsilon_0 r} V ( r ) = 4 π ε 0 r q
一般说来,静电场中电势是逐点变化的,若将每个不同的等势面都描绘出来,既不可能,也没必要。所以等势面间有一定的距离,这个距离表征等势面间的电势差,并且规定相邻等势面的电势差为一常量。根据等势面在电场中的分布可以判断,等势面密集的区域场强数值较大;稀疏的区域场强的数值较少。
对于点电荷 q 而言,电场线是以 q 为起点的辐射线。因此,电场线与等势面处处是彼此垂直的,并且电场线的方向指向电势降落的方向,如图 5-21 所示。这一结论适用于任何形状的带电体所产生的场强。
为证明电场线与等势面垂直,可以设想,在静电场中某处的电场线与其相交的等势面不相垂直,E 与等势面的夹角为 α \alpha α E / / = E cos α E_{//}=E\cos\alpha E // = E cos α E / / E_{//} E // d I = E cos α d I dI=E\cos\alpha dI d I = E cos α d I d V = E cos α d I = 0 dV=E\cos\alpha dI=0 d V = E cos α d I = 0 cos α = 0 \cos\alpha=0 cos α = 0 α = π 2 \alpha=\frac{\pi}{2} α = 2 π
5.3.5 场强与电势的关系
场强与电势都是用来描述静电场性质的物理量,故两者之间
必然存在着某种联系。在已知场强函数时,依据式(5.3.13)通过积分运算,可求得电势函数或电位差。同样,在已知电势函数时,通过微分运算也可以得出场强函数。
如图 5-24 所示,两个距离为无穷小的等势面 M 和 N,设 M 面电势高于 N 面电势,电势差为 dV。过 a 点取 N 面的单位法线 矢量 e n e_n e n e n e_n e n
d V = E ⋅ d l = − E cos α d l = − E l d l dV = E \cdot dl = -E \cos \alpha dl = -E_l dl d V = E ⋅ d l = − E cos α d l = − E l d l 式中, E t = E cos α E_t = E \cos \alpha E t = E cos α d V = E t d l dV = E_t dl d V = E t d l
− ∂ V ∂ l = E i (5.3.14) -\frac{\partial V}{\partial l} = E_i \tag{5.3.14} − ∂ l ∂ V = E i ( 5.3.14 ) 其物理意义为:电势 V 沿 l 方向变化率的负值,等于电场 E 在该方向上的分量。 ∂ V ∂ l \frac{\partial V}{\partial l} ∂ l ∂ V E = E x i + E y j + E z k E=E_x i+E_y j+E_z k E = E x i + E y j + E z k
E x = − ∂ V ∂ x , E y = − ∂ V ∂ y , E z = − ∂ V ∂ z E_x = -\frac{\partial V}{\partial x}, \quad E_y = -\frac{\partial V}{\partial y}, \quad E_z = -\frac{\partial V}{\partial z} E x = − ∂ x ∂ V , E y = − ∂ y ∂ V , E z = − ∂ z ∂ V 因此
E = − ∂ V ∂ x i − ∂ V ∂ y j − ∂ V ∂ z k = − ( ∂ V ∂ x i + ∂ V ∂ y j + ∂ V ∂ z k ) = − ∇ V = − grad V \boldsymbol{E} = -\frac{\partial V}{\partial x} \boldsymbol{i} - \frac{\partial V}{\partial y} \boldsymbol{j} - \frac{\partial V}{\partial z} \boldsymbol{k} = -\left(\frac{\partial V}{\partial x} \boldsymbol{i} + \frac{\partial V}{\partial y} \boldsymbol{j} + \frac{\partial V}{\partial z} \boldsymbol{k}\right) = -\nabla V = -\text{grad } V E = − ∂ x ∂ V i − ∂ y ∂ V j − ∂ z ∂ V k = − ( ∂ x ∂ V i + ∂ y ∂ V j + ∂ z ∂ V k ) = − ∇ V = − grad V 即
上式中的" ∇ \nabla ∇ ∇ \nabla ∇
∇ = ∂ ∂ x i + ∂ ∂ y j + ∂ ∂ z k \nabla = \frac{\partial}{\partial x} \mathbf{i} + \frac{\partial}{\partial y} \mathbf{j} + \frac{\partial}{\partial z} \mathbf{k} ∇ = ∂ x ∂ i + ∂ y ∂ j + ∂ z ∂ k 电势梯度 ▼ V 的物理意义为:电势沿着它增加最快方向上的增加率,即沿着等势面法线方向的增加率。
仍以图 5-24 为例,在等势面 M 和 N 之间,最短的路径为沿着单位法线矢量 e n e_n e n d n / cos α dn/\cos\alpha d n / cos α
∂ V ∂ n > ∂ V ∂ l \frac{\partial V}{\partial n} > \frac{\partial V}{\partial l} ∂ n ∂ V > ∂ l ∂ V
图 5-24 场强与电势的关系
于是 ∇ V = ∂ V ∂ n e n \nabla V = \frac{\partial V}{\partial n} e_n ∇ V = ∂ n ∂ V e n V ⋅ m − 1 V \cdot m^{-1} V ⋅ m − 1 N ⋅ C − 1 N \cdot C^{-1} N ⋅ C − 1
到此,本节又提供了一种求场强函数的方法,即在已知电荷分布情况下,先求电势函数 V,再通过求它的梯度来确定场强函数 E。
例题 5~8
求电偶极子电场中的电势分布。
解:电偶极子可视为点电荷系,如图 5-25 所示。在电偶极子形成的电场中,任选点 P,由点电荷电势表达式和叠加原理得
V = V 1 + V 2 = 1 4 π ε 0 ( q r 1 − q r 2 ) = q ( r 2 − r 1 ) 4 π ε 0 r 1 r 2 V = V_1 + V_2 = \frac{1}{4\pi\varepsilon_0} \left( \frac{q}{r_1} - \frac{q}{r_2} \right) = \frac{q(r_2 - r_1)}{4\pi\varepsilon_0 r_1 r_2} V = V 1 + V 2 = 4 π ε 0 1 ( r 1 q − r 2 q ) = 4 π ε 0 r 1 r 2 q ( r 2 − r 1 ) 式中, r 1 r_1 r 1 r 2 r_2 r 2
设 r 为电偶极子中心到点 P 的径矢,则 θ \theta θ p e p_e p e r ≫ l r\gg l r ≫ l
r 2 − r 1 ≈ l cos θ ≈ r 1 r 2 ≈ r 2 r_2 - r_1 \approx l \cos \theta \approx r_1 r_2 \approx r^2 r 2 − r 1 ≈ l cos θ ≈ r 1 r 2 ≈ r 2 因此得 P 点电势
V ≈ q l cos θ 4 π ε 0 r 2 = p e cos θ 4 π ε 0 r 2 V \approx \frac{ql\cos\theta}{4\pi\varepsilon_0 r^2} = \frac{p_e\cos\theta}{4\pi\varepsilon_0 r^2} V ≈ 4 π ε 0 r 2 ql cos θ = 4 π ε 0 r 2 p e cos θ 例题 5-9
一均匀带电圆板,其电荷面密度为 σ \sigma σ
解:场源为连续带电体,先将其分割成若干同心圆环,参照图 5-26,每个圆环所带电荷量为 d q = σ 2 π r d r dq = \sigma 2\pi r dr d q = σ 2 π r d r 2 π r d r 2\pi r dr 2 π r d r r 2 + x 2 \sqrt{r^2+x^2} r 2 + x 2
d V = 1 4 π ε 0 σ 2 π r d r r 2 + x 2 dV = \frac{1}{4\pi\varepsilon_0} \frac{\sigma^2 \pi r dr}{\sqrt{r^2 + x^2}} d V = 4 π ε 0 1 r 2 + x 2 σ 2 π r d r
图 5-26 例题 5-9图
积分后得到整个带电圆板在 P 点的电势为
V = σ 2 π 4 π ε 0 ∫ 0 R r d r r 2 + x 2 = σ 2 ε 0 ( R 2 + x 2 − x ) V = \frac{\sigma 2\pi}{4\pi\varepsilon_0} \int_0^R \frac{r dr}{\sqrt{r^2 + x^2}} = \frac{\sigma}{2\varepsilon_0} (\sqrt{R^2 + x^2} - x) V = 4 π ε 0 σ 2 π ∫ 0 R r 2 + x 2 r d r = 2 ε 0 σ ( R 2 + x 2 − x ) 这一结果对轴线上各点都是正确的,在 x ≫ R x\gg R x ≫ R R 2 + x 2 \sqrt{R^2+x^2} R 2 + x 2
V ≈ σ 2 ε 0 ( x + R 2 2 x − x ) = σ R 2 π 4 π ε 0 x = q 4 π ε 0 x V \approx \frac{\sigma}{2\varepsilon_0} \left( x + \frac{R^2}{2x} - x \right) = \frac{\sigma R^2 \pi}{4\pi\varepsilon_0 x} = \frac{q}{4\pi\varepsilon_0 x} V ≈ 2 ε 0 σ ( x + 2 x R 2 − x ) = 4 π ε 0 x σ R 2 π = 4 π ε 0 x q 式中, q 为圆板带的总电荷量。
上式表明,圆板在远离它的空间(x≫R) 所产生的电势与一个电荷量相同的点电荷 所产生的电势相同。
例题 5-10
有一电荷线密度为 λ 的无限长均匀带电直线,如图 5-27 所示,试求它所产生的电势分布函数。
解:因为无限长带电直线场强的空间分布函数为 E = λ / ( 2 π ϵ 0 r ) E = \lambda/(2\pi\epsilon_0 r) E = λ / ( 2 π ϵ 0 r ) q 0 q_0 q 0 P 0 P_0 P 0 r 0 r_0 r 0
图 5-27 例题 5-10 图
V P ( r ) = ∫ P P 0 E ⋅ d l = ∫ r r 0 λ 2 π ε 0 r d r = λ 2 π ε 0 ln r 0 r V_{P}(r) = \int_{P}^{P_0} \mathbf{E} \cdot d\mathbf{l} = \int_{r}^{r_0} \frac{\lambda}{2\pi\varepsilon_0 r} dr = \frac{\lambda}{2\pi\varepsilon_0} \ln \frac{r_0}{r} V P ( r ) = ∫ P P 0 E ⋅ d l = ∫ r r 0 2 π ε 0 r λ d r = 2 π ε 0 λ ln r r 0 当 r > r 0 r > r_0 r > r 0 V p ( r ) < 0 V_p(r) < 0 V p ( r ) < 0 r 0 r_0 r 0
例题 5-11
如图 5-28 所示的一电偶极子,利用例题 5-8 得到的电势 V = p e cos θ 4 π ϵ 0 r 2 V = \frac{p_e \cos \theta}{4\pi\epsilon_0 r^2} V = 4 π ϵ 0 r 2 p e c o s θ
r = x 2 + y 2 r = \sqrt{x^2 + y^2} r = x 2 + y 2 , cos θ = x x 2 + y 2 \cos \theta = \frac{x}{\sqrt{x^2 + y^2}} cos θ = x 2 + y 2 x
V ( x , y ) = p e x 4 π ε 0 ( x 2 + y 2 ) 3 / 2 V(x,y) = \frac{p_e x}{4\pi\varepsilon_0 (x^2 + y^2)^{3/2}} V ( x , y ) = 4 π ε 0 ( x 2 + y 2 ) 3/2 p e x 于是,有
E x = − ∂ V ∂ x = p e ( 2 x 2 − y 2 ) 4 π ε 0 ( x 2 + y 2 ) 5 / 2 E_x = -\frac{\partial V}{\partial x} = \frac{p_e(2x^2 - y^2)}{4\pi\varepsilon_0(x^2 + y^2)^{5/2}} E x = − ∂ x ∂ V = 4 π ε 0 ( x 2 + y 2 ) 5/2 p e ( 2 x 2 − y 2 )
图 5-28 例题 5-11 图
E y = − ∂ V ∂ y = 3 p e x y 4 π ε 0 ( x 2 + y 2 ) 5 / 2 E_{y} = -\frac{\partial V}{\partial y} = \frac{3p_{e}xy}{4\pi\varepsilon_{0}(x^{2}+y^{2})^{5/2}} E y = − ∂ y ∂ V = 4 π ε 0 ( x 2 + y 2 ) 5/2 3 p e x y 若 P 点选在电偶极子轴线的中垂线(y 轴)上,即 x=0 时,
E = E x i = − P e 4 π ε 0 y 3 , E y = 0 E = E_x i = -\frac{P_e}{4\pi\varepsilon_0 y^3}, \quad E_y = 0 E = E x i = − 4 π ε 0 y 3 P e , E y = 0 式中,负号表示E与p。方向相反。
若P点选在电偶极子的延长线上,即y=0时,
E = E x i = p e 2 π ε 0 x 3 , E y = 0 E = E_x i = \frac{p_e}{2\pi\varepsilon_0 x^3}, \quad E_y = 0 E = E x i = 2 π ε 0 x 3 p e , E y = 0 对比 5.1.6 节中的讨论,可以看出,通过电势求电场强度,纯属标量运算,与矢量积分相比,计算过程要简单许多。