5.1.1 两种电荷
由分子组成的物质,其分子由原子组成,原子由原子核和核 外电子组成,原子核和电子都带电,但所带电的性质不同。规定 原子核所带的电荷为正;电子所带的电荷为负。正负电荷相互吸 引束缚在一起。通常情况下,原子中的正电荷数量与负电荷数量 相等,原子处于一种"电中性"状态。因此物体对外呈不带电现 象。如果通过外力将束缚在一起的两种电荷分离,并使物体所带 正负电荷中的一种减少或增加,物体就"带电"了,这种过程称为 起电。
最简单的起电方法是摩擦。摩擦后的琥珀、塑料、橡胶、丝 绸、毛发都具有明显的带电现象,其原因在于当两种性质不同的 物体相互接触并摩擦时,由于它们各自对核外电子吸引能力存在 差别,一个物体就会捕获另外物体上的电子,打破了物体原有的 电中性状态,于是两种物体分别带上了等量的正、负电荷。但是, 对于由这两种物质所组成的系统来说,摩擦前后正、负电荷的总 电荷量保持不变。如果将以上两个物体称为一个系统的话,则除 了这两个物体外都称之为外界。如果系统与外界既没有物质交 换,又没有能量交换,则称该系统为孤立系统。总结以上现象可 以得出:在孤立系统内无论进行什么过程,其电荷的代数和保持 不变,这称为电荷守恒定律。它是自然界的普遍规律之一。
△ 文档:库仑
文档:静电学的数学研究
文档:电荷与静电场
在经典物理中,电荷存在着一个最小的基本单元,这就是一个电子所带电荷量的绝对值。任何电荷所带电荷量q的绝对值只能是这个基本电荷单元的整数倍,即q=ne。这种现象称为电荷的量子化。式中,n为正整数,e为元电荷(一个电子电荷量的绝对值),近代物理给出其精确值为 1.602 176 620 8(98)× 10 − 19 10^{-19} 1 0 − 19 e = 1.6 × 10 − 19 e=1.6\times10^{-19} e = 1.6 × 1 0 − 19
1964 年,盖尔曼提出了强子由夸克组成的理论,并预言有多种夸克存在,它们所带的电荷分别为 + e 3 +\frac{e}{3} + 3 e − e 3 -\frac{e}{3} − 3 e + 2 e 3 +\frac{2e}{3} + 3 2 e − 2 e 3 -\frac{2e}{3} − 3 2 e
电荷还有一个重要的性质,即电荷的电荷量不会因为电荷的 运动状态而发生变化,电荷本身是一个相对性不变的量,在不同 参考系中,观测到的同样一个电荷所带电荷量一样。
5.1.2 库仑定律
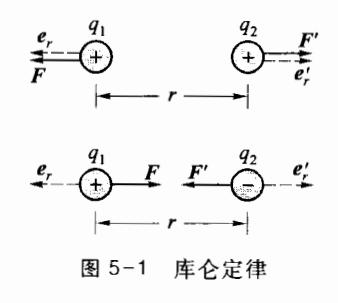
为了研究任意形状带电体之间的相互作用,1785 年库仑忽略了实际带电体的大小和形状,提出了点电荷模型,并给出了两个点电荷相互作用的规律,称为库仑定律,陈述如下(图 5-1):在真空中,电荷量为 q 1 q_1 q 1 q 2 q_2 q 2
F = K q 1 q 2 r 2 e r (5.1.1) F = K \frac{q_1 q_2}{r^2} e_r \tag{5.1.1} F = K r 2 q 1 q 2 e r ( 5.1.1 ) 式中, q 1 q_1 q 1 q 2 q_2 q 2 K = 1 / ( 4 π ε 0 ) = 8.9875 × 10 9 K=1/(4\pi\varepsilon_0)=8.9875\times10^9 K = 1/ ( 4 π ε 0 ) = 8.9875 × 1 0 9 ε 0 \varepsilon_0 ε 0 ε 0 = 8.85 × 10 − 12 \varepsilon_0=8.85\times10^{-12} ε 0 = 8.85 × 1 0 − 12 q 1 q_1 q 1
当空间有两个以上点电荷同时存在时,其中某一个电荷所受的力为其他每一个点电荷单独存在时,作用在该点电荷上力的矢量和.这种方法称为力的叠加原理。假设真空中存在 q 0 q_0 q 0 q 1 q_1 q 1 q 2 q_2 q 2 q 0 q_0 q 0
其他电荷的作用力为
F 0 = F 01 + F 02 + F 03 + ⋯ \boldsymbol{F}_{0} = \boldsymbol{F}_{01} + \boldsymbol{F}_{02} + \boldsymbol{F}_{03} + \cdots F 0 = F 01 + F 02 + F 03 + ⋯ (5.1.2)
式中, F 01 F_{01} F 01 F 02 F_{02} F 02 F 03 F_{03} F 03 q 1 q_1 q 1 q 2 q_2 q 2 q 3 q_3 q 3 q 0 q_0 q 0
在以上讨论中我们注意到,电荷之间的作用力无须它们之间相互接触就能实现,那么电荷间的作用力是怎样实现的呢?
5.1.3 真空中的静电场
科学的发展已经证明,电荷周围存在着电场,电荷之间通过 电场发生相互作用,作用方式为
即电荷 q 1 q_1 q 1 q 2 q_2 q 2 q 2 q_2 q 2 q 1 q_1 q 1
为了研究 q 在空间某点 P 处的电场强度,通常选用检验电荷 q 0 q_0 q 0 q 0 q_0 q 0 q 0 q_0 q 0 q 0 q_0 q 0 q 0 q_0 q 0 q 0 q_0 q 0 q 0 q_0 q 0 q 0 q_0 q 0 F / q 0 F/q_0 F / q 0
E = F / q 0 (5.1.3) \boldsymbol{E} = \boldsymbol{F}/q_0 \tag{5.1.3} E = F / q 0 ( 5.1.3 ) 式中,E 为电场强度(以下简称场强)。由定义式(5.1.3)可知,电场中某点的场强 E,在数值上等于单位检测电荷在该点处所受到的电场力,场强 E 的方向规定为正电荷在该点所受电场力的方向。一般说,E 是空间位置的函数,如在某个区域 E 保持不变,则称该电场为均匀电场。在国际单位制中,场强 E 的单位是 N ⋅ C − 1 N\cdot C^{-1} N ⋅ C − 1 V ⋅ m − 1 V\cdot m^{-1} V ⋅ m − 1
5.1.4 场强叠加原理
图 5-2 场强的叠加原理
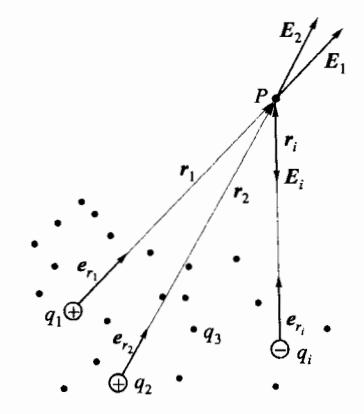
由式(5.1.2)已知,空间某电荷 q 0 q_0 q 0 q 0 q_0 q 0 q 0 q_0 q 0 q 0 q_0 q 0
E = E 1 + E 2 + ⋯ + E n = ∑ i = 1 n E i E = E_1 + E_2 + \dots + E_n = \sum_{i=1}^n E_i E = E 1 + E 2 + ⋯ + E n = i = 1 ∑ n E i (5.1.4)
上式说明,电场中任意点 P 的场强,等于空间各点电荷单独 在该点产生场强的矢量和,如图 5-2 所示。这就是场强叠加原 理,它是电场的重要性质,也是物理学中的基本原理。
5.1.5 电场强度的计算
当电荷的空间分布确定以后,从场强的定义式出发,利用场强叠加原理,就可以求出场强的空间分布。下面讨论场强的计算方法。
1. 点电荷的场强
利用库仑定律和场强定义式计算。如图 5-3 所示,真空中某一位置有一点电荷 q,为了确定它在空间任意点 P 产生的场强,从 q 向 P 点引一径矢 r,以表明场点的位置。设想在 P 点处有一个检验电荷 q 0 q_0 q 0 q 0 q_0 q 0
F = K q q 0 r 2 e r F = K \frac{qq_0}{r^2} e_r F = K r 2 q q 0 e r 由场强定义式(5.1.3)可得到点电荷 q 在 P 点产生的场强为
E = K q r 2 e r ( 5.1.5 ) E = K \frac{q}{r^2} e_r \qquad (5.1.5) E = K r 2 q e r ( 5.1.5 ) 式中,e,表示由 q 指向场点 P 的单位矢量。
由式(5.1.5)可以得知,在点电荷电场中,场点 P 处的场强大小与产生该电场的电荷 q 的电荷量成正比;与从 q 到 P 处距离的平方成反比。场强方向与 q 的电性质有关,当 q 为正电荷时,场强 E 与 e, 同向,指向背离 q 的方向;若 q 为负电荷,则场强 E 与 e, 反向,指向 q 的方向。
值得注意的是,式(5.1.5)是一个位置函数表达式,它给出了点电荷 q 周围任意点的场强。式(5.1.5)是一个重要的表达式,以它为基础,原则上可以计算出任何带电体在空间产生的场
图 5-3 点电荷的场强
强分布。
2. 点电荷系的场强
如图 5-4 所示,空间分布着 n 个点电荷 q 1 , q 2 , … , q n q_1, q_2, \dots, q_n q 1 , q 2 , … , q n E i = K q i r i 2 e r i E_i = K \frac{q_i}{r_i^2} e_{r_i} E i = K r i 2 q i e r i
E = E 1 + E 2 + ⋯ + E n = K q 1 r 1 2 e r 1 + K q 2 r 2 2 e r 2 + ⋯ + K q n r n 2 e r n = ∑ i = 1 n K q i r i 2 e r i ( 5.1.6 ) E = E_{1} + E_{2} + \dots + E_{n} = K \frac{q_{1}}{r_{1}^{2}} e_{r_{1}} + K \frac{q_{2}}{r_{2}^{2}} e_{r_{2}} + \dots + K \frac{q_{n}}{r_{n}^{2}} e_{r_{n}} = \sum_{i=1}^{n} K \frac{q_{i}}{r_{i}^{2}} e_{r_{i}} \quad (5.1.6) E = E 1 + E 2 + ⋯ + E n = K r 1 2 q 1 e r 1 + K r 2 2 q 2 e r 2 + ⋯ + K r n 2 q n e r n = i = 1 ∑ n K r i 2 q i e r i ( 5.1.6 ) 由式(5.1.6)可以看出,场强的叠加原理反映了点电荷在空间产生的场强的独立性。一个电荷在某点产生的场强,其大小和方向并不因为其他电荷的存在而发生变化。
3. 连续带电体的场强
如果电荷连续地分布在某一个具有一定形状的物体上,则称该物体为连续带电体。求解连续带电体产生的场强分布,依然依据场强的叠加原理。此时,先要将带电体分割成大量足够小的电荷元 dq,每个电荷元都可以视为一个点电荷。任意一个电荷元 dq 在空间某点 P 产生的场强为
d E = 1 4 π ε 0 d q r 2 e r , K = 1 4 π ε 0 dE = \frac{1}{4\pi\varepsilon_0} \frac{dq}{r^2} e_r, \quad K = \frac{1}{4\pi\varepsilon_0} d E = 4 π ε 0 1 r 2 d q e r , K = 4 π ε 0 1 (5.1.7)
式中,r 为电荷元 dq 到点 P 的距离,e, 为 dq 指向场点的单位矢量。依场强叠加原理,整个带电体在点 P 所产生的总场强为
E = ∫ d E = ∫ 1 4 π ε 0 d q r 2 E = \int dE = \int \frac{1}{4\pi\varepsilon_0} \frac{dq}{r^2} E = ∫ d E = ∫ 4 π ε 0 1 r 2 d q (5.1.8)
积分遍布整个带电体。
具体说来,电荷可能分布在某种形状的曲线、曲面或三维物体上,为了完成积分,需要引入电荷密度的概念,定义 λ \lambda λ σ \sigma σ ρ \rho ρ d q = λ d l \mathrm{d}q = \lambda\,\mathrm{d}l d q = λ d l d q = σ d S \mathrm{d}q = \sigma\,\mathrm{d}S d q = σ d S d q = ρ d V \mathrm{d}q = \rho\,\mathrm{d}V d q = ρ d V d l \mathrm{d}l d l d S \mathrm{d}S d S d V \mathrm{d}V d V
E = 1 4 π ε 0 ∮ l λ d l r 2 e r E = \frac{1}{4\pi\varepsilon_0} \oint_l \frac{\lambda \, dl}{r^2} \boldsymbol{e}_r E = 4 π ε 0 1 ∮ l r 2 λ d l e r E = 1 4 π ε 0 ∮ S σ d S r 2 e r E = \frac{1}{4\pi\varepsilon_0} \oint_S \frac{\sigma \, dS}{r^2} \boldsymbol{e}_r E = 4 π ε 0 1 ∮ S r 2 σ d S e r
图 5-4 点电荷系的场强
E = 1 4 π ε 0 ∫ V ρ d V r 2 e r E = \frac{1}{4\pi\varepsilon_0} \int_V \frac{\rho \, \mathrm{d}V}{r^2} e_r E = 4 π ε 0 1 ∫ V r 2 ρ d V e r 上面诸式是矢量积分,一般情况下积分式中的 λ \lambda λ σ \sigma σ ρ \rho ρ λ \lambda λ σ \sigma σ ρ \rho ρ
E x = ∫ d E x E_x = \int dE_x E x = ∫ d E x , E y = ∫ d E y E_y = \int dE_y E y = ∫ d E y E z = ∫ d E z E_z = \int dE_z E z = ∫ d E z
因此可得到电场强度的空间分布为
E = E x i + E x j + E z k E = E_x i + E_x j + E_z k E = E x i + E x j + E z k 由上式可知,只要已知电荷分布,原则上就可以由点电荷场强公式及场强叠加原理求出电场中任意点的场强。
在下文中,利用上述求场强的方法,分析电偶极子在空间产生的场强,及电偶极子在外电场中所受的力和力矩。
5.1.6 电偶极子模型
如图 5-5 所示,相隔距离 l、束缚在一起的两个等量异号点电荷,当它们的中心到所考虑点 P 的距离 r 比这对点电荷间的距离 l 大得多时,即 r ≫ l r\gg l r ≫ l p e p_e p e p e = q l o p_e=ql_o p e = q l o p e p_e p e p e p_e p e
(1) 电偶极子在其延长线上一点处的场强
如图 5-6 所示,设 O 点为电偶极子轴线的中心,并设 O 点到点 P 的距离为 r,即 OP=r,则 t0 电荷在 t7 点的场强分别为
E + = K q r + 2 e r + = K q ( r − l / 2 ) 2 e r + E_{+} = K \frac{q}{r_{+}^{2}} e_{r_{+}} = K \frac{q}{(r-l/2)^{2}} e_{r_{+}} E + = K r + 2 q e r + = K ( r − l /2 ) 2 q e r + E − = K ( − q ) r − 2 e r − = K ( − q ) ( r + l / 2 ) 2 e r − E_{-} = K \frac{(-q)}{r_{-}^{2}} e_{r_{-}} = K \frac{(-q)}{(r+l/2)^{2}} e_{r_{-}} E − = K r − 2 ( − q ) e r − = K ( r + l /2 ) 2 ( − q ) e r − 依据场强的叠加原理,有
图 5-6 电偶极子在轴线处的场强
E p = K q [ 1 ( r − l / 2 ) 2 − 1 ( r + l / 2 ) 2 ] e r E_p = Kq \left[ \frac{1}{(r-l/2)^2} - \frac{1}{(r+l/2)^2} \right] e_r E p = K q [ ( r − l /2 ) 2 1 − ( r + l /2 ) 2 1 ] e r 考虑到 r ≫ l r\gg l r ≫ l p e = q l p_e=ql p e = ql K = 1 / ( 4 π ε 0 ) K=1/(4\pi\varepsilon_0) K = 1/ ( 4 π ε 0 )
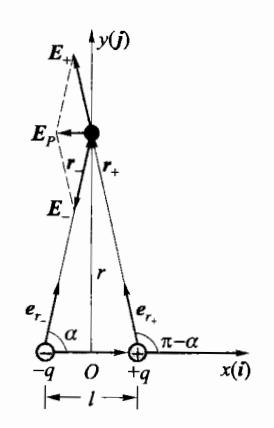
E P ≈ 2 p e 4 π ε 0 r 3 = p e 2 π ε 0 r 3 (5.1.9) E_P \approx \frac{2\boldsymbol{p}_e}{4\pi\varepsilon_0 r^3} = \frac{\boldsymbol{p}_e}{2\pi\varepsilon_0 r^3} \tag{5.1.9} E P ≈ 4 π ε 0 r 3 2 p e = 2 π ε 0 r 3 p e ( 5.1.9 ) (2) 电偶极子轴线中垂面上某点 P 处的场强(图 5-7)为 E o = E o + E o E_{o}=E_{o}+E_{o} E o = E o + E o
而
E + = K q r + 2 e r + = K q r 2 + ( l / 2 ) 2 ( − cos α i + sin α j ) E_{+} = K \frac{q}{r_{+}^{2}} e_{r_{+}} = K \frac{q}{r^{2} + (l/2)^{2}} (-\cos \alpha \mathbf{i} + \sin \alpha \mathbf{j}) E + = K r + 2 q e r + = K r 2 + ( l /2 ) 2 q ( − cos α i + sin α j ) E − = K − q r − 2 e r − = K q r 2 + ( l / 2 ) 2 ( − cos α i − sin α j ) E_{-} = K \frac{-q}{r_{-}^{2}} e_{r_{-}} = K \frac{q}{r^{2} + (l/2)^{2}} (-\cos \alpha \mathbf{i} - \sin \alpha \mathbf{j}) E − = K r − 2 − q e r − = K r 2 + ( l /2 ) 2 q ( − cos α i − sin α j ) 所以
E p = K q r 2 + ( l / 2 ) 2 ( − 2 cos α ) i E_{p} = K \frac{q}{r^{2} + (l/2)^{2}} (-2\cos \alpha) \mathbf{i} E p = K r 2 + ( l /2 ) 2 q ( − 2 cos α ) i 而 cos α = l / 2 r 2 + ( l / 2 ) 2 \cos \alpha = \frac{l/2}{\sqrt{r^2 + (l/2)^2}} cos α = r 2 + ( l /2 ) 2 l /2 r ≫ l r \gg l r ≫ l p e = q l p_e = ql p e = ql
E P ≈ − p e 4 π ε 0 r 3 \boldsymbol{E}_{P} \approx -\frac{\boldsymbol{p}_{e}}{4\pi\varepsilon_{0}r^{3}} E P ≈ − 4 π ε 0 r 3 p e 其数值可以写为
E P = − P e 4 π ε 0 r 3 (5.1.10) E_P = -\frac{P_e}{4\pi\varepsilon_0 r^3} \tag{5.1.10} E P = − 4 π ε 0 r 3 P e ( 5.1.10 ) 电偶极子是一个很有用的模型,在此后讨论到电介质极化问题时可知,极化后的分子或原子都可以看成电偶极子,发射电磁波的天线也可以被视为振荡的电偶极子。
2. 电偶极子在均匀外场中所受的力和力矩
如图 5-8(a)所示,电偶极子位于场强为 E 的均匀外电场中。 E 与电矩 p e p_e p e θ \theta θ F + F_+ F + F − F_- F − F + F_+ F + F − F_- F − ∑ F = 0 \sum F=0 ∑ F = 0 M = q E l sin θ M=qEl\sin\theta M = qEl sin θ q l = p e ql=p_e ql = p e M = p e E sin θ M=p_eE\sin\theta M = p e E sin θ p e p_e p e
M = p × E (5.1.11) \mathbf{M} = \mathbf{p} \times \mathbf{E} \tag{5.1.11} M = p × E ( 5.1.11 ) 电偶极子在该力矩的作用下,使 p e p_e p e
图 5-7 电偶极子中垂面上某点 的场强
图 5-8 电偶极子在均匀外电场 中的力矩
例题 5-1
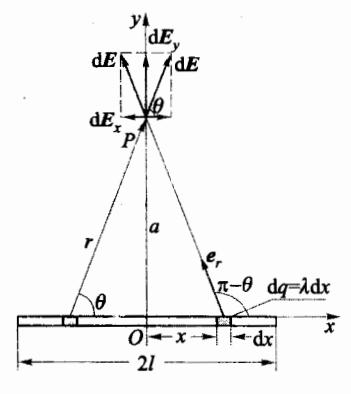
如图所示,一段直线形物体均匀带电,求其中垂面上某点处的电场强度。假设这段带电直线长为 2l ,所带电荷量为 g 。
解:如图 5-9 所示,选取直角坐标系,带电直线与x 轴重合,y 轴与带电直线垂直,坐标原点选在这段直线的中点。
在带电线任意位置处选一电荷元 d q = λ d x dq = \lambda dx d q = λ d x λ = q / ( 2 l ) \lambda = q/(2l) λ = q / ( 2 l )
d E = 1 4 π ε 0 λ d x r 2 e r \mathrm{d}\boldsymbol{E} = \frac{1}{4\pi\varepsilon_0} \frac{\lambda \,\mathrm{d}x}{r^2} \boldsymbol{e}_r d E = 4 π ε 0 1 r 2 λ d x e r 式中,r为 dq 到 P 的距离,e, 为单位矢量。 设点 P 到带电线的距离为 a,则 r 2 = a 2 + x 2 r^2 = a^2 + x^2 r 2 = a 2 + x 2 cos ( π − θ ) i + sin θ j \cos(\pi - \theta)i + \sin\theta j cos ( π − θ ) i + sin θ j
d E = 1 4 π ε 0 λ d x x 2 + a 2 ( − cos θ i + sin θ j ) dE = \frac{1}{4\pi\varepsilon_0} \frac{\lambda dx}{x^2 + a^2} (-\cos\theta i + \sin\theta j) d E = 4 π ε 0 1 x 2 + a 2 λ d x ( − cos θ i + sin θ j ) 它在x轴、y轴上的分量的数值为
d E x = 1 4 π ε 0 λ d x x 2 + a 2 cos θ , dE_x = \frac{1}{4\pi\varepsilon_0} \frac{\lambda dx}{x^2 + a^2} \cos \theta, d E x = 4 π ε 0 1 x 2 + a 2 λ d x cos θ , ≠ cos θ = x x 2 + a 2 \neq \cos \theta = \frac{x}{\sqrt{x^2 + a^2}} = cos θ = x 2 + a 2 x dEy =
1 4 π ε 0 λ d x x 2 + a 2 sin θ \frac{1}{4\pi\varepsilon_0} \frac{\lambda dx}{x^2 + a^2} \sin \theta 4 π ε 0 1 x 2 + a 2 λ d x sin θ , 其中 sin θ = a x 2 + a 2 \theta = \frac{a}{\sqrt{x^2 + a^2}} θ = x 2 + a 2 a
考虑到整根带电线对于坐标原点具有对称性,所以全部电荷元在P点场强沿z方向的分量之和为零,P点处的总场强只沿y轴方向,即
图 5-9 例题 5-1图
E = E y = ∫ d E y = ∫ − l l a λ d x 4 π ε 0 ( x 2 + a 2 ) 3 / 2 E = E_{y} = \int dE_{y} = \int_{-l}^{l} \frac{a\lambda dx}{4\pi\varepsilon_{0}(x^{2} + a^{2})^{3/2}} E = E y = ∫ d E y = ∫ − l l 4 π ε 0 ( x 2 + a 2 ) 3/2 aλ d x = λ l 2 π ε 0 a a 2 + l 2 = \frac{\lambda l}{2\pi\varepsilon_{0}a\sqrt{a^{2} + l^{2}}} = 2 π ε 0 a a 2 + l 2 λ l 当直线所带电荷为正时,E 指向远离带电线的方向。
当带电线的长度远大于点 P 与带电线间的距离时(即 l ≫ a l\gg a l ≫ a
E = λ 2 π ε 0 a E = \frac{\lambda}{2\pi\varepsilon_0 a} E = 2 π ε 0 a λ 方向垂直于带电直线,当所带为正电荷时, 电场指向远离带电直线的方向;当所带为负 电荷时,电场指向带电直线。
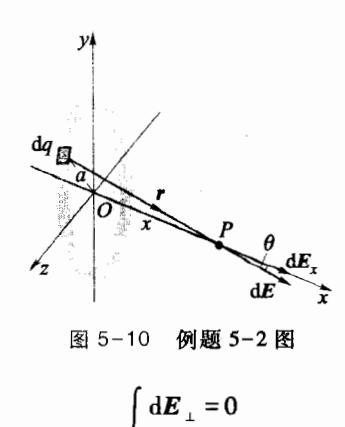
例题 5-2
计算一均匀带电细圆环轴线上某点处的场强。设圆环的半径为 a, 所带电荷量为 q。
解:如图 5-10 所示,建立一空间直角坐标系,并使带电圆环位于 yz 平面上,圆心位于 坐标原点。带电圆环上任意取一电荷元 dq 在 x 轴上 P 点处的场强为 dE, dE 可以分解
成平行于x轴的分量 d E x E_x E x E ⊥ E_\perp E ⊥
因此整个带电圆环在轴线任意点处的 场强方向都与x轴平行(或反向平行)。当圆
环带正电荷时,场强沿x轴方向;当圆环带负电荷时,场强方向与x轴方向相反。因此
E = E x = ∫ d E x = ∫ 0 2 π a 1 4 π ε 0 λ d l ( a 2 + x 2 ) cos θ E = E_x = \int dE_x = \int_0^{2\pi a} \frac{1}{4\pi\varepsilon_0} \frac{\lambda dl}{(a^2 + x^2)} \cos \theta E = E x = ∫ d E x = ∫ 0 2 πa 4 π ε 0 1 ( a 2 + x 2 ) λ d l cos θ 式中,
cos θ = x a 2 + x 2 \cos \theta = \frac{x}{\sqrt{a^2 + x^2}} cos θ = a 2 + x 2 x 。 所以
E = ∫ 0 2 π a 1 4 π ε 0 x λ d l ( a 2 + x 2 ) 3 / 2 = x λ 2 π a 4 π ε 0 ( a 2 + x 2 ) 3 / 2 = q x 4 π ε 0 ( a 2 + x 2 ) 3 / 2 E = \int_0^{2\pi a} \frac{1}{4\pi\varepsilon_0} \frac{x\lambda \, dl}{(a^2 + x^2)^{3/2}} = \frac{x\lambda 2\pi a}{4\pi\varepsilon_0 (a^2 + x^2)^{3/2}} \\ = \frac{qx}{4\pi\varepsilon_0 (a^2 + x^2)^{3/2}} E = ∫ 0 2 πa 4 π ε 0 1 ( a 2 + x 2 ) 3/2 x λ d l = 4 π ε 0 ( a 2 + x 2 ) 3/2 x λ 2 πa = 4 π ε 0 ( a 2 + x 2 ) 3/2 q x 例题 5-3
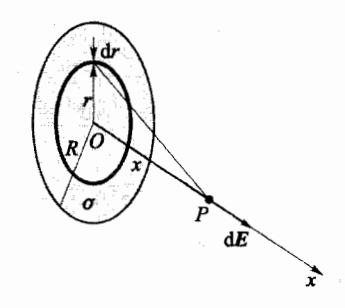
计算一均匀带电薄圆盘,在垂直通过其圆心的轴线上,任意点处的场强。设圆盘半径为R,电荷面密度为 σ \sigma σ
解:如图 5-11 所示,可将带电圆盘视为由许多带电的同心圆环组成,取其中任意带电环,该圆环半径为r,宽度为 dr,则该圆环所带电荷量为 d q = σ 2 π r d r dq = \sigma 2\pi r dr d q = σ 2 π r d r d E = σ 2 π r x d r 4 π ε 0 ( r 2 + x 2 ) 3 / 2 dE = \frac{\sigma 2\pi r x dr}{4\pi \varepsilon_0 (r^2 + x^2)^{3/2}} d E = 4 π ε 0 ( r 2 + x 2 ) 3/2 σ 2 π r x d r
图 5-11 例题 5-3图
度方向与x轴反向)。整个圆盘在P点的场强大小是所有带电细环在P点场强之和,即
E = ∫ d E = σ x 2 ε 0 ∫ 0 R r d r ( r 2 + x 2 ) 3 / 2 E = \int dE = \frac{\sigma x}{2\varepsilon_0} \int_0^R \frac{r dr}{(r^2 + x^2)^{3/2}} E = ∫ d E = 2 ε 0 σ x ∫ 0 R ( r 2 + x 2 ) 3/2 r d r = σ 2 ε 0 ( 1 − x R 2 + x 2 ) = \frac{\sigma}{2\varepsilon_0} \left( 1 - \frac{x}{\sqrt{R^2 + x^2}} \right) = 2 ε 0 σ ( 1 − R 2 + x 2 x ) 讨论两种特殊情况:
(1) 当 x ≪ R x \ll R x ≪ R E = σ 2 ε 0 E = \frac{\sigma}{2\varepsilon_0} E = 2 ε 0 σ
(2) 当
x ≫ R x\gg R x ≫ R 时, E ≈ π R 2 σ 4 π ε 0 x 2 = q 4 π ε 0 x 2 E\approx \frac{\pi R^2\sigma}{4\pi\varepsilon_0x^2} = \frac{q}{4\pi\varepsilon_0x^2} E ≈ 4 π ε 0 x 2 π R 2 σ = 4 π ε 0 x 2 q