4.7 熵

热力学第二定律说明了实际存在的自发过程都是有方向性的,这显示出自发过程(或不可逆过程)的初态和终态之间存在着重大差别,正是这种差异决定了过程进行的方向。为了描述这种差异,人们引入了态函数熵。

文档:熵 熵增原理

4.7.1 熵的引入

由卡诺定理(1),即 $\eta_{\neg i} = 1 - \frac{|Q_2|}{Q_1} = 1 - \frac{T_2}{T_1}$ ,注意到放出热量 $Q_2 < 0$ ,该式可写成

$$\frac{Q_1}{T_1} + \frac{Q_2}{T_2} = 0 (4.7.1)$$

卡诺循环由两个等温过程和两个绝热过程组成,在绝热过程中, $\frac{Q}{T}$ =0,因此式(4.7.1)表明在整个可逆卡诺循环中, $\frac{Q}{T}$ 的总和为零。

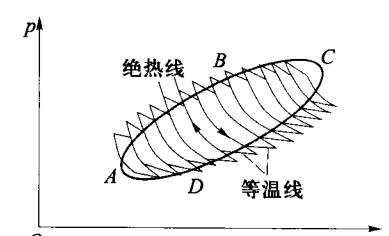
上述结论可推广至任意的可逆循环过程。图 4-19 中的闭合 曲线 ABCDA 表示一个任意的可逆循环过程。设计一系列如图所 示的紧密连接的微小的可逆卡诺循环,因为两个相邻的卡诺循环 o 共用一条绝热线,而绝热过程进行的方向相反,因而效果抵消。

图 4-19 任意可逆循环过程

因此这些小循环的总效果相当于图中锯齿形的闭合曲线。对于 其中每一小循环均有

$$\frac{\Delta Q_{i1}}{T_{i1}} + \frac{\Delta Q_{i2}}{T_{i2}} = 0$$

上式对所有小卡诺循环求和,则有

$$\sum \frac{\Delta Q_i}{T_i} = 0$$

如果小卡诺循环的数目趋向无穷大,各小段的等温线长度将趋于零,锯齿形曲线则会与实际的循环过程曲线重合。上式的求和转化为沿闭合曲线 ABCDA 的积分:

$$\oint \frac{\mathrm{d}Q}{T} = 0$$

(4.7.2)

式中,dQ 为系统在一无限小等温过程中,与温度为 T 的热源交换的热量, $\oint$ 表示积分沿 ABCDA 整个可逆循环过程进行。

图 4-19 所示的循环过程可认为是由 ABC 和 CDA 两个可逆过程构成,因此式(4.7.2)可改写为

$$\oint \frac{\mathrm{d}Q}{T} = \int_{ABC} \frac{\mathrm{d}Q}{T} + \int_{CDA} \frac{\mathrm{d}Q}{T} = 0$$

考虑到过程是可逆的,上式可写为

$$\int_{ABC} \frac{\mathrm{d}Q}{T} - \int_{ADC} \frac{\mathrm{d}Q}{T} = 0$$

或

$$\int_{ABC} \frac{\mathrm{d}Q}{T} = \int_{ABC} \frac{\mathrm{d}Q}{T} \tag{4.7.3}$$

由于图示过程为任意的可逆过程,这就表明 $\int_A^c \frac{\mathrm{d}Q}{T}$ 的值只由始、末平衡态决定,而与具体的可逆过程无关,对于连接 A 和 C 两状态间的所有可逆过程, $\frac{\mathrm{d}Q}{T}$ 的积分有着相同的值。据此,我们可定义一个态函数,称为熵,用符号 S 表示。系统由初态 A 变化到终态 C 时熵的增量定义为

$$\Delta S = S_c - S_A = \int_{A(\vec{\eta};\underline{w})}^{c} \frac{\mathrm{d}Q}{T}$$

(4.7.4)

式中, $S_A$ 和 $S_c$ 分别是初态 A 和末态 C 的熵。在国际单位制中,熵的单位是 $\mathbf{J} \cdot \mathbf{K}^{-1}$ (焦耳每开尔文)。

熵是系统状态的单值函数,只要系统状态确定,熵就确定。 所以,当系统从初态变化到终态时,不论经历的是怎样的过程,也

不论过程是否可逆,熵的变化是一定的。

对于一个无限小的可逆过程,则有

$$dS = \left(\frac{dQ}{T}\right)_{\text{of } \underline{w}} \tag{4.7.5}$$

4.7.2 熵增加原理

由卡诺定理(2),可以得出在不可逆循环过程中,有

$$\oint \frac{\mathrm{d}Q}{T} < 0$$

(4.7.6)

假设某循环过程由一个不可逆过程 I 和一个可逆过程 II 构成,如图 4-20 所示,因为含有不可逆的中间过程,所以整个循环是一个不可逆的循环过程。对整个过程,有

$$\int_{A(\pi\ni\check{\varpi})}^{B}\frac{\mathrm{d}Q}{T}+\int_{B(\ni\check{\varpi})}^{A}\frac{\mathrm{d}Q}{T}\!<\!0$$

考虑到其中的可逆过程,上式改写为

$$\int_{A(\pi \cap \check{\mathbb{Z}})}^{B} \frac{\mathrm{d}Q}{T} - \int_{A(\pi \check{\mathbb{Z}})}^{B} \frac{\mathrm{d}Q}{T} < 0$$

或

$$\int_{A(\vec{n}\vec{w})}^{B} \frac{\mathrm{d}Q}{T} > \int_{A(\vec{n}\vec{w})}^{B} \frac{\mathrm{d}Q}{T}$$

将可逆过程中 $\Delta S = S_B - S_A = \int_{A(\Pi, \Psi)}^B \frac{dQ}{T}$ 代人上式,有

$$\Delta S > \int_{A(\pi, \overline{\eta}, \hat{\mathbf{w}})}^{B} \frac{\mathrm{d}Q}{T} \tag{4.7.7}$$

即在任意不可逆过程中, $\frac{dQ}{T}$ 的积分小于过程始末的熵增。对于无限小不可逆过程,有

$$\frac{\mathrm{d}Q}{T} < \mathrm{d}S \tag{4.7.8}$$

将可逆过程与不可逆过程归纳在一起考虑,则熵变为

$$\Delta S \geqslant \int_{A}^{B} \frac{\mathrm{d}Q}{T} \tag{4.7.9}$$

对微小的热力学过程,有

$$dS \geqslant \frac{dQ}{T} \tag{4.7.10}$$

上述两式中的"="对应于可逆过程,而">"对应于不可逆过程。 当 dQ=0 时,由上式得

图 4-20 不可逆循环过程

(4.7.11)

这表明,系统经绝热过程熵不会减小,对于可逆绝热过程,熵不变,对于不可逆绝热过程,熵增加,这一结论称为熵增加原理。

对于不受外界影响的孤立系统,总会有 dQ = 0,因此得到熵增加原理的另一种表述:一个孤立系统的熵永不减少。孤立系统总是自发地由非平衡态向平衡态转变,到达平衡状态时,系统的熵达到最大值。

4.7.3 熵的微观意义

在前面讨论热力学第二定律时,我们知道,一个实际的热力学系统总是由出现概率小的宏观态向着出现概率大的宏观态转变,由包含微观状态数少的宏观态向着包含微观状态数多的宏观态转变。而由熵增加原理,不受外界影响的热力学系统总是自发地向着熵增加的方向转变。显然,态函数熵与热力学概率间,或与微观状态数间必有某种联系。在统计物理学中可以证明,熵S与系统微观状态数 $\Omega$ 间存在如下关系:

$$S = k \ln \Omega \tag{4.7.12}$$

这一关系称为玻耳兹曼关系,其中 k 是玻耳兹曼常量。该式表明,对于给定的热力学系统,其包括的微观状态数目越多,组成系统的分子无规则热运动的无序性就越大,则熵值越大,这正是熵的微观解释。所以,熵是系统内部分子热运动无序程度的量度。

例题 4-8

质量为 m 的某理想气体由初始状态 $(p_0, V_0, T_0)$ 经绝热自由膨胀变到末态 $(p, 2V_0, T)$ ,求过程前后系统的熵增。

解:理想气体在绝热自由膨胀过程中,吸热、做功均为 0,所以气体内能不变,因此始末态的温度相等,即 $T=T_0$ ,因此有 $p=p_0/2$ 。

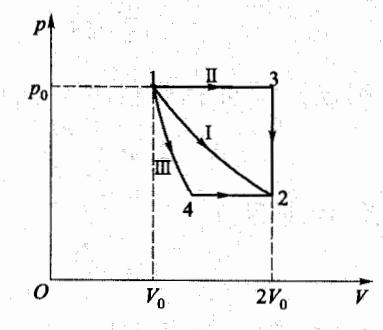
因为理想气体的绝热自由膨胀过程为不可逆过程,但熵为态函数,所以我们可以设计可逆过程连接始末状态,借助可逆过程计算熵增。下面我们以如图 4-21 所示的三条路径(路径 I:1→2 的等温过程;路径 II:

图 4-21 例题 4-8 图

1→3 的等压过程和 3→2 等体过程;路径 II:1→4 的绝热过程和 4→2 等压过程)为例,分别计算过程前后的熵增,比较其结果。

$$\Delta S = \int_{1}^{2} \frac{dQ}{T} = \frac{1}{T_{0}} \int_{1}^{2} dQ = \frac{1}{T_{0}} \frac{m}{M} R T_{0} \ln \frac{V_{2}}{V_{1}}$$ $$= R \frac{m}{M} \ln \frac{2V_{0}}{V_{0}} = \frac{m}{M} R \ln 2$$ $$\Delta S = \Delta S_{13} + \Delta S_{32} = \int_{1}^{3} \frac{dQ}{T} + \int_{3}^{2} \frac{dQ}{T}$$ $$= \int_{1}^{3} \frac{1}{T} \frac{m}{M} C_{p, m} dT + \int_{3}^{2} \frac{1}{T} \frac{m}{M} C_{v, m} dT$$ $$= \frac{m}{M} C_{p, m} \ln \frac{T_{3}}{T_{1}} + \frac{m}{M} C_{v, m} \ln \frac{T_{2}}{T_{3}}$$

而

$$T_1 = T_2 = T_0$$

, $T_3 = 2T_1 = 2T_0$ , 所以

$$\Delta S = \frac{m}{M} \ln 2(C_{p,m} - C_{v,m}) = \frac{m}{M} R \ln 2$$

(3) 1→4→2 过程

$$\Delta S = \Delta S_{14} + \Delta S_{42} = 0 + \int_{4}^{2} \frac{dQ}{T} = \int_{4}^{2} \frac{1}{T} \frac{m}{M} C_{p, m} dT$$ $$= \frac{m}{M} C_{p, m} \ln \frac{T_{2}}{T_{4}} = \frac{m}{M} C_{p, m} \ln \frac{T_{1}}{T_{4}}$$

由准静态绝热过程方程 $p^{\gamma-1}T^{-\gamma}=常量,得$

$$\frac{T_1}{T_4} = \left(\frac{p_1}{p_4}\right)^{\frac{\gamma-1}{\gamma}}$$

所以

$$\Delta S = \frac{m}{M} C_{p, m} \frac{\gamma - 1}{\gamma} \ln \frac{p_1}{p_4} = \frac{m}{M} R \ln 2$$

可见,三种过程 $(1\rightarrow 2,1\rightarrow 3\rightarrow 2$ 和 $1\rightarrow 4$ $\rightarrow 2$ ) 前后系统熵增相等,与熵为态函数相对应;另外可以看出,熵增为正值,即理想气体经绝热自由膨胀后熵增加,这与该绝热过程的不可逆性相对应。

思考题与习题

• 4.1 下述说法是否正确。
• (1) 理想气体吸收热量时,温度必然升高,而放出 热量时,温度一定降低。
• (2) 只要过程的初、末状态相同,无论经历什么样的准静态过程,一定有0-W 保持不变。
• 4.2 理想气体由平衡态 A 出发,经历某热力学过程到达另一平衡态 B, 若经历的分别是: 准静态过程 I 和非准静态过程 II。则二过程中气体所做的功、吸收的热量和内能变化是否均相同?
  • 4.3 下述为热力学第一定律的两种表述: Q=ΔE+W

及

$$\int \frac{m}{M} C_{m} dT = \frac{m}{M} C_{V_{m}} (T_{2} - T_{1}) + \int p dV$$

二者的适用条件有何不同?

4.4 一定量的理想气体由平衡态 A 出发,经历三个不同的准静态过程到达另一个平衡态 B,如图所示。若要求过程中气体做功:(1)为正;(2)为负;(3)为零。在图上画出三个相应的过程曲线。

4.5 一定量的理想气体由平衡态 $A(p_1, V_1, T)$ 经过一准静态过程达到另一平衡态 $B(p_2, V_2, T)$ ,能说该热力学过程是等温过程吗?请举例说明。

4.6 如图所示为一理想气体的准静态过程曲 4.9 两条绝 线,从图中可断定系统做功大于零、吸收热量及内能 环过程?为什么?增加,这种论断有无错误?

4.7 一定量的理想气体经历如图所示的三个不同过程,哪一个是吸热过程?哪一个是放热过程?其中 $1\rightarrow 2$ 为绝热线。

4.8 如图所示,一定量的某理想气体所做的两个卡诺循环在不同的高温线上,但循环曲线 ABCDA 和 A'B'C'D'A'所围面积相同,则两循环中,系统对外所做 净功是否相同?效率是否相同?吸收热量和放出热量是否相同?

• 4.9 两条绝热线和一条等温线能否构成一个循环过程? 为什么?
  • 4.10 判断下列叙述是否正确。
  • (1) 不可逆过程是不能实现的过程:
  • (2) 热量不能全部转化为功;
  • (3) 内能和熵是两个态函数;
• (4) 经过一个热力学过程, 若内能不变, 则熵也不变。
• 4.11 一热力学系统由初态 a 出发沿如图所示 acb 过程达到末态 b,吸收热量 330 J,对外做功 126 J。
• (1) 若它沿 adb 过程到达状态 b,对外做功 42 J, 系统吸收多少热量?
• (2) 当系统由状态 b 沿曲线 ba 返回状态 a,外界对系统做功为 84 J,此时系统是吸热还是放热? 传递的热量是多少?
• (3) 若 $E_a E_a = 170$ J, 问沿 ad 和 db 过程各吸收多少热量?

4.12 如图所示,氧气从状态 a 沿 ab 过程到达状态 b,求该过程中氧气对外做的功、内能增量和吸收的热量。

题 4.12图

4.13 一气缸内盛有 1 mol 温度为 27 ℃,压强为 1 atm 的氮气(视为刚性双原子分子理想气体),先使 其等压膨胀到原来体积的 2 倍,再等体升压使其压强 变为 2 atm,最后使其等温膨胀到压强为 1 atm。求氮气在全过程中对外做的功、内能的变化及吸收的热量。(注:1 atm=101 325 Pa,不建议使用。)

题 4.14图

• 4.14 如图所示,1 mol 的氧气,(1) 由状态 A 经历一等温过程变到状态 B; (2) 由状态 A 先经一等体过程变到状态 C, 再经一等压过程变到状态 B; (3) 由状态 A 先经一等压过程变到状态 D, 再经一等体过程变到状态 B。试分别计算以上三种情况下氧气的内能增量、所做的功及吸收的热量。

• 4. 15 质量为 $6.4 \times 10^{-2}$ kg 的氧气,温度 $t_1 = 27$ °C,体积 $V_1 = 3$ L,试计算下列两种情况下气体所做的功,并解释两种情况下做功不同的原因。
  • (1) 气体经绝热膨胀,体积变为 $V_2 = 15 L$ ;

• (2) 气体经等温膨胀,体积变为 $V_2$ = 15 L,然后再经 程。求: 等体冷却,直到温度等于绝热膨胀最后所达到的温度 (1) 为止。 (2)

• 4.16 气缸中一定量的氦气,经过绝热压缩,体积变为原来的一半,问气体分子的平均速率变为原来的几倍?

• 4.17 一定量的理想气体,其压强和体积依照 $V=ap^{-1/2}$ 的规律变化,其中 a 为已知常量。试求:

  • (1) 气体从体积 $V_1$ 膨胀到 $V_2$ 所做的功;

• (2) 体积为 $V_1$ 时的温度 $T_1$ 与体积为 $V_2$ 时的温度 $T_2$ 之比。

• 4.18 一个可以自由滑动的、不漏气的绝热活塞 把绝热容器分成两部分 I 和 II , II 中各装有物质的量为 $\nu$ 的同种刚性分子理想气体(分子的自由度为 i)。开始时,I 、II 中气体的体积相等,温度均为 I。。今用外力作用在活塞上,使其缓慢地将 I 中气体的体积压缩为原来的一半,求外力做的功。

• 4.19 1 mol 理想气体在 $T_1$ = 400 K 的高温热源与 $T_2$ = 300 K 的低温热源间做卡诺循环。已知在 400 K 的等温线上起始体积 $V_1$ = 0.001 m³,终止体积 $V_2$ = 0.005 m³,试求此气体在每一循环中;

  • (1) 从高温热源吸收的热量 $Q_{ij}$
  • (2) 气体做的净功;
  • (3) 气体传给低温热源的热量 $|Q_2|$ 。

• 4.20 一空气系统进行下述的循环:开始时压强 是1 atm,体积为22.4 L;保持体积不变,加热使压强增 加到2 atm;然后等压膨胀使体积变到33.6 L,再等体 冷却到压强为1 atm;最后经等压压缩,使气体返回到 初始状态。

  • (1) 在 p-V 图上表示出该循环过程;
  • (2) 求循环效率。
  • (注:1 atm = 101 325 Pa, 不建议使用。)

• 4.21 1 mol 氧气,经历如图所示的循环,其中 $a \rightarrow b$ 为等体过程, $b \rightarrow c$ 为等温过程, $c \rightarrow a$ 为等压过程。求:

  • (1) 净功;
  • (2) 吸收的热量;
  • (3) 循环效率。

题 4.21 图

4. 22 某种理想气体经历如图所示的循环过程, 其中 $a \rightarrow b$ 和 $c \rightarrow d$ 为绝热过程, $b \rightarrow c$ 为等体过程, $d \rightarrow a$ 为 等压过程,证明该循环的效率为 $\eta = 1 - \gamma \frac{T_d - T_a}{T_c - T_b}$ ,其中

$$\gamma = \frac{C_{p,m}}{C_{V,m}} \circ$$

题 4.22图

• 4.23 一卡诺制冷机工作时,低温热源温度为263 K,高温热源温度为284 K,在一次循环中,外界对系统做功 1000 J。此时,制冷机从低温热源吸收多少热量?
• 4.24 理想气体做卡诺循环,高温热源温度为400 K,低温热源温度为300 K,每次循环中,气体从高温热源吸收热量2500 J。求:
  • (1) 每一次循环中气体对外做的功;
  • (2) 每一次循环中向低温热源放出的热量。
• 4.25 一卡诺热机的低温热源温度为7℃,效率为40%,在保持低温热源温度不变的情况下,如果使效率提高到50%,那么高温热源的温度要提高多少?