3.6 麦克斯韦分子速率分布规律

气体分子无时无刻不在做无规则热运动。任意时刻,某个分子沿哪个方向、以多大的速率运动完全是偶然的。但是,在平衡状态下,就大量分子整体来看,它们的速率分布却遵从一定的统

文档:麦克斯韦速率分布

NOTE

3.6.1 气体分子速率分布的实验测定

计规律,这种统计规律性可通过实验来测定。

伽尔顿板实验能清楚说明这种统计规律性的存在。如图 3-5 所示,在一块竖直木板上部规则地钉有许多铁钉,木板下部设有许多等宽的竖直狭槽,板的前面覆盖上玻璃,板的顶端中部有漏斗形小口,这一装置称为伽尔顿板。实验时,将一个小球从小口投入伽尔顿板,小球在下落过程中先后与多根铁钉发生碰撞,最后落入下部的某个狭槽中。重复几次这一实验,发现小球落入哪个狭槽是不确定的,也是无法预测的。但是,如果同时在伽尔顿板中投入大量相同的小球(或将一个小球投入伽尔顿板的次数增至很大),则狭槽中小球的数目(或小球出现的次数)呈现出了一定的规律性,即中间狭槽多,两侧少。重复多次实验,小球数目(或出现次数)的这种分布几乎不变,而且,小球总数(或小球投入总次数)越大,这种分布差别越小。这说明,小球落入狭槽中的概率分布遵从一定的统计规律。

最早对气体分子速率分布的测定是法国物理学家施特恩 (0. Stem)于1920年进行的。其后,又有许多人进行了尝试,也

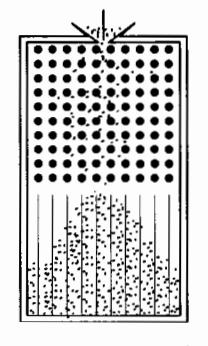
图 3-5 伽尔顿板实验

出现了许多测量方法,其中兰眉尔托的实验方法是较好的一种,其实验装置(位于真空环境中)如图 3-6 所示。将金属置于开有狭缝的容器,经加热器加热后产生金属蒸气,金属蒸气分子从容器的狭缝出射出来,并经狭缝 S 形成细分子束,射向前面的两个共轴旋转的薄金属盘,两盘间距 l,两盘上分别开有等宽的狭缝 $S_1$ 和 $S_2$ ,两狭缝错开一小角度 $\varphi$ 。当两盘以角速度 $\omega$ 转动时,分子束中仅速率满足如下关系的分子才能通过两圆盘到达探测器 P:

图 3-6 兰眉尔托的测量装置

可见,两圆盘起着速率选择器的作用。由于狭缝 $S_1$ 和 $S_2$ 都有一定宽度,因此当 $\omega$ 的大小一定时,射向探测器 P的分子的速率也并不完全相同,而是分布于一个狭窄的速率区间 $v\sim v+\Delta v$ 内。探测器 P 可探测出射向它的分子束的强度,即分子数的相对值。

改变 $\omega(\vec{y} l \pi \varphi)$ 的大小,能够通过狭缝 $S_2$ 到达探测器的分子的速率就会发生变化,因此可检测出不同速率间隔的分子束强度。将各种速率的分子数的相对值与速率进行比较,即可得出从狭缝出射出来的分子速率分布的图像。

3.6.2 麦克斯韦速率分布律

19 世纪中期,麦克斯韦利用统计力学知识从理论上推导出了气体分子速率的分布规律。在讨论麦克斯韦速率分布律之前,我们先给出速率分布函数的概念。

设一定量的理想气体处于温度为 T 的平衡状态下,分子质量为 m,总数目为 N,速率位于 $v \sim v + \Delta v$ 区间的分子数为 $\Delta N$ ,则 $\Delta N$ /N 表示速率在 $v \sim v + \Delta v$ 区间的分子数占总分子数的比率。若区间 $\Delta v$ 确定,对于不同的速率 v, 比率 $\Delta N/N$ 一般不同,即 $\Delta N/N$ 与速率 v 有关,是 v 的函数;另一方面,在给定的速率 v 附近,若区间 $\Delta v$ 不同, $\Delta N/N$ 的数值也不同,区间 $\Delta v$ 越大,分布在此区间的分子数就越多,比率 $\Delta N/N$ 的值就越大。当速率区间足够小时,用

dv 表示此小区间,在此区间的分子数为 dN,则 dN/N = f(v) dv, 或者

$$f(v) = \frac{\mathrm{d}N}{N\mathrm{d}v} \tag{3.6.2}$$

称 f(v) 为速率分布函数,它表示当分子数巨大时,分布在速率 v 附近单位速率区间的分子数占总分子数的比率。显然

$$\int_{0}^{\infty} f(v) \, \mathrm{d}v = \int_{0}^{N} \frac{\mathrm{d}N}{N} = 1$$

(3.6.3)

这称为速率分布函数 f(v) 的归一化条件。

麦克斯韦等人从理论上证明,当理想气体处于温度为T的平衡状态时,分布在 $v \sim v + dv$ 区间的分子数占总分子数的比率为

$$f(v) dv = 4\pi \left(\frac{m}{2\pi kT}\right)^{\frac{3}{2}} e^{-\frac{mv^2}{2kT}} v^2 dv$$

(3.6.4)

该式称为麦克斯韦速率分布律,其中m为分子质量,k为玻耳兹曼常量。所以麦克斯韦速率分布函数为

$$f(v) = 4\pi \left(\frac{m}{2\pi kT}\right)^{\frac{3}{2}} e^{-\frac{mv^2}{2kT}}v^2$$

(3.6.5)

此函数与速率v的关系可用曲线表示(图 3-7),称为麦克斯韦速率分布曲线。图中曲线下窄条 $v \sim v + \Delta v$ 的面积表示速率分布在此区间内的分子数 $\Delta N$ 占总分子数 N 的比率 $\Delta N/N$ 。从图中可以看出,当 $v \rightarrow 0$ 和 $v \rightarrow \infty$ 时,f(v) 的数值都很小,表明速率很小和速率很大的分子数占总分子数的比率都很小。在图示中,随着v 从v 0 逐渐增加,函数 f(v) 逐渐增大,经一极大值后又减小,与此极大值所对应的速率称为最概然速率,用 $v_p$ 表示,它的物理意义是:若将 $v \sim 0$ 的整个速率范围划分为许多相等的小区间,则气体分子分布在 $v_p$ 所在小区间的概率最大。 $v_p$ 的值可利用关系 $v \sim 0$ 确定,结果为

$$v_{p} = \sqrt{\frac{2kT}{m}} = \sqrt{\frac{2RT}{M}} \approx 1.41 \sqrt{\frac{RT}{M}}$$

(3.6.6)

将式(3.6.6)代入式(3.6.5)可得出与最概然速率 $v_p$ 所对应的曲线的峰值,其值为

$$f(v_{\rm p}) = \frac{1}{\rm e} \sqrt{\frac{8m}{\pi kT}}$$

(3.6.7)

由此可见, $f(v_p)$ 和 $v_p$ 均与分子质量 m 和温度 T 有关。图 3-8 给出了同种气体在不同温度及给定温度下不同气体分子的速率分布曲线。对于一定种类的气体(例如 $O_2$ ),温度越高,分子热运动越剧烈,所以随温度升高,气体中速率较小的分子数减少,速率较

图 3-7 气体分子速率分布

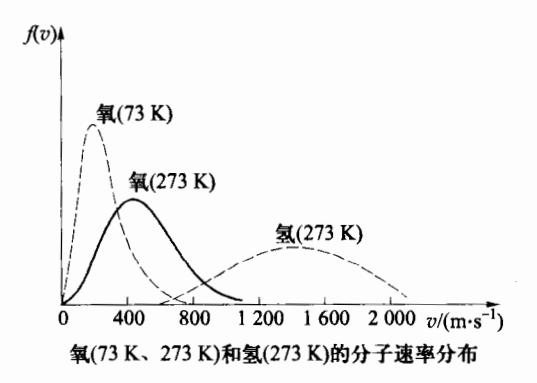
图 3-8 不同气体、不同温度的速 率分布曲线

大的分子数增加,最概然速率变大,相应的曲线峰值减小;而在给 定温度下,分子的质量越小,其最概然速率越大,曲线峰值越小。 因谏率分布函数满足归一化条件,曲线与横轴之间的总面积恒 等于1,所以当最概然速率增大、曲线峰值减低时,曲线变得 平坦。

由麦克斯韦速率分布律可求出气体分子的平均速率和方均 根速率:

(1) 平均速率 $\bar{v}$ : 气体分子速率的算术平均值。

$$$$

(2) 方均根速率 $\sqrt{v^2}$ : 气体分子速率平方平均值的平方根。 气体分子速率平方的平均值为

$$\overline{v^2} = \frac{\int_0^\infty v^2 N f(v) \, dv}{N} = \int_0^\infty v^2 f(v) \, dv = \frac{3kT}{m} = \frac{3RT}{M} \quad (3.6.9)$$

所以方均根速率为

$$\sqrt{\overline{v^2}} = \sqrt{\frac{3kT}{m}} = \sqrt{\frac{3RT}{M}} \approx 1.73 \sqrt{\frac{RT}{M}}$$

(3.6.10)

由上述结果可知,气体分子的 $v_{\scriptscriptstyle p}$ 、 $\bar{v}$ 和 $\sqrt{v^2}$ 都与 $\sqrt{T}$ 成正比.与 $\sqrt{m}$ 或 $\sqrt{M}$ 成反比。三者在量值上,有 $\sqrt{v^2} > \bar{v} > v_1$ 。这三种谏率在 不同问题中有各自的用途,在讨论分子速率分布时,用到了最概。特征速率与什么因素有关; 然速率 $v_o$ ;在计算分子平均自由程时,要用到平均速率 $\bar{v}$ ;而在计 算气体的压强、温度及分子的平均平动动能时,要用到方均根束

特征提纯与什么因素有关

计算温度为 300 K 时氧气分子的方均根速率、平均速率、最概然速率和平均平动动能。

解:方均根速率为

$$\sqrt{v^2} = \sqrt{\frac{3RT}{M}} = \sqrt{\frac{3 \times 8.314 \times 300}{32 \times 10^{-3}}} \text{ m} \cdot \text{s}^{-1}$$ $$= 4.84 \times 10^2 \text{ m} \cdot \text{s}^{-1}$$

平均速率为

$$\overline{v} = \sqrt{\frac{8RT}{\pi M}} = \sqrt{\frac{8 \times 8.314 \times 300}{3.14 \times 32 \times 10^{-3}}} \text{ m} \cdot \text{s}^{-1}$$ $$= 4.46 \times 10^{2} \text{ m} \cdot \text{s}^{-1}$$

最概然速率为

$$v_{\rm p} = \sqrt{\frac{2RT}{M}} = \sqrt{\frac{2 \times 8.314 \times 300}{32 \times 10^{-3}}} \, \text{m} \cdot \text{s}^{-1}$$

= 3.95×10² m·s^-1

平均平动动能为

$$\overline{\varepsilon}_{kt} = \frac{3}{2}kT = \frac{3}{2} \times 1.381 \times 10^{-23} \times 300 \text{ J}$$ $$= 6.21 \times 10^{-21} \text{ J}$$