2.3 刚体定轴转动的动能定理与重力场中含刚体系统的机械能守恒定律

在质点力学中,当质点受变力作用时,由牛顿第二定律导出的动能定理、功能原理与机械能守恒定律可以帮助我们解决一些牛顿定律不易解决的问题。同样,在刚体定轴转动问题中,当刚体受到变力矩作用时,由转动定律导出的有关功能关系的一些结果可以为我们解决问题提供很多帮助。

文档: 动能定理

2.3.1 力矩的功和功率

图 2-13 力矩做功

1. 力矩做功

如图 2-13 所示,设刚体可绕通过 O 点垂直图面的轴转动,作用于刚体上 P 点的力 F 使 P 点产生位移 dr,刚体转过 $d\theta$ 角度。力 F 与 P 点的位矢 r 之间的夹角为 $\varphi$ ,力 F 与位移 dr 之间的夹角为 $\alpha$ ,因 dr 很小,所以有 $\varphi+\alpha=\pi/2$ 。力 F 所做元功为

$$dW = F \cdot dr = |F| \cos \alpha |dr|$$ $$= F \cos \alpha ds = F \sin \omega r d\theta = M d\theta$$

(2. 3. 1)

式中, $|d\mathbf{r}|=d\mathbf{s}=rd\theta$ 为位移 $d\mathbf{r}$ 对应的弧长, $F\sin \varphi r=M$ 为力 F 相 对转轴 $\theta$ 的力矩大小。当刚体从角位置 $\theta$ 1 转到角位置 $\theta$ 2 时,力 $\mathbf{r}$ 6 (也即力矩 $\mathbf{r}$ 8 )所做功为

$$W = \int_{\theta_1}^{\theta_2} M d\theta \qquad (2.3.2)$$

当有多个力作用于刚体时,根据力的叠加原理,既可以先求出每个力所做功,再求代数和得到总功,也可以先求出合力矩,再积分求总功,显然二者结果是相同的。

2. 功率

功率等于单位时间所做功,根据式(2.3.1),功率可写成

$$P = \frac{\mathrm{d}W}{\mathrm{d}t} = \frac{M\,\mathrm{d}\theta}{\mathrm{d}t} = M\omega \tag{2.3.3}$$

此式表示,刚体做定轴转动时,外力矩在某时刻的功率等于该时刻的力矩与角速度的乘积。这与质点力学中的 $P=F\cdot v$ 对应。

2.3.2 刚体定轴转动的动能定理

1. 刚体定轴转动的动能

运动质点具有动能,绕固定轴转动的刚体同样具有动能。刚体转动的动能等于各个质元的动能之和,即

$$E_{k} = \sum_{i} E_{ki} = \sum_{i} \frac{1}{2} \Delta m_{i} v_{i}^{2}$$ $$= \sum_{i} \frac{1}{2} \Delta m_{i} (r_{i} \omega)^{2} = \frac{1}{2} \left( \sum_{i} \Delta m_{i} r_{i}^{2} \right) \omega^{2}$$

由于刚体的转动惯量 $I=\sum_i \Delta m_i r_i^2$ ,所以刚体转动的动能可以表示为

$$E_{k} = \frac{1}{2}I\omega^{2} \tag{2.3.4}$$

此式表明: 刚体定轴转动的动能等于刚体对转轴的转动惯量与角速度平方的乘积的 1/2。这与质点动能的表达式 $E_k = mv^2/2$ 是对应的。

2. 刚体定轴转动的动能定理

由刚体定轴转动定律式(2.2.4),有 $M = I\beta = I \frac{d\omega}{dt}$ ,将其代人式(2.3.2)中,得

$$W = \int_{\theta_1}^{\theta_2} M \, \mathrm{d}\theta = \int_{\theta_1}^{\theta_2} I \, \frac{\mathrm{d}\omega}{\mathrm{d}t} \, \mathrm{d}\theta = \int_{\omega_1}^{\omega_2} I \omega \, \mathrm{d}\omega$$

式中, $\omega_1$ 对应刚体在角位置 $\theta_1$ 处的角速度大小, $\omega_2$ 对应刚体在角位置 $\theta_2$ 处的角速度大小;并且用到 $\omega = d\theta/dt$ 。积分上式,注意到刚体相对定轴的转动惯量 I 为定值,以及刚体转动的动能表达式(2.3.4),结果为

$$W = \int_{\theta_1}^{\theta_2} M d\theta = \frac{1}{2} I \omega_2^2 - \frac{1}{2} I \omega_1^2 = \Delta E_k$$

(2.3.5)

此式表明:在刚体做定轴转动时,合外力矩对刚体所做的功等于 刚体转动动能的增量。这一结论称为刚体定轴转动的动能定理。

这与质点的动能定理

$$W = \int_a^b \mathbf{F} \cdot d\mathbf{r} = \frac{1}{2} m v_2^2 - \frac{1}{2} m v_1^2 = \Delta E_k$$

对应。

值得注意的是,在质点力学中,讨论质点系的动能定理时,结论是所有外力和内力对质点系所做的功等于质点系动能的增量。 之所以含有内力的功,是因为质点系中各个质点之间的相对位置是可以改变的,虽然每对内力大小相等方向相反,但每对内力所做的功不一定被抵消。因此质点系动能定理中含有内力所做功一项。对于刚体来说,各个质元之间虽有内力作用,但各个质元之间的距离保持不变,每对内力所做功相互抵消,整个刚体所有内力做功之和为零。因此在刚体转动动能定理式(2.3.5)中只有外力的功而没有内力的功。

例题 2-9

利用刚体定轴转动的动能定理,重新求解例题 2-7 中均匀 细棒下摆通过竖直位置时的角速度大小(图 2-14)。

解:转轴对细棒的作用力通过轴线,其力矩为零。因此,细棒下摆过程中只有重力矩作用。细棒在任意 $\theta$ 角位置时所受重力矩大小为 M=mg $\frac{l}{2}\cos\theta$ ,从 $\theta=0$ 到 $\theta=\frac{\pi}{2}$ ,重力

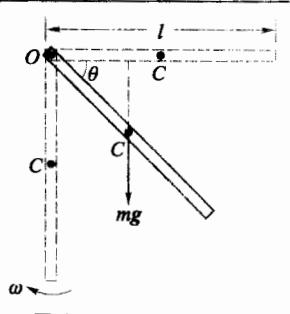
图 2-14 细棒的转动

矩做功为

$$W = \int_0^{\pi/2} mg \, \frac{l}{2} \cos \theta \, d\theta = \frac{mgl}{2}$$

初态细棒静止,转动动能 E, = 0;末态细棒

处于竖直位置,转动动能 $E_{k2} = \frac{1}{2}I\omega^2$ 。由刚

体定轴转动的动能定理,有

$$W = \Delta E_{k} = \frac{1}{2}I\omega^{2} - 0$$

将积分所得 W 的值及细棒转动惯量 $I=ml^2/3$ 代人,解出 $\omega=\sqrt{3g/l}$ 。

2.3.3

重力场中含刚体系统的机械 施守恒定律

1. 刚体的重力势能

刚体中所有质元相对地球的重力势能之和,就是刚体的重力势能。刚体的重力势能应理解为刚体与地球所组成的物体系所 共有。

选取地面附近某一高度作为重力势能零点,以此为原点 O、竖直向上作为 z 坐标轴正方向。设刚体中某一质量为 $\Delta m_i$ 的质元其坐标为 $z_i$ ,此质元的重力势能为 $E_{pi} = \Delta m_i g z_i$ ,对刚体中所有质元的重力势能求和,即得到整个刚体的重力势能。刚体的质量是连续分布的,求和可用积分表示,于是有

$$E_{p} = \sum_{i} \Delta m_{i} g z_{i} = g \sum_{i} \Delta m_{i} z_{i}, \quad E_{p} = g \int z dm$$

根据质心定义式(1.6.4), $z_c = \frac{1}{m} \int z dm$ ,代入上式,得刚体的重力势能表达式为

$$E_n = mgz_C \tag{2.3.6}$$

上式表明, 刚体的重力势能等于刚体所受的重力与刚体质心相对 零势能点的高度的乘积。也可以理解为, 刚体的重力势能与一个 刚体全部质量集中于质心处的质点的重力势能相等。

2. 重力场中含刚体系统的机械能守恒

重力矩做功本质上仍是重力做功,重力是保守力,因此,当只有重力作用时,含有刚体的物体系统的机械能守恒。

下面,通过两个具体的例子加以说明。

利用重力场中含刚体系统的机械能守恒关系,再次求解例题2-7中均匀细棒下摆通过 竖直位置时的角速度大小(图 2-14)。

解:转轴对细棒的作用力通过轴线,其力矩为零。因此,细棒下摆过程中只有重力矩作用,将细棒与地球作为系统,则系统机械能守恒。选取细棒下摆至竖直位置时质心 C(即细棒的中点)的高度为重力势能的零点。初态细棒水平静止,转动动能 $E_{k1}=0$ ,重力势能 $E_{p1}=mgl/2$ ;末态细棒处于竖直位置,转动动能 $E_{k2}=l\omega^2/2$ ,重力势能 $E_{p2}=0$ 。

初、末态机械能相等,即

$$E_{k1} + E_{p1} = E_{k2} + E_{p2}$$

上述各量代入,得

$$0+mg\frac{l}{2}=\frac{1}{2}I\omega^2+0$$

将细棒转动惯量 $I = ml^2/3$ 代人,解出 $\omega = \sqrt{3g/l}$ 。

例题 2-11

如图 2-15 所示,细绳的上端缠绕在质量为 $m_1$ 、半径为 R 的定滑轮上,细绳的下端与质量为 $m_2$ 的物体相连,系统初态静止。此后物体下落并带动定滑轮转动,求物体下落 h 高度时的速率 v。不计一切阻力,细绳不可伸长且质量可以忽略,定滑轮相对转轴 O 的转动惯量为 $I=m_1R^2/2$ 。

解:可用两种方法求解。

解法一:利用质点的动能定理及刚体定 轴转动的动能定理

以物体 $m_2$ 为研究对象,作用于物体 $m_2$ 上的是两个恒力,一个是竖直向下的重力,大小为 $m_2g$ ;另一个是竖直向上的绳子张力,大小为 $F_T$ 。物体初态静止,动能为零;当其下落 h 高度后,动能变为 $m_2v^2/2$ 。根据质点的动能定理,合外力所做的功等于物体动能的增量,有

$$(m_2g-F_T)h=\frac{1}{2}m_2v^2-0$$

再以定滑轮 m₁ 为研究对象,物体 m₂ 下落 h 高度的过程中,定滑轮转过的角度为

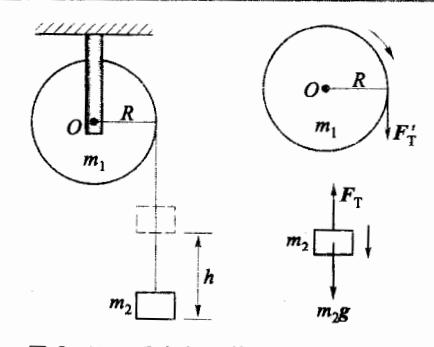
图 2-15 质点与刚体的运动

$\Delta\theta = h/R$ 。定滑轮所受绳子张力是恒力,大小为 $F_{1}'$ ,相对转轴 $O, F_{1}'$ 的力矩大小为 $F_{1}'R$ 。定滑轮初态静止,转动动能为零;转过 $\Delta\theta$ 角度后,转动动能变为 $I\omega^{2}/2$ 。根据 刚体定轴转动的动能定理,合外力矩所做的功等于刚体转动动能的增量,有

$$F_{\rm T}'R\Delta\theta = \frac{1}{2}I\omega^2 - 0$$

按线量与角量的关系,物体的速率v与定滑轮角速度的大小 $\omega$ 满足

$$v = R\omega$$

绳中张力 $F_T$ 和 $F_T'$ 是一对作用力和反作用

力,大小相等方向相反。上面列方程时,已 经考虑了两者的方向,方程中的 $F_{T}$ 和 $F_{T}'$ 只 是数值大小,两者应相等,即 $F_{T}'=F_{T}$ 。联立上述各式,并将定滑轮的转动惯量代人,解得

$$v = 2\sqrt{\frac{m_2gh}{m_1 + 2m_2}}$$

解法二:利用重力场中含刚体系统的机 械能守恒关系

将物体、定滑轮、绳及地球组成系统 (物体系)。系统外力不做功;绳中张力为 内力,对定滑轮做正功 $F_T'R\Delta\theta = F_Th$ ,对物体

做负功- $F_rh$ ,两者的代数和为零;只有重力这个保守力做功不为零,系统机械能守恒。选取物体下落末态高度为重力势能零点,系统初态静止,只有物体的重力势能 $m_2gh$ ;末态物体动能为 $m_2v^2/2$ ,定滑轮转动动能为 $I\omega^2/2$ ,则有

$$m_2gh = \frac{1}{2}m_2v^2 + \frac{1}{2}I\omega^2$$

将定滑轮的转动惯量和 $v=R\omega$ 代人,即可解出 v,结果同上。

此外,本题还可用牛顿第二定律及刚体 转动定律求解,从略。