8.2 麦克斯韦方程组

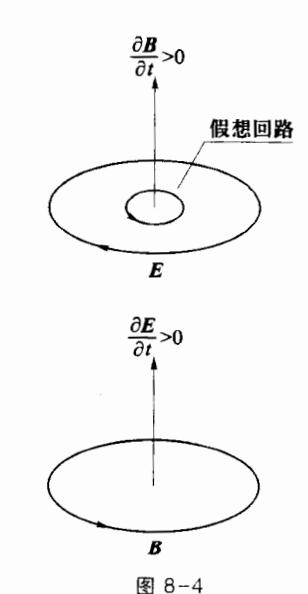
麦克斯韦引入了位移电流和位移电流密度后,使全电流线成为了永远的闭合曲线,揭示了除了传导电流产生磁场外,变化的电场也能产生磁场,可用图 8-4 将变化的电场产生的磁场与变化的磁场产生的电场加以对比。

麦克斯韦在系统地研究了各种电磁现象后,提出了变化的磁场可以产生涡旋的感应电场的理论,从而合理地解释了法拉第电磁感应定律;引入了位移电流的假设,这不仅保持了电流的连续性,而且推广了安培环路定理。1853年,麦克斯韦将描述电磁现象的全部规律归纳在一个方程组中,此即人们所称的麦克斯韦方程组。

根据麦克斯韦理论,在一般情况下,电场 E 和电位移场 D 是由净电荷激发的 $E^{(1)}$ 、 $D^{(1)}$ 和变化磁场激发的 $E^{(2)}$ 、 $D^{(2)}$ 共同组成,即

$$E = E^{(1)} + E^{(2)}$$

$D = D^{(1)} + D^{(2)}$

因此,E 的环流为

$$\oint_{I} \boldsymbol{E} \cdot d\boldsymbol{l} = \oint_{I} (\boldsymbol{E}^{(1)} + \boldsymbol{E}^{(2)}) \cdot d\boldsymbol{l} = \oint_{I} \boldsymbol{E}^{(1)} \cdot d\boldsymbol{l} + \oint_{I} \boldsymbol{E}^{(2)} \cdot d\boldsymbol{l}$$

由于静电场中的环路积分为零,即 $\oint_l E^{(1)} \cdot dl = 0$ ,感应电场的环路积分为

$$\oint_{l} E^{(2)} \cdot dl = -\int_{S} \frac{\partial B}{\partial t} \cdot dS$$

代入上式后得

$$\oint_{l} \mathbf{E} \cdot d\mathbf{l} = -\int_{s} \frac{\partial \mathbf{B}}{\partial t} \cdot d\mathbf{S}$$

(8.2.1)

上式即为法拉第电磁感应定律,其物理意义为:在任意电场 E中的环路积分,等于该环路所围面积内磁通量随时间变化率的 负值。

而电位移 D 的通量为

$$\oint_{S} \mathbf{D} \cdot d\mathbf{S} = \oint_{S} (\mathbf{D}^{(1)} + \mathbf{D}^{(2)}) \cdot d\mathbf{S} = \oint_{S} \mathbf{D}^{(1)} \cdot d\mathbf{S} + \oint_{S} \mathbf{D}^{(2)} \cdot d\mathbf{S}$$

其中静电场中电位移通量由高斯定理得出

$$\oint_{S} \mathbf{D}^{(1)} \cdot d\mathbf{S} = q = \int_{V} \rho \, dV$$

而由于感应电场 $E^{(2)}$ 和感应电位移场 $D^{(2)}$ 均为涡旋场, $E^{(2)}$ 和

We can scarcely avoid the inference that light consists in the transverse undulations of the same medium which is the cause of electric and magnetic phenomena. (James Clerk Maxwell)

NOTE

$D^{(2)}$ 线是都闭合曲线,所以 $D^{(2)}$ 穿过任意闭合曲面的通量等于零,即

$$\oint_{S} \boldsymbol{D}^{(2)} \cdot d\boldsymbol{S} = 0$$

因此有

$$\oint_{c} \mathbf{D} \cdot d\mathbf{S} = \int_{V} \rho \, dV \tag{8.2.2}$$

此式为电场中的高斯定理,反映出电场的性质。

同样,在一般情况下,H 和 B 也是由传导电流和位移电流共同产生的。设由传导电流产生的磁场强度、磁感应强度分别为 $H^{(1)}$ 、 $B^{(1)}$ ;由位移电流产生的磁场强度、磁感应强度分别为 $H^{(2)}$ 、 $B^{(2)}$ 。由于无论何种原因产生的 B 线都是闭合曲线,所以通过任何闭合曲面磁感应强度 B 的通量恒为零,即

$$\oint_{S} \mathbf{B} \cdot d\mathbf{S} = 0 \tag{8.2.3}$$

此式称为磁场中的高斯定理,反映出任何情况下 B 场都是涡旋场,描述磁场的曲线都是闭合的,单一磁荷是不存在的。

而磁场强度 H 的环流为

$$\oint_{l} \boldsymbol{H} \cdot d\boldsymbol{l} = \oint_{l} (\boldsymbol{H}^{(1)} + \boldsymbol{H}^{(2)}) \cdot d\boldsymbol{l} = \oint_{l} \boldsymbol{H}^{(1)} \cdot d\boldsymbol{l} + \oint_{l} \boldsymbol{H}^{(2)} \cdot d\boldsymbol{l}$$

由安培环路定理, $\oint_{l} \boldsymbol{H}^{(1)} \cdot d\boldsymbol{l} = I_{c} = \int_{s} \boldsymbol{J}_{c} \cdot d\boldsymbol{S}$ 。式中 $I_{c}$ 代表传导电

流, $J_c$ 代表传导电流密度。又由 $\oint_t \boldsymbol{H}^{(2)} \cdot d\boldsymbol{l} = \int_s \frac{\partial \boldsymbol{D}}{\partial t} \cdot d\boldsymbol{S}$ ,将两式同时代入上式得

$$\oint_{l} \boldsymbol{H} \cdot d\boldsymbol{l} = \int_{s} \left( \boldsymbol{J}_{c} + \frac{\partial \boldsymbol{D}}{\partial t} \right) \cdot d\boldsymbol{S}$$

(8.2.4)

式(8.2.4)称为全电流安培环路定理,反映出产生磁场的两种原因,即传导电流和变化的电场。

应该指出,对于静电场和恒定磁场而言,电场 E、电位移 D、磁感应强度 B 和磁场强度 H 都只是位置的函数,而与时间无关;而麦克斯韦引入了位移电流和涡旋电场后,E、D、B、H 不仅仅是位置的函数,而且还是时间的函数。

将式(8.2.1)、(8.2.2)、(8.2.3)、(8.2.4)写在一起,称为麦克斯韦方程组:

麦克斯韦方程组中的各方程分别 具有什么意义?

$$\oint_{l} \mathbf{E} \cdot d\mathbf{l} = -\int_{s} \frac{\partial \mathbf{B}}{\partial t} \cdot d\mathbf{S}$$ $$\oint_{s} \mathbf{D} \cdot d\mathbf{S} = \int_{V} \rho dV\hfill (8.2.5)$$ $$\oint_{s} \mathbf{B} \cdot d\mathbf{S} = 0$$ $$\oint_{l} \boldsymbol{H} \cdot d\boldsymbol{l} = \int_{S} \left( \boldsymbol{J}_{c} + \frac{\partial \boldsymbol{D}}{\partial t} \right) \cdot d\boldsymbol{S}$$

在此, 笔者认为有必要着重强调其中的第一式和第四式的物 理意义。第一式:着重强调了变化的磁场会产生涡旋电场;第四 式:着重强调传导电流和变化的电场都能激发磁场,结合其中的 第三式,说明不论是什么原因形成的磁场都是涡旋场,描述磁场 的场线都是闭合曲线。

如果考虑到有电磁场存在的空间中充满各项各向同性介质 的情况,上述麦克斯韦方程组还不算完备,须考虑各种场量还有 如下关系:

$$D = \varepsilon E$$ $$B = \mu H$$ $$J = \sigma E$$

麦克斯韦方程组在电磁学中的地位十分重要,相当于力学中 的牛顿定律。原则上讲,只要知道了各种场量的边界条件和初始 条件,一切有关电磁场中的动力学问题都能够描述。麦克斯韦方 程组不仅是电磁学的理论基础,而且也是波动光学的理论基础, 有关这一点在以后的电磁波和波动光学等章节中会显现出来。

▲ 文档:电磁震荡和电磁波