8.1 位移电流

如图 8-1 所示的恒定电流条件下,传导电流 $I_c$ 与它所建立的磁场间满足安培环路定理,即

$$\oint_{I} \boldsymbol{H} \cdot d\boldsymbol{I} = I_{c} = \int_{S} \boldsymbol{J}_{c} \cdot d\boldsymbol{S}$$

(8.1.1)

无论回路是位于真空还是位于有磁介质存在的空间,上式都是成立的。上式中的l为积分环路, $I_c$ 则是穿过以l为边界的任意曲面S上的传导电流, $J_c$ 为传导电流密度。以l为边界可以围出任意多个形状不同的曲面。图8-1中的 $S_1$ 和 $S_2$ 共同构成闭合曲面 $S(S=S_1+S_2)$ 。通过 $S_1$ 面的电流为流入闭合面S的电流,通过 $S_2$ 面的电流为流出闭合面S的电流。对于恒定电流来说,流入与流出闭合面S的传导电流相等。恰好满足恒定电流的连续性方程:

$$\oint_{S} \boldsymbol{J}_{c} \cdot d\boldsymbol{S} = 0 \tag{8.1.2}$$

但是,对于回路中电流是随时间变化的非恒定电流来说,式(8.1.1)和式(8.1.2)两式将不再成立。

以电容器的充放电为例,如图 8-2 所示,在电容器充放电的过程中,仍然应用安培环路定理(8.1.1),并将积分环路 l 取在靠近电容器的一个极板处,以 l 为边界分别围出 $S_1$ 和 $S_2$ 两个曲面,曲面 $S_1$ 与导线相交,曲面 $S_2$ 位于两极板之间,对于曲面 $S_1$ ,式 (8.1.1)依然成立,即

$$\oint_{I} \boldsymbol{H} \cdot d\boldsymbol{I} = \int_{S_{c}} \boldsymbol{J}_{c} \cdot d\boldsymbol{S} = I_{c}$$

(8.1.3)

式(8.1.3)说明充电过程中导线中的电流传入了曲面 $S_1$ ,而对曲面 $S_2$ 来说,由于没有导线穿过,两极板间也没有可以自由移动的电荷,因此,也就没有传导电流通过 $S_2$ 面。对 $S_2$ 面,有

$$\oint_{l} \boldsymbol{H} \cdot d\boldsymbol{l} = \int_{S_{2}} \boldsymbol{J}_{c} \cdot d\boldsymbol{S} = 0$$

(8.1.4)

(8.1.3)、(8.1.4)两式的结果不同,即安培环路定理对于通过相同的环路 l 围出的不同曲面有不同的结果,说明在非恒定电流条件下,安培环路定理式(8.1.1)和电流连续性方程式(8.1.2)都不再成立。为了解决这一矛盾,必须对式(8.1.1)和式(8.1.2)两式加以修正,使它们对非恒定电流也能成立。

通过对电容器充放电过程的观察,发现传导电流在电容器极板上中断的同时,极板上聚集了电荷 q,q 分布在电容器内表面上。 $q=S_A\sigma,S_A$ 为极板面积, $\sigma$ 为电荷面密度。q 的存在使电容器在两极板间建立起电位移场,即 D 场。由静电学中的高斯定理可以得到

$$D = \sigma$$

, $\Psi = S_A D = S_A \sigma$

当电容器充电时,导线上的传导电流逐渐减小,与此同时,极板上的电荷 q 和电荷面密度 $\sigma$ ,以及极板间的电位移 D 的大小、电位移通量 $\Psi$ 的数值却在增大。当电容器放电时,导线上传导电流逐渐减小,极板上的 q 和 $\sigma$ 及极板间的 D 和 $\Psi$ 的数值也随之减小。即在导线上的传导电流变化时,极板上的 q 和 $\sigma$ 及极板间的 D 和 $\Psi$ 都随之而变,其规律为

$$\frac{\mathrm{d}\Psi}{\mathrm{d}t} = \frac{\mathrm{d}(S_{\mathrm{A}}D)}{\mathrm{d}t} = \frac{\mathrm{d}(S_{\mathrm{A}}\sigma)}{\mathrm{d}t} = \frac{\mathrm{d}q}{\mathrm{d}t} = I_{c}$$

(8.1.5)

如果仍选图 8-2 中的闭合曲面 S,则上式中的 I。就是通过导线流入曲面 S,的电流,即

$$I_{c} = -\oint_{S} \boldsymbol{J}_{c} \cdot d\boldsymbol{S} = -\int_{S_{c}} \boldsymbol{J}_{c} \cdot d\boldsymbol{S}$$

(8.1.6)

$n\frac{d\Psi}{dt}$ 则是通过两极板间的曲面 $S_2$ 流出去的"电流",即

$$\frac{\mathrm{d}\boldsymbol{\Psi}}{\mathrm{d}t} = \frac{\mathrm{d}}{\mathrm{d}t} \oint_{S} \boldsymbol{D} \cdot \mathrm{d}\boldsymbol{S} = \frac{\mathrm{d}}{\mathrm{d}t} \int_{S_{2}} \boldsymbol{D} \cdot \mathrm{d}\boldsymbol{S}$$

(8.1.7)

两式在数值上相等,即

$$-\int_{S_1} \boldsymbol{J}_c \cdot d\mathbf{S} = \frac{\mathrm{d}}{\mathrm{d}t} \int_{S_2} \boldsymbol{D} \cdot d\mathbf{S} = \int_{S_2} \frac{\partial \boldsymbol{D}}{\partial t} \cdot d\mathbf{S} \qquad (8.1.8)$$

然而就其实质来说, $\frac{\mathrm{d}\Psi}{\mathrm{d}t}$ 并非真正意义上的电流,它不是由电

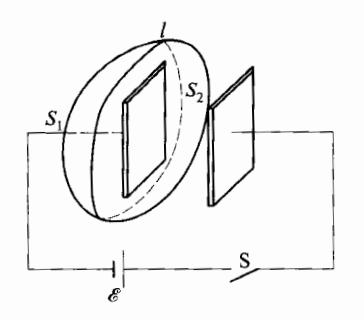
图 8-2 电容器充电

位移电流的实质是什么?

荷定向移动形成的电流,麦克斯韦将 $\frac{\mathrm{d} \boldsymbol{\Psi}}{\mathrm{d} t}$ 定义为位移电流,用 $I_a$ 表示;将 $\frac{\partial \boldsymbol{D}}{\partial t}$ 定义为位移电流密度,用 $J_a$ 表示,即

$$I_{\rm d} = \frac{\mathrm{d}\Psi}{\mathrm{d}t} \tag{8.1.9}$$ $$\boldsymbol{J}_{\mathrm{d}} = \frac{\partial \boldsymbol{D}}{\partial t} \tag{8.1.10}$$

位移电流也有流向,通过观察发现,在电容器充电时,极板上的 q 要增加,极板间的 D 就要增大,此时 $\frac{\partial D}{\partial t}$ 的方向与 D 一致,也与导线上的传导电流方向一致,如图 8-3(a) 所示,在电容器放电时,极板上 q 减小,两极板间 D 的数值减小,此时 $\frac{\partial D}{\partial t}$ 与 D 反向,但仍与导线上传导电流有相同的流向。因此可以看出,不论电容器是充电还是放电,传导电流都与位移电流有相同的流向。

在引入了位移电流 $I_a$ 和位移电流密度 $J_a$ 后,就可以对安培定理式(8.1.1)及电流的连续性方程式(8.1.2)进行修正。

由式(8.1.6)和式(8.1.7)相等,得

$$-\oint_{S} \boldsymbol{J}_{c} \cdot d\boldsymbol{S} = \frac{d}{dt} \oint_{S} \boldsymbol{D} \cdot d\boldsymbol{S} = \oint_{S} \frac{\partial \boldsymbol{D}}{\partial t} \cdot d\boldsymbol{S}$$

整理后得到

$$\oint_{S} \left( \boldsymbol{J}_{c} + \frac{\partial \boldsymbol{D}}{\partial t} \right) \cdot d\boldsymbol{S} = 0$$

令 $J_{\pm} = J_{c} + \frac{\partial D}{\partial t}, J_{\pm}$ 称为全电流密度,则上式为

$$\oint_{\mathcal{S}} \mathbf{J}_{\hat{\Xi}} \cdot d\mathbf{S} = 0 \tag{8.1.11}$$

这就是全电流的连续性方程,该方程对恒定电流与非恒定电流都适用。

同样,将传导电流 $I_c$ 与位移电流 $I_d$ 之和定义为全电流,即 $I_{\alpha} = I_c + I_d$ 。于是安培环路定理可写为

$$\oint_{I} \boldsymbol{H} \cdot d\boldsymbol{l} = I_{\hat{x}} = I_{c} + I_{d} = I_{c} + \frac{d\Psi}{dt}$$

(8.1.12)

对于恒定电流的情况,电位移矢量的大小不随时间变化, $\frac{\partial \mathbf{D}}{\partial t} = 0$ ,则 $\frac{\mathrm{d} \boldsymbol{\Psi}}{\mathrm{d} t} = 0$ ,将此结果代人式(8.1.11)、式(8.1.12)后,其结果又与式(8.1.1)、式(8.1.2)一致了。

图 8-3 传导电流与位移电流的 关系