7.4.1 动生电动势
当导体在磁场中运动而切割磁感应线时,导体中将产生电动势 E \mathcal{E} E
如图 7-4 所示,在一个磁感应强度为 B,方向垂直纸面向内的均匀恒定磁场中,有一根长度为 l 的金属导体杆 ab,平行纸面放置。当它以图示的速度 v 由左向右均速运动时,杆中所有的自由电子都同时具有了速度 v,因此每个电子所受的洛伦兹力 F m = ( − e ) v × B F_m = (-e)v \times B F m = ( − e ) v × B
F m − e = v × B \frac{\boldsymbol{F}_{\scriptscriptstyle m}}{-e} = \boldsymbol{v} \times \boldsymbol{B} − e F m = v × B 这个力正是产生电源电动势的非静电力,相应的"非静电场场强"为 E k = F m − 1 = v × B E_{\mathbf{k}} = \frac{F_{\mathbf{m}}}{-1} = \mathbf{v} \times \mathbf{B} E k = − 1 F m = v × B
E i = ∫ − + E k ⋅ d l = ∫ a b ( F m − e ) ⋅ d l = ∫ a b ( v × B ) ⋅ d l \mathcal{E}_{i} = \int_{-}^{+} \boldsymbol{E}_{k} \cdot d\boldsymbol{l} = \int_{a}^{b} \left( \frac{\boldsymbol{F}_{m}}{-e} \right) \cdot d\boldsymbol{l} = \int_{a}^{b} (\boldsymbol{v} \times \boldsymbol{B}) \cdot d\boldsymbol{l} E i = ∫ − + E k ⋅ d l = ∫ a b ( − e F m ) ⋅ d l = ∫ a b ( v × B ) ⋅ d l E i = ∫ a b ( v × B ) ⋅ d l ( 7.4.1 ) \mathcal{E}_{i} = \int_{a}^{b} (\boldsymbol{v} \times \boldsymbol{B}) \cdot d\boldsymbol{l} \qquad (7.4.1) E i = ∫ a b ( v × B ) ⋅ d l ( 7.4.1 ) 即
由于上述例子中 v ⊥ B v \perp B v ⊥ B v × B v \times B v × B
E i = ∫ 0 b v B d l = v B l \mathscr{E}_{i} = \int_{0}^{b} vB dl = vBl E i = ∫ 0 b v B d l = v Bl 如果在磁场保持不变的情况下,在磁场中再放置一个如图 7-5 所示金属导体框架 edcf,金属杆 ab 位于 x 处,并与框一起围出闭合回路 abcda,回路所围面积 S=lx,穿过该面积的磁通量为 Φ = S B = l x B \Phi=SB=lxB Φ = SB = l x B v = d x d t v=\frac{\mathrm{d}x}{\mathrm{d}t} v = d t d x Φ \Phi Φ
E i = − d Φ d t = − B l d x d t = − B l v \mathcal{E}_{i} = -\frac{\mathrm{d}\boldsymbol{\Phi}}{\mathrm{d}t} = -Bl\,\frac{\mathrm{d}\boldsymbol{x}}{\mathrm{d}t} = -Bl\boldsymbol{v} E i = − d t d Φ = − Bl d t d x = − Bl v
文档:动牛与感牛电动势
图 7-4 动生电动势中的洛伦兹力
图 7-5 闭合回路中的动生电动势
其大小和方向都与金属杆 ab 单独做同样移动时所得结果一样, 只不过由于杆和框构成了一闭合导体回路,才有电流在回路中 通过。
以上结果说明,即使在闭合导体回路中,也只是导体回路中运动的部分才产生动生电动势,或者说动生电动势只能存在于导体回路中运动的部分上,而导体回路中不动的部分只相当于与电源相连接的外电路,只为电荷的定向移动提供了一条通道。上式中的 l 所代表的恰好是导体回路中参与运动的部分。
从式(7.4.1)还可以看出,并非金属杆在磁场中所作的任何运动都能产生动生电动势,例如导体杆沿着 B 的方向运动。不会产生动生电动势。只有 v × B ≠ 0 v \times B \neq 0 v × B = 0 v × B v \times B v × B
如果将一根任意形状的导线放在一非均匀磁场中,并且导线各部分运动的速度各不相同,此种情况下,要求出整根导线所生动生电动势,应首先在导线中任选一段线元 dI,dI 的方向可沿导线人为设定,则该段导线所生动生电动势为
d E i = ( v × B ) ⋅ d l (7.4.2) d\mathcal{E}_i = (\mathbf{v} \times \mathbf{B}) \cdot d\mathbf{l} \tag{7.4.2} d E i = ( v × B ) ⋅ d l ( 7.4.2 ) 式中,v为某个瞬时 dl的速度,B 为 dl 所在处的磁感应强度。
对上式积分得出整根导线产生的动生电动势(7.4.1)。若所求的 E > 0 \mathcal{E}_{>0} E > 0 E < 0 \mathcal{E}_{<0} E < 0
例题 7-1
如图 7-6 所示,在磁感应强度为 B 的均匀磁场中,有一长为 L 的金属杆 OA 垂直于磁场,并绕杆的 O 端以匀角速度 ω \omega ω
解:由于杆做转动,所以杆上各处的线速度都不相同,因此有必要在杆的任意位置处取一线元 dl。设 dl 的方向由 O 到 A,位置距 O 点为 l,利用式 (7.4.2) 并考虑到 v ⊥ B v \perp B v ⊥ B ∣ v × B ∣ = v B |v \times B| = vB ∣ v × B ∣ = v B v = l ω v = l\omega v = l ω
E i = ∫ d E i = ∫ ( v × B ) ⋅ d l = − ∫ 0 L l ω B d l \mathscr{E}_{i} = \int d\mathscr{E}_{i} = \int (\boldsymbol{v} \times \boldsymbol{B}) \cdot d\boldsymbol{l} = -\int_{0}^{L} l\omega B dl E i = ∫ d E i = ∫ ( v × B ) ⋅ d l = − ∫ 0 L l ω B d l
= − 1 2 L 2 ω B =-\frac{1}{2}L^2\omega B = − 2 1 L 2 ω B 式中负号表示 E i \mathcal{E}_i E i d I \mathrm{d} I d I
7.4.2 感生电动势
除了动生电动势外,实验还表明,即使导体回路与磁场不存在相对运动,但是只要穿过回路所围面积的磁通量发生变化,回路中仍然能产生电动势。按照法拉第电磁感应定律,这个电动势 E i = − d Φ d t = − ∫ s ∂ B ∂ t ⋅ d S \mathcal{E}_i = -\frac{\mathrm{d}\boldsymbol{\Phi}}{\mathrm{d}t} = -\int_s \frac{\partial \boldsymbol{B}}{\partial t} \cdot \mathrm{d}\boldsymbol{S} E i = − d t d Φ = − ∫ s ∂ t ∂ B ⋅ d S
那么产生感生电动势的非静电力是什么呢? 麦克斯韦在认真研究的基础上,给出了答案,他指出:在变化的磁场周围存在着感应电场 E i E_i E i
感应电场 E i E_i E i E i E_i E i E i E_i E i
以上分析可知,感生电动势中的非静电力源于感应电场。根据电动势的定义,在一个闭合导体回路 l 中感生电动势为
∮ l E i ⋅ d l = − ∫ S ∂ B ∂ t ⋅ d S \oint_{l} \boldsymbol{E}_{i} \cdot d\boldsymbol{l} = -\int_{S} \frac{\partial \boldsymbol{B}}{\partial t} \cdot d\boldsymbol{S} ∮ l E i ⋅ d l = − ∫ S ∂ t ∂ B ⋅ d S (7.4.3)
式中,积分区域S是积分回路l所包围的面积。
利用矢量分析中的斯托克斯公式,得
∫ S ( ∇ × E i ) ⋅ d S = − ∫ S ∂ B ∂ t ⋅ d S \int_{S} (\nabla \times \boldsymbol{E}_{i}) \cdot d\boldsymbol{S} = -\int_{S} \frac{\partial \boldsymbol{B}}{\partial t} \cdot d\boldsymbol{S} ∫ S ( ∇ × E i ) ⋅ d S = − ∫ S ∂ t ∂ B ⋅ d S ∇ × E i = − ∂ B ∂ t \nabla \times \boldsymbol{E}_{i} = -\frac{\partial \boldsymbol{B}}{\partial t} ∇ × E i = − ∂ t ∂ B (7.4.4)
此式为电磁感应定律的微分形式,其物理意义为:如果某个区域存在着磁感应强度的变化,则在其周围就会激发一个涡旋的感应电场 E i E_i E i ∂ B ∂ t \frac{\partial B}{\partial t} ∂ t ∂ B E i E_i E i
为什么感应电场不能用电势指出。
图 7-7 感应电场
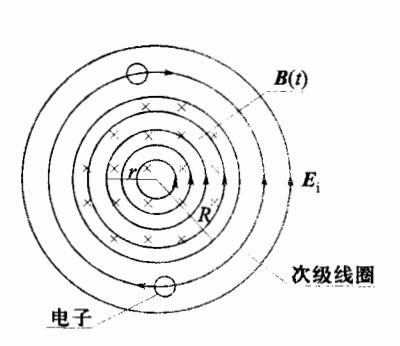
所有微小涡旋场矢量叠加后的形状。例如对于一个长直螺线管, 在其横截面上感应电场线的形状就是以螺线管的轴线为心的同 心圆环,并且感应电场遍及管的内外。
例题 7-2
在一半径为R的圆柱形空间内,充满一均匀磁场,磁感应强度B沿柱的轴线,在柱形空间的某一截面上,如图 7-8 所示,放置一长为L的金属棒 ab,求:(1)当B以速率 d B d t \frac{dB}{dt} d t d B E \mathcal{E} E
解:(1)由于对称性可以判断,在所选择的截面上,感应电场 E i E_i E i Φ \Phi Φ E i \mathcal{E}_i E i E i E_i E i ∮ L E i ⋅ d l = − ∫ S ∂ B ∂ t ⋅ d S \oint_{L} E_i \cdot dl = -\int_{S} \frac{\partial B}{\partial t} \cdot dS ∮ L E i ⋅ d l = − ∫ S ∂ t ∂ B ⋅ d S E i E_i E i E i E_i E i π r \pi r π r
当 r < R 时,式(7.4.3)右边的积分结果为 − ∫ s ∂ B ∂ t ⋅ d S = ∂ B ∂ t π r 2 -\int_s \frac{\partial \boldsymbol{B}}{\partial t} \cdot d\boldsymbol{S} = \frac{\partial \boldsymbol{B}}{\partial t} \pi r^2 − ∫ s ∂ t ∂ B ⋅ d S = ∂ t ∂ B π r 2 d S d\boldsymbol{S} d S ∂ B ∂ t \frac{\partial \boldsymbol{B}}{\partial t} ∂ t ∂ B
E i = r 2 ∂ B ∂ t ( r < R ) E_{i} = \frac{r}{2} \frac{\partial B}{\partial t} \quad (r < R) E i = 2 r ∂ t ∂ B ( r < R ) 当积分回路位于柱体之外(r>R)时,由于磁感应场完全集中在柱体之内,所以式(7.4.3)右边积分结果为
− ∫ S ∂ B ∂ t ⋅ d S = ∂ B ∂ t π R 2 -\int_{S} \frac{\partial \mathbf{B}}{\partial t} \cdot d\mathbf{S} = \frac{\partial \mathbf{B}}{\partial t} \pi R^{2} − ∫ S ∂ t ∂ B ⋅ d S = ∂ t ∂ B π R 2
图 7-8 例题 7-2 图
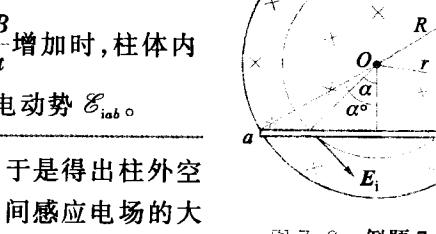
E i = R 2 2 r ∂ B ∂ t ( r > R ) E_{i} = \frac{R^{2}}{2r} \frac{\partial B}{\partial t} \quad (r > R) E i = 2 r R 2 ∂ t ∂ B ( r > R ) (2) 由分析得知,使杆 ab 产生感应电动势 E i , a b \mathcal{E}_{i,ab} E i , ab E i E_i E i E i E_i E i
E i a b = ∫ a b E i ⋅ d l = ∫ a b E i cos α d l \mathscr{E}_{iab} = \int_{a}^{b} \mathbf{E}_{i} \cdot d\mathbf{l} = \int_{a}^{b} \mathbf{E}_{i} \cos \alpha d\mathbf{l} E iab = ∫ a b E i ⋅ d l = ∫ a b E i cos α d l 考虑到
小为
E i = r 2 ∂ B ∂ t , r = R 2 − ( L / 2 ) 2 cos α , E_i = \frac{r}{2} \frac{\partial B}{\partial t}, \quad r = \frac{\sqrt{R^2 - (L/2)^2}}{\cos \alpha}, E i = 2 r ∂ t ∂ B , r = cos α R 2 − ( L /2 ) 2 , cos α d l = r d α \cos \alpha dl = r d\alpha cos α d l = r d α
所以有
E i a b = ∫ − α 0 α R 2 − ( L / 2 ) 2 2 cos 2 α ( ∂ B ∂ t ) d α \mathscr{E}_{iab} = \int_{-\alpha_0}^{\alpha} \frac{R^2 - (L/2)^2}{2\cos^2 \alpha} \left(\frac{\partial B}{\partial t}\right) d\alpha E iab = ∫ − α 0 α 2 cos 2 α R 2 − ( L /2 ) 2 ( ∂ t ∂ B ) d α 解出以上积分,并考虑到 tan α=
L / 2 R 2 − ( L / 2 ) 2 \frac{L/2}{\sqrt{R^2-(L/2)^2}} R 2 − ( L /2 ) 2 L /2 ,所以得
E i a b = L 2 R 2 − ( L / 2 ) 2 ( ∂ B ∂ t ) \mathcal{E}_{iab} = \frac{L}{2} \sqrt{R^2 - (L/2)^2} \left( \frac{\partial B}{\partial t} \right) E iab = 2 L R 2 − ( L /2 ) 2 ( ∂ t ∂ B )