メインコンテンツまでスキップ

7.3 法拉第电磁感应定律

法拉第在反复实验的基础上,通过认真分析研究,意识到导体回路中之所以出现感应电流,其原因是导体回路中存在着感应电动势 E\mathcal{E} ,并且提出如下电磁感应定律。

当穿过导体回路所包围面积中的磁通量 Φ\Phi 随时间变化时,回路中即产生感应电动势 Ei\mathcal{E}_i , Ei\mathcal{E}_i 的大小与 Φ\Phi 对时间的变化率 dΦdt\frac{\mathrm{d}\Phi}{\mathrm{d}t} 成正比,加上脚标 i 的电动势特指由感应而生成的电动势,即

Ei=−KdΦdt\mathscr{E}_{i} = -K \frac{\mathrm{d} \Phi}{\mathrm{d} t}

式中 K 为比例系数,当 Φ\Phi 的单位用 Wb( 韦伯),时间用 s( 秒),电 动势的单位用 V( 伏特)时,K=1,于是有

文档:法拉第电磁感应定律

The five essential entreprecional skills for success an embeddiscrimination, occasization, inactivation, and communication. Whither bandleys

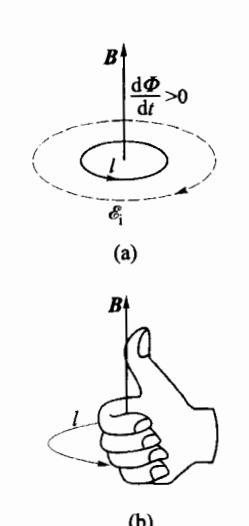
图 7-3 电磁感应定律

法拉第电磁感应定律中回路的方 向和面积的方向是怎么规定的?

Ei=−dΦdt(7.3.1)\mathscr{E}_{i} = -\frac{\mathrm{d}\boldsymbol{\Phi}}{\mathrm{d}t} \tag{7.3.1}

式中负号表示感应电动势的方向与磁通量变化的关系。

由式(7.3.1)确定 Ei\mathcal{E}_i 的方向,可以采用右手螺旋定则。先使右手拇指指向 B\mathbf{B} 的方向,然后弯曲的四指指尖的方向设定为回路 l 的方向。当穿过回路 l 所围面积上的磁通量 Φ\mathbf{\Phi} 随时间增大时,即 dΦdt>0\frac{d\mathbf{\Phi}}{dt}>0 ,根据式(7.3.1),必然有 Ei=−dΦdt<0\mathcal{E}_i=-\frac{d\mathbf{\Phi}}{dt}<0 ,所以 Ei\mathcal{E}_i 的方向应与所设定 l 的方向相反,如图 7-3 所示;反之,若磁通量 Φ\mathbf{\Phi} 随时间减小,即 dΦdt<0\frac{d\mathbf{\Phi}}{dt}<0 ,则必然有 Ei=−dΦdt>0\mathcal{E}_i=-\frac{d\mathbf{\Phi}}{dt}>0 ,此时 Ei\mathcal{E}_i 的方向与所设环路 l 的方向相同。

如果导体回路是由 N 匝线圈绕制而成,则穿过回路所包围面积的总磁通量,应该是穿过各匝线圈所包围面积磁通量的和,即 Ψ=∑iNΦi\Psi = \sum_{i}^{N} \Phi_{i} 。 Ψ\Psi 是总磁通量,常称为磁链。整个导体回路的总感应电动势,是磁链对时间变化率的负值,即

Ei=−dΨdt(7.3.2)\mathscr{E}_{i} = -\frac{\mathrm{d}\Psi}{\mathrm{d}t} \tag{7.3.2}

上式也相当于各匝线圈所产生的感应电动势之和,即

Ei=Ei1+Ei2+⋯+EiN=−ddt(Φ1+Φ2+⋯+ΦN)\mathcal{E}_{i} = \mathcal{E}_{i1} + \mathcal{E}_{i2} + \dots + \mathcal{E}_{iN} = -\frac{d}{dt} (\boldsymbol{\Phi}_{1} + \boldsymbol{\Phi}_{2} + \dots + \boldsymbol{\Phi}_{N})

若通过以上各匝线圈所围面积的磁通量 Φ 都相等,则

Ψ=∑iNΦi=NΦ(7.3.3)\Psi = \sum_{i}^{N} \Phi_{i} = N\Phi \tag{7.3.3}

总感应电动势为

Ei=−dΨdt=−NdΦdt(7.3.4)\mathscr{E}_{i} = -\frac{\mathrm{d}\Psi}{\mathrm{d}t} = -N\frac{\mathrm{d}\Phi}{\mathrm{d}t} \tag{7.3.4}

当导体回路中的总电阻为 R 时,回路中的感应电流为

Ii=EiR=−NRdΦdtI_{i} = \frac{\mathcal{E}_{i}}{R} = -\frac{N}{R} \frac{\mathrm{d}\boldsymbol{\Phi}}{\mathrm{d}t}

(7.3.5)

由于 Φ=∫SB⋅dS\Phi = \int_{S} \mathbf{B} \cdot d\mathbf{S} ,所以有

Ei=−dΦdt=−ddt∫SB⋅dS\mathcal{E}_i = -\frac{\mathrm{d}\boldsymbol{\Phi}}{\mathrm{d}t} = -\frac{\mathrm{d}}{\mathrm{d}t} \int_{S} \boldsymbol{B} \cdot \mathrm{d}\boldsymbol{S}

该式的积分遍及导体回路所包围的全部曲面 S。若 S 不随时间变化,上式可表示为

Ei=−∫S∂B∂t⋅dS\mathscr{E}_{i} = -\int_{S} \frac{\partial \mathbf{B}}{\partial t} \cdot d\mathbf{S}

(7.3.6)