文档:电流与磁场 高斯
某些物体具有吸引铁、钴、镍及其合金的特性,这种性质称为磁性,具有磁性的物体称为磁体。大约在公元前 600 多年,人们就注意到某些铁矿石(例如 F e 3 O 4 Fe_3O_4 F e 3 O 4
6.2.1 磁场和磁感应强度
实验发现,运动电荷之间除了有库仑力作用外,还存在着相互作用的磁力。研究认为,这种磁力是通过磁场传递的,而这个磁场恰恰是运动电荷建立的。描述磁场的物理量称为磁感应强度,用 B 表示。
磁感应强度 B 是矢量。研究 B 在空间的分布可以采用多种方法。而利用通有电流为 I 的微型平面线圈来探测磁感应强度 B 的空间分布就是其中一种。
如图 6-5 所示,设微型平面线圈所围面积为 Δ S \Delta S Δ S
图 6-5 磁感应强度
的作用相当于一个小磁针。用磁矩 m 来表示其大小和方向, m = I Δ S e n m = I\Delta Se_n m = I Δ S e n Δ S \Delta S Δ S
将该线圈置入磁场某位置稳定后,微型载流线圈磁矩 m 的方向即为该点处 B 的方向。而偏离这个方向时,线圈都将受到一个力矩 M 的作用,使 m 趋向于 B。当 m 与 B 相垂直时,m 所受力矩达到最大值 M m a x M_{max} M ma x M m a x M_{max} M ma x
B = M max m (6.2.1) B = \frac{M_{\text{max}}}{m} \tag{6.2.1} B = m M max ( 6.2.1 ) 在国际单位制中, 磁感应强度 B 的单位是 T (特斯拉, 简称特) ( 1 T = 1 N ⋅ A − 1 ⋅ m − 1 ) (1 T=1 N \cdot A^{-1} \cdot m^{-1}) ( 1 T = 1 N ⋅ A − 1 ⋅ m − 1 ) ( c m ⋅ g ⋅ s ) (cm \cdot g \cdot s) ( c m ⋅ g ⋅ s ) 1 T = 10 4 G s 1 T=10^4 Gs 1 T = 1 0 4 G s
6.2.2 毕奥-萨伐尔定律
毕奥-萨伐尔定律(简称毕-萨定律)是研究电流产生磁场的 重要规律。利用毕-萨定律结合场强的叠加原理,原则上可以求 出任意形状的载流导线在空间产生的磁感应强度 B 。
如图 6-6 所示,一段通有电流 I 的弯曲导线,在它周围建立了磁场。为了求出空间任意点 P 处的磁感应强度 B,可以设想将导线划分成许多小段 dI,每一小段 IdI 称为电流元。电流元为一矢量,其方向为 dI 所在处电流流动的方向。毕一萨定律给出任意电流元 IdI 在 P 点处产生的磁感应强度为
d B = μ 0 4 π I d l × e r r 2 d\mathbf{B} = \frac{\mu_0}{4\pi} \frac{Id\mathbf{l} \times \mathbf{e}_r}{r^2} d B = 4 π μ 0 r 2 I d l × e r (6.2.2)
式中,e,表示沿径矢 r 的单位矢量; μ 0 \mu_0 μ 0 μ 0 = 4 π \mu_0 = 4\pi μ 0 = 4 π 10 − 7 10^{-7} 1 0 − 7 -2 。dB 方向垂直于电流元 IdI 和径向单位矢量 e,构成的平面,与 IdI、e,满足右手螺旋关系。
磁场与电场一样,遵从场强叠加原理,所以每个电流元 IdI 在 P 点处产生的磁感应强度 dB 的矢量和即为整段载流线在 P 点处产生的磁感应强度,即
B = ∫ d B = μ 0 4 π ∫ I d l × e r r 2 \boldsymbol{B} = \int \mathrm{d}\boldsymbol{B} = \frac{\mu_0}{4\pi} \int \frac{\mathrm{Id}\boldsymbol{l} \times \boldsymbol{e}_r}{r^2} B = ∫ d B = 4 π μ 0 ∫ r 2 Id l × e r 在实际应用中,首先应该建立合适的坐标系,将载流线中任
图 6-6 毕-萨定律
意电流元 Idl 在场点处产生的磁感应强度 dB 向各坐标轴上投影,使之变成标量,然后再分别对 dB 在各坐标轴上的分量求和,即积分,积分遍布所讨论的整段载流线。
例题 6-1
求长为L、通有电流I的长直导线在空间产生的磁感应强度B。
解:如图 6-7,建立直角坐标系,以竖直导线为y轴,y轴与电流方向相同,以过场点P且与y轴相垂直的直线为x轴。在距原点为y处取电流元 Idy。应用毕-萨定律得该电流元在P点产生的磁感应强度的大小为
d B = μ 0 4 π I d y sin θ r 2 dB = \frac{\mu_0}{4\pi} \frac{Idy \sin \theta}{r^2} d B = 4 π μ 0 r 2 I d y sin θ (1)
由于载流直导线上任一电流元在 P 点产生的 dB 都具有相同的方向,即垂直纸面向内,故长为 L 的导线在 P 点所产生的磁感应强度 B 的大小,可以通过对上式的积分求得,积分遍布该载流长直导线:
B = ∫ L d B = μ 0 4 π ∫ L I d y sin θ r 2 B = \int_{L} dB = \frac{\mu_0}{4\pi} \int_{L} \frac{I dy \sin \theta}{r^2} B = ∫ L d B = 4 π μ 0 ∫ L r 2 I d y sin θ (2)
为了计算该积分,应将上式中的变量 d y ⋅ θ dy \cdot \theta d y ⋅ θ
取 θ \theta θ α \alpha α θ \theta θ π \pi π
sin α = sin θ \sin \alpha = \sin \theta sin α = sin θ , r = x sin α = x sin θ r = \frac{x}{\sin \alpha} = \frac{x}{\sin \theta} r = s i n α x = s i n θ x γ = x cot α = − x cot θ \gamma = x \cot \alpha = -x \cot \theta γ = x cot α = − x cot θ
图 6-7 例题 6-1图
取 y 的微分 dy =
x d θ sin 2 θ \frac{x d\theta}{\sin^2 \theta} sin 2 θ x d θ 代人式(2),得
B = μ 0 4 π ∫ θ 1 θ 2 I sin θ d θ x = μ 0 I 4 π x ( cos θ 1 − cos θ 2 ) B = \frac{\mu_0}{4\pi} \int_{\theta_1}^{\theta_2} \frac{I \sin \theta d\theta}{x} = \frac{\mu_0 I}{4\pi x} (\cos \theta_1 - \cos \theta_2) B = 4 π μ 0 ∫ θ 1 θ 2 x I sin θ d θ = 4 π x μ 0 I ( cos θ 1 − cos θ 2 ) (6. 2. 3)
式中, θ 1 \theta_1 θ 1 θ 2 \theta_2 θ 2 θ \theta θ
当导线长度 L ≫ x L\gg x L ≫ x θ 1 = 0 \theta_1=0 θ 1 = 0 θ 2 = π \theta_2=\pi θ 2 = π
B = μ 0 I 2 π x B = \frac{\mu_0 I}{2\pi x} B = 2 π x μ 0 I (6.2.4)
例题 6-2
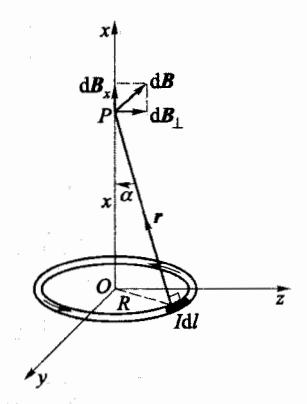
求通有电流 I,半径为 R 的载流圆环形导线在其对称轴上某点处的磁感应强度 B。
解:建立如图 6-8 所示的空间直角坐标系,载流圆环位于 yz 的平面之内,且圆心与坐标原点重合,场点 P 位于 z 轴上 z 点
处。然后于载流圆环任意位置处取电流元 IdI,该电流元在 P 点产生的磁感应强度为
图 6-8 例题 6-2图
d B = μ 0 4 π I d l × e r r 2 d\boldsymbol{B} = \frac{\mu_0}{4\pi} \frac{Id\boldsymbol{l} \times \boldsymbol{e}_r}{r^2} d B = 4 π μ 0 r 2 I d l × e r 载流圆环上的每个电流元 Idl 都与其到场点 P 的矢量 r 垂直,即 Idl 与 e,的夹角处处为 θ = π / 2 \theta=\pi/2 θ = π /2
产生磁感应强度 B 的值,可以对 dB 进行积分,但是过程比较复杂。简单的方法是将 dB 分解为沿 x 轴方向的分量 d B x dB_x d B x d B x dB_x d B x d B x dB_x d B x
B = ∫ d B x = ∫ d B sin α = μ 0 4 π ∫ I d l r 2 R r B = \int dB_x = \int dB \sin \alpha = \frac{\mu_0}{4\pi} \int \frac{Idl}{r^2} \frac{R}{r} B = ∫ d B x = ∫ d B sin α = 4 π μ 0 ∫ r 2 I d l r R 当P点选定后,r即为定值,不随电流元 IdI 选取位置而变,所以
B = μ 0 I R 4 π r 3 ∫ 0 2 π R d l = μ 0 R 2 I 2 ( R 2 + x 2 ) 3 / 2 B = \frac{\mu_0 IR}{4\pi r^3} \int_0^{2\pi R} dl = \frac{\mu_0 R^2 I}{2 (R^2 + x^2)^{3/2}} B = 4 π r 3 μ 0 I R ∫ 0 2 π R d l = 2 ( R 2 + x 2 ) 3/2 μ 0 R 2 I (6.2.5)
式中, r = R 2 + x 2 r = \sqrt{R^2 + x^2} r = R 2 + x 2 B 0 = μ 0 I 2 R i B_0 = \frac{\mu_0 I}{2R}i B 0 = 2 R μ 0 I i
例题 6-3
如图 6-9 所示,有一段半径为 R,孤度为 Φ \Phi Φ
解:如图 6-9 所示,在该圆弧导线的任意位置取电流元 IdI,电流元在场点 O 处的磁感应强度为 B,用右手螺旋定则可以判断其方向为垂直纸面向外,故有
d B = μ 0 4 π I d l × e r r 2 d\boldsymbol{B} = \frac{\mu_0}{4\pi} \frac{Id\boldsymbol{l} \times \boldsymbol{e}_r}{r^2} d B = 4 π μ 0 r 2 I d l × e r 由于圆弧导线各处的电流元 Idl 总是与其到场点的径矢 r 相垂直,即两矢量间的夹角处处为 π / 2 \pi/2 π /2
d B = μ 0 I 4 π d l R 2 = μ 0 I 4 π R d φ R 2 = μ 0 I 4 π d φ R dB = \frac{\mu_0 I}{4\pi} \frac{dl}{R^2} = \frac{\mu_0 I}{4\pi} \frac{R d\varphi}{R^2} = \frac{\mu_0 I}{4\pi} \frac{d\varphi}{R} d B = 4 π μ 0 I R 2 d l = 4 π μ 0 I R 2 R d φ = 4 π μ 0 I R d φ 对整段载流弧形导线积分,得出
B = ∫ 0 ϕ μ 0 I 4 π d φ R = μ 0 I 4 π R Φ ( 6.2.6 ) B = \int_0^{\phi} \frac{\mu_0 I}{4\pi} \frac{d\varphi}{R} = \frac{\mu_0 I}{4\pi R} \Phi \quad (6.2.6) B = ∫ 0 ϕ 4 π μ 0 I R d φ = 4 π R μ 0 I Φ ( 6.2.6 )
图 6-9 例题 6-3 图
此结果适用于任意弧度角的载流圆弧形导线在其曲率中心处产生的磁感应强度 B,只要将其所对应的弧度 Φ \Phi Φ 2 π 2\pi 2 π
B = μ 0 I 4 π R Φ Φ = 2 π = μ 0 I 2 π 4 π R = μ 0 I 2 R B = \frac{\mu_0 I}{4\pi R} \Phi_{\Phi = 2\pi} = \frac{\mu_0 I 2\pi}{4\pi R} = \frac{\mu_0 I}{2R} B = 4 π R μ 0 I Φ Φ = 2 π = 4 π R μ 0 I 2 π = 2 R μ 0 I 例题 6-4
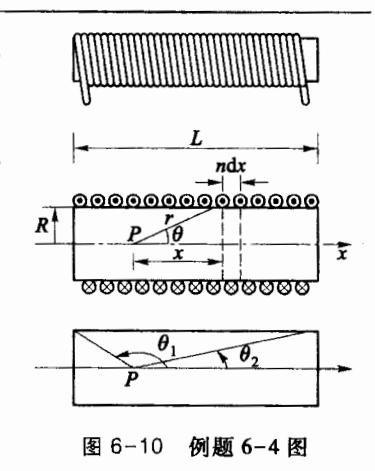
求长直载流螺线管在其轴线上任意点处的磁感应强度。已知螺线管长为L,截面半径为R,单位长度上线圈的匝数为n,通过电流为I,如图 6-10 所示。
解:长直螺线管是由导线在圆柱表面密绕而成的螺线形线圈。当导线很细、缠绕很密时,可以把它看成是一系列半径相同、载有相同电流、同轴紧密排列的线圈。
选螺线管的轴线向右为 x 轴的正方向, 选场点 P 与坐标原点重合,在距 P 点为 x 处 选长度为 dx 的一小段螺线管。 dx 所对应 的载流线圈的匝数为 ndx,每一匝通有电流 I 的线圈在 P 点处产生的磁感应强度,可以 通过式(6.2.4)计算,而 ndx 匝线圈在 P 处 的磁感应强度可由下式计算:
d B = μ 0 R 2 I 2 ( R 2 + x 2 ) 3 / 2 n d x i d\mathbf{B} = \frac{\mu_0 R^2 I}{2(R^2 + x^2)^{3/2}} n dx i d B = 2 ( R 2 + x 2 ) 3/2 μ 0 R 2 I n d x i 由图可知: x = R cot θ x = R\cot \theta x = R cot θ d x = − R csc 2 θ d θ dx = -R \csc^2 \theta d\theta d x = − R csc 2 θ d θ R 2 + x 2 = R 2 csc 2 θ R^2 + x^2 = R^2 \csc^2 \theta R 2 + x 2 = R 2 csc 2 θ
d B = μ 0 ln ln 2 ( − sin θ d θ ) \mathrm{d}B = \frac{\mu_0 \ln \ln}{2} (-\sin \theta \mathrm{d}\theta) d B = 2 μ 0 ln ln ( − sin θ d θ ) 从螺线管左端向右端积分,对应的角度从 θ 1 \theta_1 θ 1 θ 2 \theta_2 θ 2
B = μ 0 I n 2 ∫ θ 1 θ 2 ( − sin θ d θ ) = μ 0 I n 2 ( cos θ 2 − cos θ 1 ) B = \frac{\mu_0 In}{2} \int_{\theta_1}^{\theta_2} (-\sin \theta d\theta) = \frac{\mu_0 In}{2} (\cos \theta_2 - \cos \theta_1) B = 2 μ 0 I n ∫ θ 1 θ 2 ( − sin θ d θ ) = 2 μ 0 I n ( cos θ 2 − cos θ 1 ) 如果这个螺线管的长度 L 远远大于其截面的半径 R ( L ≫ R ) R(L\gg R) R ( L ≫ R ) θ 2 ≈ 0 \theta_2\approx 0 θ 2 ≈ 0
θ 1 ≈ π \theta_1 \approx \pi θ 1 ≈ π
B = μ 0 n I B = \mu_0 nI B = μ 0 n I 对螺线管右端 θ 2 = π / 2 \theta_2 = \pi/2 θ 2 = π /2 θ 1 = π \theta_1 = \pi θ 1 = π θ 2 = 0 \theta_2 = 0 θ 2 = 0 θ 1 = π / 2 \theta_1 = \pi/2 θ 1 = π /2
B = μ 0 n I 2 B = \frac{\mu_0 nI}{2} B = 2 μ 0 n I 图 6-11 反映了载流螺线管轴线上的磁感应场的分布。实验证明,只要是螺线的长度 L 远大于其横截面的半径,都可以将其视为"无限长"螺线管,对于"无限长"螺线管内部,除了在两端附近外,其他区域均为一均匀磁场。
图 6-11 长直螺线管轴线上的磁场分布
6.2.3 运动电荷的磁场
电流是电荷定向运动产生的,电流产生磁场的实质是运动电荷产生磁场。通过对毕-萨定律的讨论。可以得出运动电荷产生
的磁场。
由毕-萨定律可以得出一个运动电荷在空间产生的磁场,由毕-萨定律可知任意电流元 IdI 在空间某点处产生的磁感应强度为 d B = μ 0 4 π I d I × e r r 2 dB = \frac{\mu_0}{4\pi} \frac{IdI \times e_r}{r^2} d B = 4 π μ 0 r 2 I d I × e r B q B_q B q I = d Q d t = v d S n q I = \frac{dQ}{dt} = vdSnq I = d t d Q = v d S n q
d B = μ 0 4 π ( v d S n q ) d l × e r r 2 = μ 0 4 π ( n d S d l ) q v × e r r 2 d\mathbf{B} = \frac{\mu_0}{4\pi} \frac{(vdSnq) dl \times \mathbf{e}_r}{r^2} = \frac{\mu_0}{4\pi} \frac{(ndSdl) q\mathbf{v} \times \mathbf{e}_r}{r^2} d B = 4 π μ 0 r 2 ( v d S n q ) d l × e r = 4 π μ 0 r 2 ( n d S d l ) q v × e r 式中由于电荷的运动方向与电流元 IdI 的方向一致,故以 v 承担电流元的方向。小柱体内的电荷数 dN = ndSdI,故单个运动电荷在 P 点产生的磁感应强度为
B q = d B d N = μ 0 4 π q v × e r r 2 \boldsymbol{B}_{q} = \frac{\mathrm{d}\boldsymbol{B}}{\mathrm{d}N} = \frac{\mu_{0}}{4\pi} \frac{q\boldsymbol{v} \times \boldsymbol{e}_{r}}{r^{2}} B q = d N d B = 4 π μ 0 r 2 q v × e r (6.2.7)
当 q 为正电荷时,B 的方向就是 v × e v \times e v × e v × e v \times e v × e
图 6-12 运动电荷的磁场