一
→ 文档:电容 电场能量
前面讨论了静电场中的导体和电介质,由它们适当组合就可以得到一种在实际应用中有重要价值的电器元件——电容器。
5.7.1 孤立导体的电容
所谓孤立导体,是指导体周围既没有其他导体存在也没有电介质存在的情况。设想有一球形的导体,并设它带电荷量为Q,该导体便具有了一定的电势V。当所带电荷量增加时,导体的电势V也随之增加。但是,电荷量与电势V的比值 Q V \frac{Q}{V} V Q
C = Q V (5.7.1) C = \frac{Q}{V} \tag{5.7.1} C = V Q ( 5.7.1 ) 在国际单位制中,电容的单位是 F(法拉),1 F=1 C/1 V。由于这个单位太大,实际中常用 μ F \mu F μ F μ F = 10 − 6 \mu F=10^{-6} μ F = 1 0 − 6 p F = 10 − 12 pF=10^{-12} pF = 1 0 − 12
C = Q V = Q Q / ( 4 π ε 0 R ) = 4 π ε 0 R C = \frac{Q}{V} = \frac{Q}{Q/(4\pi\varepsilon_0 R)} = 4\pi\varepsilon_0 R C = V Q = Q / ( 4 π ε 0 R ) Q = 4 π ε 0 R 按上式推算,一个1F电容的孤立导体球,其半径将约为地球半径的1400倍。若将地球视为孤立导体球,利用上式估算,地球的电容仅为7×10-4 F,可见F这个单位实在太大。
实际上,孤立导体是不存在的,任何导体周围都存在着其他
NOTE
物体(导体或电介质)。这些物质的存在都将对原本"孤立"导体的电势产生影响,从而影响它的容电能力。为了避免外界的影响,可以利用静电屏蔽的方法。
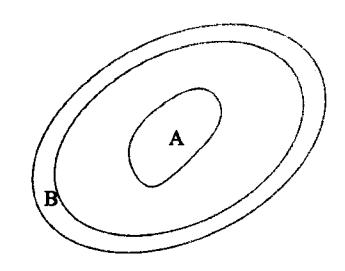
如图 5-49 所示,将导体 A 放置在一个导体空腔 B 之内,构成一个导体系,称这种导体系为电容器。而 A 和 B 分别代表电容器的两个极。当 A 极带有电荷 Q 时,B 极的内表面上会感应出等量异号电荷-Q。当 A 极上电荷增加时,B 极上的异号电荷就会等量增加;两极间的电场 E 及两极间的电势差 U A B U_{AB} U A B U A B U_{AB} U A B
C = Q U A R (5.7.2) C = \frac{Q}{U_{AR}} \tag{5.7.2} C = U A R Q ( 5.7.2 ) 式中,C即为电容器的电容值,其单位与孤立导体的电容单位一样,为F(法拉)。
实际上,作为电容器,对导体系屏蔽状态的要求并不十分严格,只要从一个极上发出电场线的大多数都汇聚在另一个极板上就可以了。例如,一对平行导体板,只要它们相对面积的线度远大于它们之间的距离,它们的电场线就几乎全集中在两板之间,这对平行导体板就可以视为理想电容器。
电容器的应用十分广泛,首先电容器可以产生适合人们需要的各种电场。例如,用一对平行板电容器可以产生一个均匀电场;其次,电容器可以在一个狭小的空间(即两极间)储存能量。另外,电容器和其他器件的组合,可以发生脉冲信号,发出或探测电磁振荡。总之,电容器是电子时代不可或缺的电子器件。
5.7.2 几种典型电容器的计算
电容器的电容定义式(5.7.2),对于计算各种形状电容器的电容都是适用的。具体做法是:假设电容器的某一极上所带电荷量为 Q,然后计算两极间的电势差。对于多数情形,电势差可由式(5.3.8)来计算,这就需要首先知道两极间的场强分布。所以,电容计算仍是一个场强计算问题。下面举几种典型实例。
1. 平行板电容器
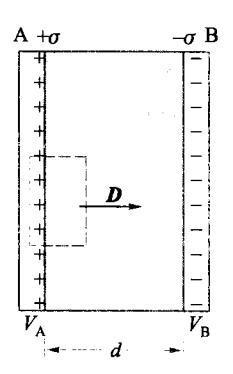
这是一种最常见的电容器。如图 5-50 所示,其构造是大小相同平行放置的两块平行导体板。在导体板之间充满相对介电常量为 ε \varepsilon ε d ≪ S d \ll \sqrt{S} d ≪ S
图 5-49 静电屏蔽
图 5-50 平行板电容器
为计算它的电容,任意设定极板 A、B 各带电荷量为 Q、-Q,忽略边缘效应,电荷均匀分布在两导体板相对的内表面,其电荷面密度分别为 σ \sigma σ − σ -\sigma − σ D = σ D=\sigma D = σ D = ε E D=\varepsilon E D = εE
E = D ε = σ ε r ε 0 E = \frac{D}{\varepsilon} = \frac{\sigma}{\varepsilon_r \varepsilon_0} E = ε D = ε r ε 0 σ 依式(5.3.8)得出两极板间的电势差,即
U A B = ∫ A B E ⋅ d l = σ d ε r ε 0 U_{AB} = \int_{A}^{B} \mathbf{E} \cdot d\mathbf{l} = \frac{\sigma d}{\varepsilon_{r} \varepsilon_{0}} U A B = ∫ A B E ⋅ d l = ε r ε 0 σ d 依式(5.7.2)得
C = Q U A B = ε 0 ε r S d C = \frac{Q}{U_{AB}} = \frac{\varepsilon_0 \varepsilon_r S}{d} C = U A B Q = d ε 0 ε r S (5.7.3)
从上式可以看出,平行板电容器的电容与导体板的面积成正 比,与电介质的相对介电常量成正比,而与两极板间距离成反比。 为了提高平行板电容器的电容,应设法使极板的面积加大;精选 相对介电常量较高而又耐压的电介质;同时尽量减小两极板间的 距离。基于此,人们制造了一种实用的电容器,这种电容器是两 片又薄又窄又长的金属箔作为电极,在金属箔之间加上一层电介 质纸,然后将它们卷起来,就构成了纸介电容器。这仅仅是各种 各样实用电容器的一种。
2. 球形电容器
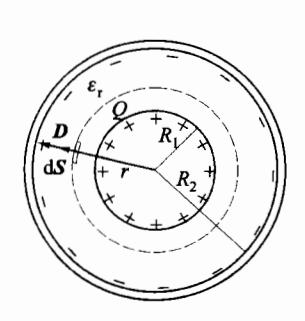
图 5-51 为两个同心导体球壳,其内球壳的半径为 R 1 R_1 R 1 R 2 R_2 R 2 ϵ \epsilon ϵ
假设内球壳带电荷量 Q,外球壳内表面感应出电荷量 -Q,于两球之间作半径为 r 的同心球形高斯面。利用电介质中的高斯定理式(5.6.7)得
D = Q 4 π r 2 e r D = \frac{Q}{4\pi r^2} e_r D = 4 π r 2 Q e r 由 D = ε E D = \varepsilon E D = εE
E = Q 4 π ε 0 ε r r 2 e r E = \frac{Q}{4\pi\varepsilon_0\varepsilon_r r^2}e_r E = 4 π ε 0 ε r r 2 Q e r 由式(5.3.8)求得两球壳间电势差为
U 12 = ∫ R 1 R 2 E ⋅ d l = Q ( R 2 − R 1 ) 4 π ε 0 ε 1 R 1 R 2 U_{12} = \int_{R_1}^{R_2} \mathbf{E} \cdot d\mathbf{l} = \frac{Q(R_2 - R_1)}{4\pi\varepsilon_0\varepsilon_1 R_1 R_2} U 12 = ∫ R 1 R 2 E ⋅ d l = 4 π ε 0 ε 1 R 1 R 2 Q ( R 2 − R 1 ) 依式(5.7.2)得
图 5-51 球形电容器
C = Q U 12 = 4 π ε 0 ε r R 1 R 2 R 2 − R 1 C = \frac{Q}{U_{12}} = \frac{4\pi\varepsilon_0\varepsilon_r R_1 R_2}{R_2 - R_1} C = U 12 Q = R 2 − R 1 4 π ε 0 ε r R 1 R 2 (5.7.4)
当 R 2 R_2 R 2 R 1 R_1 R 1 R 2 → R 1 R_2 \rightarrow R_1 R 2 → R 1
C = Q U 12 = 4 π ε 0 ε r R 2 R 2 − R 1 = ε 0 ε r S d C = \frac{Q}{U_{12}} = \frac{4\pi\varepsilon_0\varepsilon_r R^2}{R_2 - R_1} = \frac{\varepsilon_0\varepsilon_r S}{d} C = U 12 Q = R 2 − R 1 4 π ε 0 ε r R 2 = d ε 0 ε r S 式中, d = R 2 − R 1 d=R_2-R_1 d = R 2 − R 1 R 2 ≫ R 1 R_2\gg R_1 R 2 ≫ R 1 R 2 → ∞ R_2\to\infty R 2 → ∞ C = 4 π ε 0 ε r R 1 C=4\pi\varepsilon_0\varepsilon_rR_1 C = 4 π ε 0 ε r R 1
3. 柱形电容器
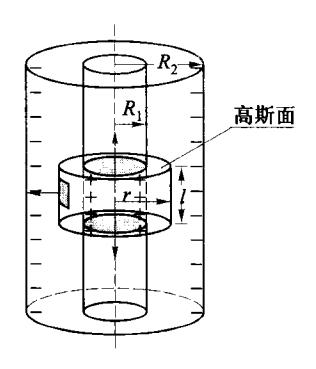
如图 5-52 所示,一个半径为 R 1 R_1 R 1 R 2 R_2 R 2 ε \varepsilon ε λ \lambda λ λ \lambda λ
∮ S D ⋅ d S = ∫ F ∖ R c D ⋅ d S + ∫ F ∖ R c D ⋅ d S + ∫ M ∖ R c D ⋅ d S = λ l \oint_{S} \mathbf{D} \cdot d\mathbf{S} = \int_{\mathbf{F} \setminus \mathbf{R}^{c}} \mathbf{D} \cdot d\mathbf{S} + \int_{\mathbf{F} \setminus \mathbf{R}^{c}} \mathbf{D} \cdot d\mathbf{S} + \int_{\mathbf{M} \setminus \mathbf{R}^{c}} \mathbf{D} \cdot d\mathbf{S} = \lambda l ∮ S D ⋅ d S = ∫ F ∖ R c D ⋅ d S + ∫ F ∖ R c D ⋅ d S + ∫ M ∖ R c D ⋅ d S = λ l 在上、下底面处, 面元 dS 与 D 的夹角为 π / 2 \pi/2 π /2
∫ Mom D ⋅ d S = D ∫ Mom d S = 2 π r l D = λ l \int_{\text{Mom}} \mathbf{D} \cdot d\mathbf{S} = D \int_{\text{Mom}} dS = 2\pi r l D = \lambda l ∫ Mom D ⋅ d S = D ∫ Mom d S = 2 π r l D = λ l 所以 D = λ 2 π r D = \frac{\lambda}{2\pi r} D = 2 π r λ D = ε E D = \varepsilon E D = εE
E = D ε = λ 2 π ε 0 ε r r E = \frac{D}{\varepsilon} = \frac{\lambda}{2\pi\varepsilon_0\varepsilon_r r} E = ε D = 2 π ε 0 ε r r λ 于是再由式(5.3.8)得到两极间的电势差为
U 12 = ∫ R 1 R 2 E ⋅ d l = λ 2 π ε 0 ε r ln R 2 R 1 U_{12} = \int_{R_1}^{R_2} \mathbf{E} \cdot d\mathbf{l} = \frac{\lambda}{2\pi\varepsilon_0\varepsilon_r} \ln \frac{R_2}{R_1} U 12 = ∫ R 1 R 2 E ⋅ d l = 2 π ε 0 ε r λ ln R 1 R 2 因此得出单位长度柱形电容器的电容为
C = λ λ 2 π ε 0 ε r ln R 2 R 1 = 2 π ε 0 ε r ln ( R 2 / R 1 ) C = \frac{\lambda}{\frac{\lambda}{2\pi\varepsilon_0\varepsilon_r} \ln\frac{R_2}{R_1}} = \frac{2\pi\varepsilon_0\varepsilon_r}{\ln(R_2/R_1)} C = 2 π ε 0 ε r λ ln R 1 R 2 λ = ln ( R 2 / R 1 ) 2 π ε 0 ε r (5.7.5)
从以上计算可以看出,电容器的电容决定于电容器本身的结构,几何尺寸和填充的电介质的介电特性,与电容器所带电荷量
图 5-52 圆柱形电容器
无关。电容器定义式显示,电容器两极上的电荷量变化与电压变化的关系,电容表示升高单位电压所需的电荷量。所需的电荷量越多,说明容电能力越强。正像给水桶蓄水,上升单位高度所需的水越多,则水桶的容量也就越大。
在计算电容时,总是随意地给某个极板赋予电荷量,并未考虑"击穿"问题。而任何实际电容器都有一个额定电压,这就限制了电荷量随意地增加。因为当电荷量(电压)达到一定程度时,电容器内部电场会增加,致使电介质被击穿,电容器就会变成一个导体了。
5.7.3 静电场的能量
要使电容器两极分别充以 ± Q \pm Q ± Q
W = ∫ d W = ∫ 0 Q q C d q = Q 2 2 C W = \int dW = \int_0^Q \frac{q}{C} dq = \frac{Q^2}{2C} W = ∫ d W = ∫ 0 Q C q d q = 2 C Q 2 即外力做功 W 引起电容器中贮存的能量 W. 变化,故有
W e = Q 2 2 C = 1 2 C U 2 = 1 2 Q U W_e = \frac{Q^2}{2C} = \frac{1}{2}CU^2 = \frac{1}{2}QU W e = 2 C Q 2 = 2 1 C U 2 = 2 1 Q U (5.7.6)
以平行板电容器为例,当将平行板电容器相关参量代入上式,可以看出,电能实际贮存于电场之中。对平行板电容器(不计
入边缘效应), C = ε 0 ε r S d C = \frac{\varepsilon_0 \varepsilon_r S}{d} C = d ε 0 ε r S Q = S σ Q = S\sigma Q = S σ E = σ ε 0 ε r E = \frac{\sigma}{\varepsilon_0 \varepsilon_r} E = ε 0 ε r σ
W e = 1 2 ε 0 ε r E 2 S d ( 5.7.7 ) W_e = \frac{1}{2} \varepsilon_0 \varepsilon_r E^2 Sd \qquad (5.7.7) W e = 2 1 ε 0 ε r E 2 S d ( 5.7.7 ) 式中,Sd 是电容器两极板间的体积。
上式表明,电容器的充电过程中外力所做的功,形成了电容
图 5~53 静电场的能量
器空间中的电场,转化成电场能量,由此得出单位体积中的电能——电场能量密度。
w e = 1 2 ε E 2 (5.7.8) w_e = \frac{1}{2} \varepsilon E^2 \tag{5.7.8} w e = 2 1 ε E 2 ( 5.7.8 ) 式中, ε = ε 0 ε r \varepsilon = \varepsilon_0 \varepsilon_r ε = ε 0 ε r
虽然上面的推理是针对平行板电容器,但结论是普遍的,如果电场是均匀的,电场中贮存的能量等于电场能量密度 w e w_e w e w e w_e w e
W e = ∫ V w e d V = ∫ V 1 2 ε E 2 d V ( 5.7.9 ) W_{e} = \int_{V} w_{e} dV = \int_{V} \frac{1}{2} \varepsilon E^{2} dV \qquad (5.7.9) W e = ∫ V w e d V = ∫ V 2 1 ε E 2 d V ( 5.7.9 ) 式中,dV是体积元,E 为场强函数,积分遍及整个电场所在区域。
例题 5-14
计算半径为 R,带电荷量为 Q 的导体球在真空中的静电场能。
导体球外电场强度 E = Q 4 π ϵ 0 r 2 e r ( r > R ) E = \frac{Q}{4\pi\epsilon_0 r^2} e_r(r>R) E = 4 π ϵ 0 r 2 Q e r ( r > R )
解:导体内电场强度为零,利用高斯定理得
径为 r、厚度为 dr 的球壳为体积元,则 d V = 4 π r 2 d r dV = 4\pi r^2 dr d V = 4 π r 2 d r
W e = ∣ V w e d V = ∣ V 1 2 ε E 2 d V W_{e} = ∣_{V} w_{e} dV = ∣_{V} \frac{1}{2} \varepsilon E^{2} dV W e = ∣ V w e d V = ∣ V 2 1 ε E 2 d V = ∫ R ∞ 1 2 ε 0 ( Q 4 π ε 0 r 2 ) 2 4 π r 2 d r = \int_{R}^{\infty} \frac{1}{2} \varepsilon_{0} \left( \frac{Q}{4\pi \varepsilon_{0} r^{2}} \right)^{2} 4\pi r^{2} dr = ∫ R ∞ 2 1 ε 0 ( 4 π ε 0 r 2 Q ) 2 4 π r 2 d r = Q 2 8 π ε 0 R =\frac{Q^2}{8\pi\varepsilon_0 R} = 8 π ε 0 R Q 2 静止的电荷,在其周围仅仅激发电场, 但是,当电荷相对观察者运动时,对于观察 者来说,他不仅能够测量出该电荷所产生的 电场,而且还测量到另外的一种场——磁 场。第六章将对磁场进行讨论。
思考题与习题
5.1 在一个带正电的大导体附近 A 点,放置一检验电荷 q 0 q_0 q 0 q 0 q_0 q 0 q 0 q_0 q 0 q 0 q_0 q 0 F / q 0 F/q_0 F / q 0 q 0 q_0 q 0
5.2 已知两电荷连线的中点处场强为零,试问 这两个电荷的电荷量和符号如何?
5.3 试讨论下列问题:
(1) 当闭合曲面内的电荷的代数和等于零时,是不是闭合曲面上任一点的场强一定为零?为什么(用电偶极子来说明)?
(2) 在应用高斯定理求场强时,应该怎样选择高 斯面。
5.4 如图所示,在一个均匀分布着正电荷的球面外,放置了一个电偶极子,其电矩 p。方向如图,问:
当将它释放后,它将如何运动?
5.5 在一个等边三角形的三个顶角处各放置一个电荷,电荷的大小性质都相同,如果以这三角形的中心为球心,作一个包围这三个电荷的球形高斯面,问:
(1) 能否利用高斯定理求出它们所产生的场强?
(2) 高斯定理是否仍然成立?
5.6 举例说明以下问题:
(1) 场强大的地方,电势是否一定高? 电势高的 地方是否场强大?
(2) 场强为零的地方电势是否一定为零? 电势为零的地方,场强是否一定为零?
(3) 场强大小相等的地方,电势是否相等?等势面上的场强大小是否相等?
5.7 (1) 若已知某点的电势,可以确定该点的电场强度吗?
(2) 若某两点有相同的电势,则介于它们间的各处的电场强度必为零吗?
5.8 带有相同正电荷的两个相邻导体之间可否 有电势差?
5.9 当一带电物体移近一个导体壳时,带电体本身在导体壳内产生的电场是否为零? 而静电屏蔽的效应是如何发生的?
5.10 一个孤立导体球带电荷量为 Q,其表面场 强沿什么方向? Q 在其表面上的分布是否均匀? 其表 面是否等电势? 导体内任意点 P 的场强是多少?
5.11 如图所示,一半径为 R 不带电导体球 A,球中有两个球形空腔,假设在各空腔中心分别放置点电荷 q 1 q_1 q 1 q 2 q_2 q 2 ( r ≫ R ) (r \gg R) ( r ≫ R ) q 0 q_0 q 0 q 1 q_1 q 1 q 2 q_2 q 2
12 (1) 电位移 D 是否只与自由电荷 q 0 q_0 q 0
(2) 若高斯面上电位移 D 的通量为零,是否面上 E 一定为零?
5.13 电介质的电极化与导体的静电感应,两者的微观过程有何不同?
5.14 如图所示,在一个有限大的均匀电介质球的球心处,有一点电荷+q。试问:
(1) 球内某点 A 处的场强 E λ E_{\lambda} E λ q 4 π ϵ λ ϵ λ t 2 \frac{q}{4\pi\epsilon_{\lambda}\epsilon_{\lambda}t^{2}} 4 π ϵ λ ϵ λ t 2 q
(2) 球外某点 B 处的场强 E n E_n E n q 4 π ε 0 ε r r a 2 \frac{q}{4\pi\varepsilon_0\varepsilon_r r_a^2} 4 π ε 0 ε r r a 2 q
15 在由一定电荷分布形成的均匀电场 E 0 E_0 E 0 E 0 E_0 E 0 ε \varepsilon ε E 0 E_0 E 0 E 0 E_0 E 0
5.16 两个孤立导体,当带有相同电荷量时,具有不同电势,问哪一个具有较大的电容?
5.17 将一个接地的导体球 A 移近一个孤立导体 B,B 的电势升高还是降低?
5.18 如图所示,用电源给平行板电容器充电后,再将开关S断开,然后准静态地移近两极板,在此过程中外力做正功还是负功?外力的方向与静电力的方向是相同还是相反?电容器贮能增加还是减少?
5.19 在上题中,如果充电后不切断 S,而移近两极,情况如何?
5.20 两绝缘导体 A ∖ B A \setminus B A ∖ B A ∖ B A \setminus B A ∖ B U A B U_{AB} U A B
5.21 依玻尔氢原子模型,计算电子在半径为 5.3 × 10 − 11 5.3 \times 10^{-11} 5.3 × 1 0 − 11
5.22 如图所示,两个质量都是 m 的相同的小球,带等量同号电荷 q,各用长为 l 的丝线悬挂于同一点,由于库仑斥力,两悬线夹角为 θ \theta θ θ \theta θ sin θ \sin\theta sin θ tan θ \tan\theta tan θ
(1) 两球距离 x 与 q l l m 的关系;
(2) 若两个球上的电荷以 d q d t \frac{dq}{dt} d t d q
23 如图所示,一电荷 q 1 = 1.0 × 10 − 6 q_1 = 1.0 \times 10^{-6} q 1 = 1.0 × 1 0 − 6 q 2 = 2.0 × 10 − 6 q_2 = 2.0 \times 10^{-6} q 2 = 2.0 × 1 0 − 6
5.24 如图所示,两个正的点电荷,电荷量相等,相距为 2a,通过两电荷连线做一中垂面,试求此面上场强最大点的轨迹。
5.25 如图所示,有半径为 R 的半圆形线,分别 求在下列情况下,圆心处的电场强度为 E。
(2) 电荷线密度 λ = λ 0 cos θ , λ 0 \lambda = \lambda_0 \cos \theta, \lambda_0 λ = λ 0 cos θ , λ 0 α \alpha α θ \theta θ O α O\alpha O α
26 长 l = 15 cm 的带电线 AB,如图所示均匀 分布着线密度 λ = 5 × 10 − 6 \lambda = 5 \times 10^{-6} λ = 5 × 1 0 − 6 -1 的电荷。试求:
(1) 在带电线的延长线上与 B 端相距 R=5 cm 处 P 点的场强;
(2) 在 AB 线垂直平分线上与 AB 线中点相距 R=5 cm 处 O 点的场强。
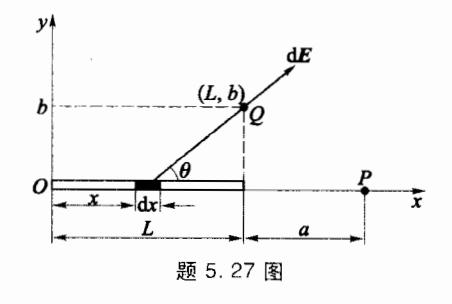
5.27 如图所示,一长为 L 的带电细棒,沿+z 轴放置,其一端位于原点,电荷线密度 λ = λ 0 z ( λ 0 ) \lambda = \lambda_0 z (\lambda_0) λ = λ 0 z ( λ 0 )
(1) 在 x 轴上, x = L + a(a) 为不为零的常量)处的场强;
(2) 坐标为(L,b)处的场强(b)为大于零的常量)。
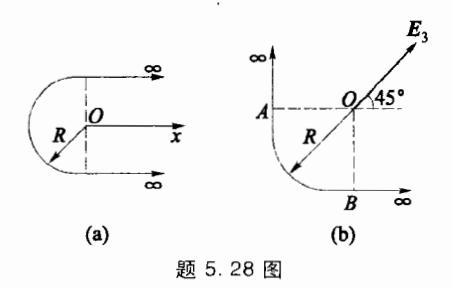
5.28 一根无限长均匀带电线,被弯曲成如图 所示的两种形状。如果该线的电荷线密度为 A,弧 形曲率半径为 R,分别求出两种情况下 O 点处的 场强。
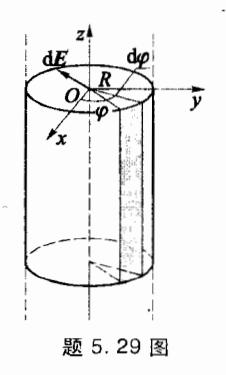
29 如图所示,一根无限长带电圆柱面处于柱 坐标系中,z 轴沿圆柱面轴向,电荷面密度 σ = σ 0 cos φ \sigma = \sigma_0 \cos \varphi σ = σ 0 cos φ σ 0 \sigma_0 σ 0
5.30 如图所示,电场强度 ∣ E ∣ = ∣ E z i ∣ = A x 1 2 |E| = |E_z i| = Ax^{\frac{1}{2}} ∣ E ∣ = ∣ E z i ∣ = A x 2 1 A = 800 N ⋅ C − 1 A = 800 \text{ N} \cdot \text{C}^{-1} A = 800 N ⋅ C − 1
(2) 若正方体的边长为 10 cm,它的表面所包围的总电荷量为多少(图中 a 点坐标为 100 cm);
5.31 一半径为 R 的带电球体,电荷体密度 ρ = ρ 0 ( 1 r R ) \rho = \rho_0 \left(1 \frac{r}{R}\right) ρ = ρ 0 ( 1 R r ) ρ 0 \rho_0 ρ 0
(1) 球内、外的电场分布;
(2) 电场强度的最大值及其所对应的位置。
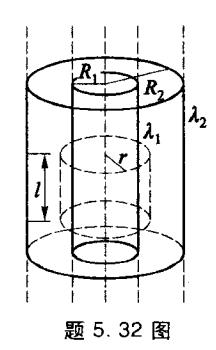
32 如图所示,半径分别为 R 1 R_1 R 1 R 2 R_2 R 2 λ 1 \lambda_1 λ 1 λ 2 \lambda_2 λ 2
(1) 各区域内场强分布;
(2) 若 λ i = − λ 2 \lambda_i = -\lambda_2 λ i = − λ 2
5.33 在电荷体密度为 ρ \rho ρ O ∖ O ′ O\setminus O' O ∖ O ′
(1) O、O'、A、B 点的场强:
(2) 证明小球内是均匀场。
题 5.33图
5.34 一厚度为 b 的无限大均匀带电平板,平板 内均匀带电,电荷体密度为 ρ。求板内、外场强分布。
5.35 据量子力学的理论, 氢原子中心是一个带 正电荷 q. 的原子核(相当于一个正的点电荷), 外面 是带负电的电子云, 在正常状态下电子云的电荷体密
度分布为 ρ = − q e π a 0 3 e − 2 r a 0 \rho = -\frac{q_e}{\pi a_0^3} e^{-\frac{2r}{a_0}} ρ = − π a 0 3 q e e − a 0 2 r a 0 a_0 a 0
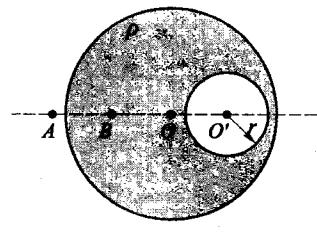
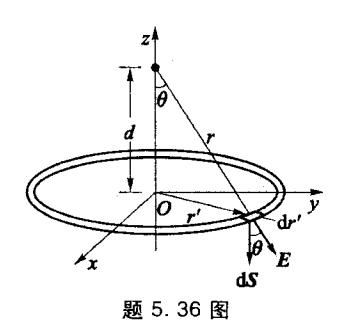
5.36 如图所示,一个 q = 5.0 × 10 − 7 q = 5.0 \times 10^{-7} q = 5.0 × 1 0 − 7
5.37 有一均匀电场,场强方向自左向右。把一个带电荷量为 q = 3 × 10 − 9 q=3\times10^{-9} q = 3 × 1 0 − 9 6 × 10 − 5 6\times10^{-5} 6 × 1 0 − 5 4.5 × 10 − 5 4.5\times10^{-5} 4.5 × 1 0 − 5
38 如图所示, AB = 2l, OCD 是以 B 为中心, l 为半径的半圆, A 点有正电荷 q, B 点有负电荷 -q。求:
(1) 把单位正电荷从 O 点沿 OCD 移到 D 点,电场力对它做了多少功?
(2) 把单位负电荷从 D 点沿 AB 的延长线移到无穷远处,电场力对它做了多少功。
5.39 氢原子的质子处于坐标原点,将电子从点(0.05,0,0)移到点(0.5,0.3,0)电场力做功多少?(坐标单位为nm,分别依功的定义和电势差概念计算。)
5.40 如图所示,有一长为1、带电荷量为0的均 匀带电杆,将它水平放置,求:
(1) 离杆右端 z0 处 A 点电势是多少?
(2) 若在该处放一点电荷 q,电势能是多少?
(3) 杆的中垂面上距杆为 a 的 B 点的电势。
5.41 空间有球对称的无限电荷分布,电荷体密 度 ρ = k r − 1 2 , k \rho = kr^{-\frac{1}{2}}, k ρ = k r − 2 1 , k
5.42 用积分法求均匀带电球壳的电场中任意 一点的电势(壳内、壳上、壳外)。
5.43 由半径为 a 的均匀带电球壳的电势 V= V 4 π ϵ 0 r ( r ≥ a ) \frac{V}{4\pi\epsilon_0 r}(r \ge a) 4 π ϵ 0 r V ( r ≥ a )
5.44 已知某空间区域的电势函数 V = x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 V = x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 + x^2 V = x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2 + x 2
(2) 坐标点(2,2,3)的电势及其与原点的电 势差。
5.45 一对无限长共轴直圆筒,半径分别为 R,和 R2,简面上均匀带电,内外简面单位长度上分别带电 荷量为+λ和-λ。求圆筒面间的电势分布及两筒间的 电势差。
放置,其间距为 d ( d v ‾ v ‾ ) d(d \, \overline{v} \, \overline{v}) d ( d v v ) σ \sigma σ B × C B \times C B × C B × C B \times C B × C
(1) B、C 板上的感应电荷;
(2) 空间各区间场强及电势分布。
5.47 一半径为 R 的金属球壳在离球心为 r(r> R)处放一点电荷,电荷量为q。求:
(2) 现格球壳接地,试确定其上的感应电荷为 多少?
5.48 两个极薄的同心导体球壳 A、B 半径分别 为 R A ∖ R B ( R A < R B ) R_A \setminus R_B(R_A < R_B) R A ∖ R B ( R A < R B )
5.49 如图所示,有一很大的带电金属薄板,另 外有一小球,质量 m = 1.0 × 10 − 3 m=1.0\times10^{-3} m = 1.0 × 1 0 − 3 q = 2.0 × q=2.0\times q = 2.0 × σ \sigma σ
题 5.49 图
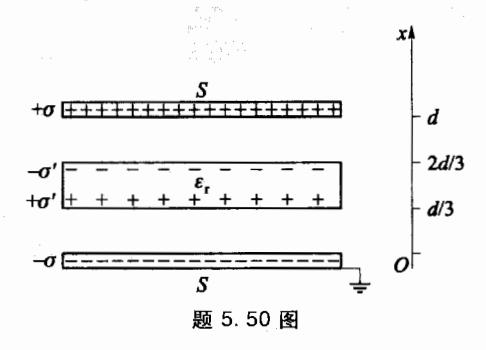
5.50 如图所示,平行板电容器两极板相距 d,在 正中对称处放一相对介电常量为 ε r \varepsilon_r ε r
(1) 极板各处的 P、E、D;
(2) 极板间各处电势分布(设一极板接地);
(3) 若极板面积为 S,电容为多少?
(4) 束缚电荷面密度为多少?
(5) 若介质板换成同样尺寸的金属板,电容为多少? 并与无介质或金属板时的电容做一比较。
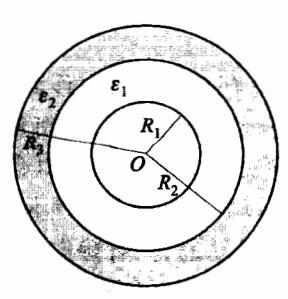
5.51 如图所示,一球形电容器由半径为 R 1 R_1 R 1 R 2 R_2 R 2 ϵ 1 \epsilon_1 ϵ 1 ϵ 2 \epsilon_2 ϵ 2 ϵ 2 \epsilon_2 ϵ 2 ϵ 1 \epsilon_1 ϵ 1
(2) 当内球带电-Q 时,各界面处束缚电荷的面密度 σ ′ \sigma' σ ′
题 5.51 图
5.52 如图所示,两块边长为 a 的正方形导体板构成电容器,相互间倾角为 θ \theta θ θ \theta θ C = ϵ 0 a 2 l ( 1 − a θ 2 l ) C = \frac{\epsilon_0 a^2}{l} \left(1 - \frac{a\theta}{2l}\right) C = l ϵ 0 a 2 ( 1 − 2 l a θ )
5.53 半径为 R, 带电荷量为 Q 的导体球, 周围充满相对介电常量为 ε \varepsilon ε
5.54 如图所示,一电容器极板是边长为 a 的正 方形,间距为 d,带电荷量为 ± Q \pm Q ± Q ϵ \epsilon ϵ
题 5.54 图