メインコンテンツまでスキップ

5.5 静电场中的导体

导电能力极强的物体称为导体。金属、石墨、电解液(酸、碱、盐的水溶液或熔液)等,都是导体。本节所涉及的导体特指固态的金属物体。

△ 文档:静电场中的导体

金属中原子的外层价电子,与原子核的联系较弱,它们很容 易脱离原子核的束缚。失掉价电子的原子成为正离子。金属中 正离子排列成有规则的晶格,形成金属的骨架,决定着金属的大 小和形状。而脱离原子核束缚的价电子,可以在晶格中自由运 动,故称为自由电子。自由电子在晶格中的分布类似于气体分子 的运动,故也称其为电子气。大量自由电子的存在是金属结构的 重要特征。当导体不带电时,导体中大量的自由电子所带的负电 荷与构成晶格的正离子所带的正电荷相中和,所以呈电中性。

当导体置于静电场中,情况又将怎样呢?

5.5.1 静电平衡条件​

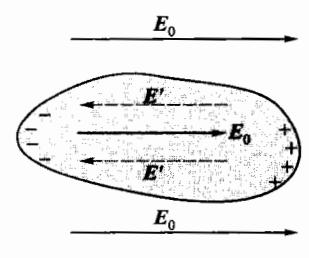
图 5-31 静电平衡

将一金属导体放入静电场 E0E_0 中, 开始时导体内的自由电子 在外电场 E。的作用下,将逆着外电场的方向移动,结果导体的一 端(图 5-31 左端)逐渐堆积起带负电荷的自由电子,而导体的另 一端,由于缺少电子逐渐呈现过剩的正电荷。这些电荷称为感应 电荷。这些感应电荷又在导体内部建立起一个附加的电场 E', 其方向恰好与外电场相反,对电子的进一步移动起到了阻碍的作 用。随着导体两端正、负电荷的积累逐渐增多,附加电场 E'也逐 渐加大,当附加电场的大小与外电场的大小相等时,导体内部的 电场强度 E 为零,即

E=E0+E′=0(5.5.1)E = E_0 + E' = 0 (5.5.1)

式(5.5.1)称为导体的静电平衡条件。静电平衡的过程进行得 很快,几乎瞬时即成。满足上式的状态称为静电平衡态,其特点 是导体内部场强处处为零,在表面电场没有切向分量。导体内部 及表面都无电荷的定向移动,即电流为零。

5.5.2 静电平衡导体的性质​

达到静电平衡的导体具有如下性质:

  • (1) 导体是等势体,导体表面是等势面。假设导体不是等势 体,有电势的变化就有不为零的电场,在导体内部电场的驱使下, 电荷就会继续定向移动,所以,达到静电平衡的导体是等势体,其 表面是等势面。
  • (2) 导体内部没有净电荷的分布,电荷只分布于导体的外表 面。由于导体内部的场强处处为零,所以在导体内任选高斯面上

电场强度通量也必然为零,根据高斯定理,导体内部的净电荷一定为零,因此导体所带净电荷只能分布在导体的外表面上。

  • (3) 导体外表面附近的场强垂直于导体表面。导体表面是一个等势面,等势面与电场线处处正交。由此可知,导体达到静电平衡时,导体外表面的场强垂直于导体表面。
  • (4) 在处于静电平衡的导体外,无限趋近于导体表面处场强 E∗E_* 与该处导体表面的电荷面密度 σ\sigma 的关系为
E18=σε0en(5.5.2)\boldsymbol{E}_{\frac{1}{8}} = \frac{\boldsymbol{\sigma}}{\varepsilon_0} \boldsymbol{e}_{n} \tag{5.5.2}

式中, ene_n 为到体面的外法线矢量。图 5-32 为任意形状的导体,现取一底面积 ΔS\Delta S 的小圆柱形高斯面,其一底面位于导体内,另一底面位于导体表面外且无限靠近表面处,圆柱面包围的电荷 σΔS\sigma \Delta S ,根据高斯定理便可得出式(5.5.2)。

需要说明的是,尽管从形式上看,式(5.5.2)似乎表示导体外表面附近的场强大小 E∗E_* 仅与其对应的导体某一局部表面上的电荷面密度 σ\sigma 有关,但这不意味着 E∗E_* 就是仅仅由 E∗E_* 处的 σ\sigma 产生的,式(5.5.2)是在电场线与表面垂直下得出的,这只能由所有电荷共同产生。

(5) 孤立导体处于静电平衡时,其表面电荷的分布是与导体 形状有关的,曲率半径小处,电荷密度大。

如图 5-33 所示,有两个大小不同的导体球 A、B,导体球半径分别为 RAR_A 、 RBR_B 。设 A 球大于 B 球,即 RAR_A > RBR_B ,它们彼此相距甚远,相互无影响。当用导线将它们连接后,再使它们带电。此时两球各自带电荷量为 qAq_A 、 qBq_B ,并且电荷均匀地分布在两个球的表面上,设各自电荷面密度分别为 σA\sigma_A 、 σB\sigma_B 。 在静电平衡时,两球的电势相等,有

VA=qA4πε0RA=VB=qB4πε0RBV_{A} = \frac{q_{A}}{4\pi\varepsilon_{0}R_{A}} = V_{B} = \frac{q_{B}}{4\pi\varepsilon_{0}R_{B}}

又因

σA=qA4πRA2,σB=qB4πRB2\sigma_{A} = \frac{q_{A}}{4\pi R_{A}^{2}}, \quad \sigma_{B} = \frac{q_{B}}{4\pi R_{B}^{2}}

于是得到电荷在两球间分布的关系为

σAσB=RBRA\frac{\sigma_{\rm A}}{\sigma_{\rm B}} = \frac{R_{\rm B}}{R_{\rm A}}

该结果说明,达到静电平衡后的孤立导体,其电荷面密度与表面曲率半径有关。在导体表面凸出,曲率较大(曲率半径较小)的尖锐地方,电荷面密度较大;若导体表面曲率较小,则电荷面密度较小;在表面凹进去,曲率为负的地方,电荷面密度更小。

图 5-32 导体表面场强

图 5-33 表面电荷密度与曲率 关系

图 5-34 "电风车"

图 5-35 电风

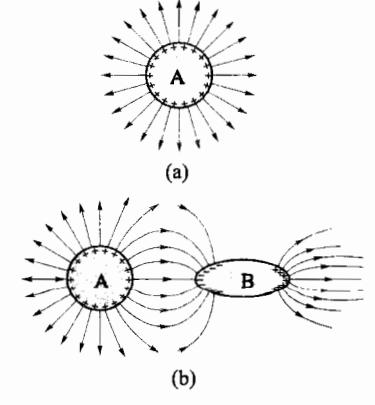
图 5-36 导体表面电荷分布与周围导体有关

当导体外表面尖锐处积累的电荷太多时,就会引起尖端放电,即导体尖端附近的强大电场对空气中游离的带电离子发生作用,使得电性与导体尖端为同号的离子远离尖端而去,而电性与尖端相异的离子则被尖端吸引。当带异号电性的离子被吸引到尖端上,放电后,又带上了与尖端同号的电荷而远离尖端,同性电荷在飞离过程中又会与空气分子碰撞,使空气分子进一步电离,产生更多的带电离子。此时的导体尖端仿佛是一个向外喷射电荷的喷枪,所喷射的电荷形成了"电风"。图 5-34 与图 5-35 就是尖端放电的例子。

尖端放电不仅使宝贵的电能白白损失掉,而且有时还会造成危险。因此,在制造高压输电线时,要尽量将导线表面处理得光滑些;在制造高压设备时,尽量去掉棱角,将高压电极做成球状。当然,尖端放电还有可以利用的一面,例如制造各种电子点火器就需要将电极做得尽可能尖锐些;再如避雷针就是利用尖端放电而达到保护建筑物避免雷击的目的。

以上所述的电荷面密度随曲率变化规律,仅仅适用于孤立导体[图 5-36(a)]。如果一个导体附近还存在着其他带电体[图 5-36(b)],那么导体表面的电荷分布,将由导体本身及附近带电体共同决定。静电平衡时导体内场强为零的性质,必然要求 A 上的电荷重新分布,B 两端也会出现感应电荷。

5.5.3 静电屏蔽​

如图 5-37(a) 所示,将导体空腔放入任意静电场时,空腔外表面会出现相应的感应电荷。空腔外表面电荷的分布,总是要使导体空腔内电场强度始终为零。电场线将垂直指向导体空腔外表面的某一部分上,同时又从导体空腔的另一部分外表面垂直出发,导体空腔的内侧始终没有电场线穿过。利用导体空腔这一性质,可以将某些物体或仪器放在各种导体空腔内,以避免外电场

图 5 07 热电量类

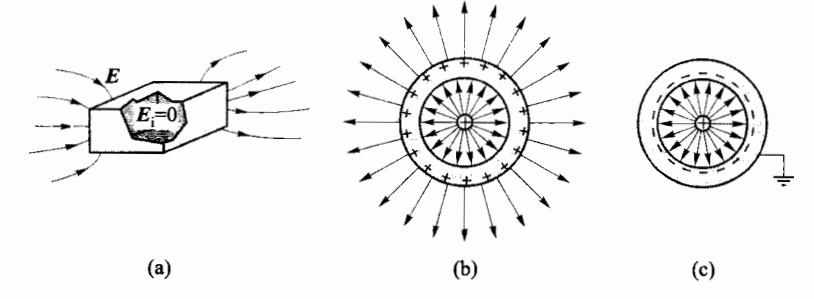
对它们的影响,这种技术称为静电屏蔽。在实际应用中,用金属 网来代替金属空腔一样能达到很好的屏蔽效果。例如有许多信 号线为了保证所传输的弱信号不被外电场干扰,在它外面用金属 丝网包围起来,这种线叫屏蔽线。

当导体空腔包含带电体时,为使空腔内、外壁间金属层的场强为零,会在空腔内、外壁上产生等量感应电荷[图 5-37(b)], 当外壁接地时(地为零电位)腔内带电体的电场不会影响到外部 [图 5-37(c)],这样同样能达到屏蔽的目的。为了防止高压、高频电器设备对周围空间产生影响,常常用接地的金属网将它们屏蔽起来。

例题 5-12​

如图 5-38 所示,面积为 S,相距很小的两平行导体板 A、B,分别带电荷量为 QAQ_A 、 QBQ_B 。求两板各表面的电荷分布。

解:设导体板 A 左右两表面的电荷面密度 分别为 σ1\sigma_1 、 σ2\sigma_2 ,导体板 B 左右两表面的电荷 面密度分别为 σ3\sigma_3 、 σ4\sigma_4 ,由电荷守恒定律有

σ1S+σ2S=QA(1)\sigma_1 S + \sigma_2 S = Q_A \tag{1} σ3S+σ4S=QR(2)\sigma_3 S + \sigma_4 S = Q_{\rm R} \tag{2}

两平行导体板的四个表面,相当于四个平行放置的"无限大"带电薄板,依式(5.2.10),每个薄板在其周围所产生的电场强度的大小均为 E=σ/(2ε0)E = \sigma/(2\varepsilon_0) ,则空间任意点的场强应为各板在该点产生场强的叠加。由导体静电平衡条件,导体 A 和 B 内部场强为零,应用场强的叠加原理,在导体 A 和 B 内部,任意点处 a、b 的场强有

σ42ε0+σ22ε0+σ32ε0−σ12ε0=0(3)\frac{\sigma_4}{2\varepsilon_0} + \frac{\sigma_2}{2\varepsilon_0} + \frac{\sigma_3}{2\varepsilon_0} - \frac{\sigma_1}{2\varepsilon_0} = 0 \tag{3} σ12ε0+σ22ε0+σ32ε0−σ42ε0=0(4)\frac{\sigma_1}{2\varepsilon_0} + \frac{\sigma_2}{2\varepsilon_0} + \frac{\sigma_3}{2\varepsilon_0} - \frac{\sigma_4}{2\varepsilon_0} = 0 \tag{4}

联立式(1)-(4),解得

\sigma_{1} = \sigma_{4} = \frac{Q_{A} + Q_{B}}{2S} \\ \sigma_{2} = -\sigma_{3} = \frac{Q_{A} - Q_{B}}{2S} \end{array} \right\} \tag{5}$$ ![](../_page_190_Picture_14.jpeg) 图 5-38 例题 5-12图 由式(5)可知,对于一对较大的平行导体板来说,在静电平衡时,导体板的相对表面上(即 2、3 面)总是带等量异号电荷;两导体板相背表面(即 1、4 面)总是带等量同号电荷。 有几种具体情况,现讨论如下: - (1) 若两导体板带有等量异号电荷时,即 $Q_A = -Q_B = Q$ ,即两板带有等量异号电荷时,由式(5) 得 $\sigma_1 = \sigma_4 = 0$ , $\sigma_2 = -\sigma_3 = \frac{Q}{S}$ ,此时两板相背面上无电荷分布,电荷只分布在两导体板相对面上,电场垂直于导体板,仅均匀分布于两导体板之间。 - (2) 若两导体板带有等量同号电荷时,即 $Q_A = Q_B = Q$ ,由式(5)得 $\sigma_2 = \sigma_4 = \frac{Q}{S}$ , $\sigma_2 = -\sigma_3 = 0$ ,电荷只分布在两导体板相背面上,两导体板 之间电场强度为零,电场垂直导体板,仅分 布于两导体板之外的空间。 (3) 若两个导体板中仅有其中一个带有静电荷,例如 $Q_A = Q_1Q_2 = 0$ ,由式(5)有 $\sigma_1 = \sigma_4 = \frac{Q}{2S}$ , $\sigma_2 = -\sigma_3 = \frac{Q}{2S}$ , B 板上出现了感应电荷,此时两导体板之间和两导体板之外的空间均有电场分布。 #### 例题 5-13 如图 5-39 所示,半径为 $R_1$ 的金属小球带电荷量 Q,放在内外半径分别为 $R_2$ 、 $R_3$ 的金属球壳内,球壳带电荷量 Q。试求: (1)两球间的电势差及球壳内外表面带电荷量;(2)若将小球与大球接触,情况又当如何? 解:(1) 利用球形对称性,在 $R_1$ 与 $R_2$ 之间作一同心球形高斯面,利用高斯定理可得导体球与导体球壳间的电场强度为

E = \frac{Q}{4\pi\varepsilon_0 r^2} e_r

据此可以得出导体球与导体壳间的电势差为 据此可以得出导体球与导体壳间的电势 差为

U_{12} = \int_{R_1}^{R_2} \mathbf{E} \cdot d\mathbf{l} = \frac{Q}{4\pi\varepsilon_0} \left( \frac{1}{R_1} - \frac{1}{R_2} \right)

在球壳内的金属层中作一高斯面(图5−39中的虚线)包围球壳内表面,有 在球壳内的金属层中作一高斯面(图 5-39 中的虚线)包围球壳内表面,有

\oint_{S} \mathbf{E} \cdot d\mathbf{S} = \frac{1}{\varepsilon_{0}} \sum_{i} q_{i} = \frac{1}{\varepsilon_{0}} (Q + Q_{\mu})

式中, $Q_{h}$ 表示导体球壳的内表面上因感应 ![](../_page_191_Picture_14.jpeg) 图 5-39 例题 5-13图 出现的静电荷。因为导体内场强 $E_{\rm p}=0$ ,所以球壳内表面带电荷量 $Q_{\rm p}=-Q$ ,对球壳有 $Q=Q_{\rm p}+Q_{\rm p}$ ,所以 $Q_{\rm p}=Q-Q_{\rm p}=2Q$ 。因为 $\frac{1}{R_1}-\frac{1}{R_2}>0$ ,故只要 Q 为正电荷, $U_{12}$ 就一定为正值。如小球带正电,则它的电势一定比导体球壳的电势高,且与外球壳所带电荷量无关。 (2) 当小球与大球接触时,它们为等势体,电势差为零,小球所带的电荷全部分布到大球壳的外表面上,外表面带电荷量仍为 2Q。