My object has been, first to discover correct principles and then to suggest their practical development. ( James Prescott Joule)
热力学第一定律确定了系统在状态变化过程中内能变化、功和热量之间的关系。下面利用热力学第一定律讨论理想气体在 等体、等压和等温过程中的能量转化情形。


文档:典型热力学过程

NOTE
4.2.1 等体过程
若系统在状态变化过程中体积始终保持不变,该过程就称为等体过程,理想气体的等体过程的过程方程可写为 V=C1 或 p/T=C2(C1,C2 均为常量)。准静态等体过程在 p-V 图上是一条垂直于横轴的有向线段,图 4-4 所示为从状态 A(p1,V,T1) 到状态 B(p2,V,T2) 的等体过程。
在等体过程中,体积V不变,即dV=0,系统对外做功为
W=∫pdV=0(4.2.1)
系统内能改变为
ΔE=Mm2iR(T2−T1)
(4.2.2)
系统吸热为
QV=MmCV,m(T2−T1)
(4.2.3)
根据热力学第一定律,这里 Qv=ΔE ,所以
CV,m=2iR
(4.2.4)
可见,理想气体的摩尔定容热容 CVm 是一个与分子自由度有关的物理量。引入 CVm 后,理想气体的内能增量经常表示为
ΔE=MmCV,m(T2−T1)
(4.2.5)
4.2.2 等压过程
若系统在状态变化过程中压强始终保持不变,该过程就称为等压过程,等压过程的过程方程可写为 p=C,或 T/V=C(C)
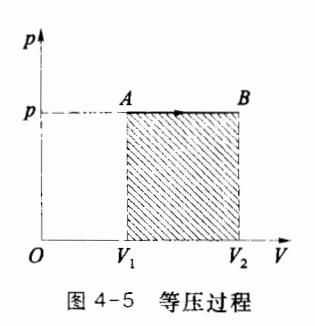
常量)。理想气体的准静态等压过程在 p-V 图上是一条平行于横轴的有向线段,如图 4-5 所示为从状态 A(p,V1,T1) 到状态 B(p,V2,T2) 的等压过程。
在准静态等压过程中,理想气体对外界做功为
W=∫V1V2pdV=p∫V1V2dV=p(V2−V1)
(4.2.6)
这一关系也可由 p-V 图中等压过程曲线与横轴间的矩形面积得出,若过程中气体体积被压缩,则需在矩形面积值前加一负号。
因内能增量 ΔE 与过程无关,只决定于系统的始末状态,在 等压过程前后系统内能增量仍为
ΔE=MmCν,m(T2−T1)
(4.2.7)
在等压过程中系统吸收的热量为
Qp=MmCp.m(T2−T1)
(4.2.8)
由热力学第一定律 Q=W+ΔE , 所以
MmCp,m(T2−T1)=p(V2−V1)+MmCV1m(T2−T1)
将理想气体物态方程 pV=MmRT 代入上式,经过化简可得
Cp,m=R+Cv,m
(4.2.9)
该式称为迈耶公式,它给出了理想气体的摩尔定压热容 Cν,m 和摩尔定容热容 Cν,m 所满足的关系。
(4.2.9) 对于任意的热力学过程,怎么计算 C._和摩 热容量?
4.2.3 等温过程
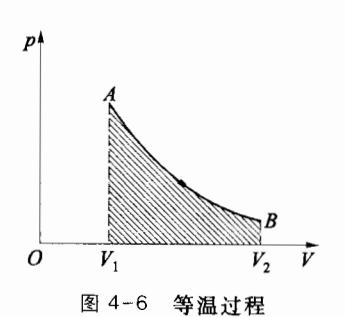
若系统在状态变化过程中温度始终保持不变,该过程就称为等温过程,等温过程的过程方程可写为 T=C1 ,或 pV=C2(C1,C2) 均为常量)。理想气体的准静态等温过程在p-V图上是一条反比例函数曲线,图 4-6 所示为从状态 A(p1,V1,T) 到状态 B(p2,V1,T) 的等温过程。
在等温过程中, dT =0,理想气体内能增量为零,即 ΔE =0。 在准静态等温过程中系统对外做功为
W=∫v1v2pdV=∫v1v2MmRTVdV
由于过程中T不变,所以有
W=MmRTlnV1V2=MmRTlnp2p1
(4. 2. 10)
根据热力学第一定律,气体在等温过程中吸收的热量为
QT=W=MmRTlnV1V2=MmRTlnp2p1
(4. 2. 11)
可见,在等温过程中,气体从外界吸收的热量全部用来对外做功。
妈题 4-1
一定量的氧气(可视为刚性双原子分子理想气体)经历如图 4-7 所示的三个等值过程:由初态 A 开始,先做等压膨胀,使其体积增大至原来的两倍;然后对其等体加热,使压强增加一倍,最后做等温膨胀,变化到与初态压强相同的末态 D。试求各等值过程中气体吸收的热量 Q、对外做的功 W、内能增量 ΔE 及气体在整个过程中吸收的热量。若气体由初态 A 开始,只经历等压膨胀过程到达末态 D,该过程中的 Q、W 和 ΔE 又各是多少?

图 4-7 例题 4-1 图
① 等压过程 A→B
①等压过程 A→B
WAB=pA(VB−VA)
=1.013×105×(2−1)×10−3 J=1.01×102 J
ΔEAB=MmCV,m(TB−TA)=Mm25R(TB−TA)
=25(pBVB−pAVA)=25pA(VB−VA)
=25×1.013×102 J=2.53×102 J
QAB=WAB+ΔEAB=1.01×102 J+2.53×102 J
=3.54×102 J
或利用
QAB=MmCp,m(TB−TA)=Mm27R(TB−TA)
=27pA(VB−VA)
=27×1.013×105×(2−1)×10−3 J
=3.54×102 J
② 等体过程 B→C
QBC=ΔEBC=MmCV,m(TC−TB)=Mm25R(TC−TB)
=25VB(pC−pB)
=25×2×10−3×(2−1)×1.013×105 J
=25×2×10−3×(2−1)×1.013×105 J
=5.07×102 J
③ 等温过程 C→D
ΔEco=0
WRC=0
QCD=WCD=MmRTClnVCVD=pCVClnpDpC
=2×1.013×105×2×10−3ln1×1.013×1052×1.013×105 J
=2.81×102 J
④ 整个过程 $A \rightarrow B \rightarrow C \rightarrow D$
WAB=WAB+WBC+WCD=3.82×102 J
ΔE总=ΔEAB+ΔEBC+ΔECD=7.60×102 J
Q总=QAB+QBC+QCD=1.14×103 J
(2) 若只经历等压膨胀过程 A→B→D
由式 pCVC=pDVD 得
pCVC
VD=pDpCVC=2VC=4VA
该过程中
W=pA(VD−VA)=pA(4VA−VA)=3pAVA
=3×1.013×105×1.0×10−3 J=3.04×102 J
ΔE=MmCV,m(TD−TA)=Mm25R(TD−TA)
=25pA(VD−VA)=25×3pAVA
=25×3×1.013×105×1.0×10−3 J
=7.60×102 J
Q=ΔE+W=1.06×103 J
或
Q=MmCp,m(TD−TA)=Mm27R(TD−TA)
=1.06×103 J
比较(1)和(2)的结果可看出,由某初态出发,经历不同的热力学过程到达相同的末态,系统内能增量相同,而吸收的热量与对外界所做的功因过程不同各异。

