4.1 热力学第一定律

4.1.1 准静态过程

我们知道, 当系统不受外界影响时它将处于确定的平衡态。 一旦有外界作用,系统原有的平衡状态将遭到破坏。系统由一个 平衡态经历一系列中间状态变化到另一平衡态,我们说系统经历 了一个热力学过程(简称过程)。一般情况下,过程进行得较快, 系统在尚未达到新的平衡前就进行了下一步变化,这样,过程中 系统经历的是一系列非平衡状态,这种过程称为非静态过程。但 是,由于非平衡态的问题比较复杂,因此,在热力学中,常假想一 种在过程进行中的每一时刻系统都处于平衡态的过程,称为准静 态过程。显然,准静态过程是一种理想过程,因为过程要想发生, 系统的状态必须发生变化,否则过程不可能发生。假设在过程开 始前系统处于某平衡态,过程一旦发生,系统原有的平衡状态必 将遭到破坏,随着过程的进行,系统状态不断地发生着变化,因 此,实际发生的过程不可能由一系列平衡状态构成,即实际过程 绝非准静态过程。但是,对于实际过程来说,如果过程进行得非 常缓慢,可以认为,在过程中的每时每刻,系统都来得及恢复平 衡,在整个过程中,系统所经历的每一个中间状态都非常接近平 衡态,这样的热力学过程可看作是准静态过程。

如果系统在进行准静态过程时和外界之间没有摩擦,则该过程称为无摩擦的准静态过程。在进行无摩擦的准静态过程时,系统所受的外界作用力与气体对外界的作用力相等,因此可以用描述系统的物理量替代外界相应的量,从而方便问题的讨论。

构成准静态过程的每一个平衡态都可在 p-V 图上用一个点表示,因此一个准静态过程可以在 p-V 图上用一条曲线表示。即一个准静态过程总可以对应 p-V 图中的一条曲线,反过来,p-V 图中的一条曲线也总可以找到与之对应的一个准静态过程。如图 4-1 所示为一个任意准静态过程所对应的曲线,其中圆点代表某一平衡态 A。对于非静态过程来说,由于包含非平衡态,而系统处于非平衡态时没有确定的宏观性质,状态参量没有确定数值,因而非平衡态在 p-V 图中不能用确定的点表示,所以非静态过程在 p-V 图中也没有确定的曲线与之对应。

4.1.2 功 内能 热量

1. 准静态过程中功的计算

如图 4-2 所示,一定量的气体被封闭在气缸内,活塞可以在气缸内无摩擦地左右移动。假设在活塞移动过程中,气体所经历的过程为准静态过程。因活塞和气缸间无摩擦,所以气体所进行的是无摩擦的准静态过程,任意时刻活塞和气体间所互施的作用力都相等。设气体压强为p,体积为V,活塞面积为S。当活塞缓慢地移动一微小距离 dl 时,气体对外界所做的元功为 dW = Fdl = pSdl,即

$$dW = pdV \tag{4.1.1}$$

式中 dV 是当活塞移动微小距离 dl 时气体体积的微小变化。当气体由体积 $V_1$ 膨胀到 $V_2$ 时,它对外做功为

$$W = \int_{V_1}^{V_2} p \, \mathrm{d}V \tag{4.1.2}$$

若 $W>0$ ,表示系统对外界做正功; $W<0$ ,表示系统对外做负功,或外界对系统做正功。

气体在准静态过程中的功在 p-V 图中可由准静态过程曲线下的面积表示,图 4-3(a) 中曲线 AB 与横轴之间的面积表示在 $A \rightarrow B$ 过程中气体对外所做的功,图中画斜线的窄条的面积表示在体积发生 dV 变化时气体对外所做的元功。若只给定初、末状态,则气体可以由初始状态经历不同的准静态过程 [如图 4-3 (b) 所示的任意准静态过程 I 和 II ] 到达末态,显然,曲线 I 和 II 与横轴间的面积不等,即在两过程中气体做功的数值不同,所以功是与具体过程有关的量,是一个过程量。

2. 系统的内能

一个由大量分子(或原子)组成的系统即使没有整体的宏观

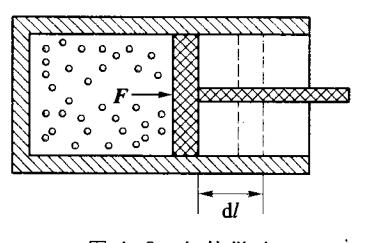
图 4-2 气体做功

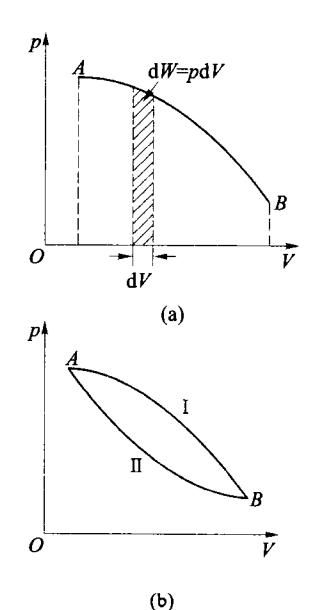
图 4-3 做功与过程有关

运动,系统内仍具有一定的能量,称为内能,包括分子间的相互作用能,分子热运动能量,以及分子中所含的其他微观粒子的动能和相互作用能等。在本章中,由于不涉及微观粒子的性能和结构的变化,所以热力学系统的内能是组成它的全部分子热运动能量(平动、转动、振动)和分子(或原子)间相互作用势能的总和。内能是状态量,当系统处于一定的平衡态时,内能具有确定值。当系统状态改变时,内能作相应变化。系统由某平衡态变化到另一平衡态,不论经历怎样的过程,内能的改变量总是一定的。

由气体动理论知,理想气体分子间没有相互作用,理想气体的内能就是组成系统的所有分子能量的总和。质量为m、摩尔质量为M的理想气体在温度为T的平衡状态的内能为

$$E = \frac{m}{M} \cdot \frac{i}{2}RT \tag{4.1.3}$$

由上式知,理想气体内能只是温度的单值函数。当系统由温度为T,的平衡态变化到温度为T,的平衡态时,内能的改变量为

$$\Delta E = E_2 - E_1 = \frac{m}{M} \cdot \frac{i}{2} R(T_2 - T_1) = \frac{m}{M} \cdot \frac{i}{2} R \Delta T \quad (4.1.4)$$

对于实际气体来说,分子间存在相互作用,因此,分子间距离的变化将导致分子间相互作用势能的改变,所以实际气体的内能除与温度有关外,还与系统体积(或压强)有关。

3. 热量

大量实验事实说明,当系统和外界间温度不同时,将有能量在二者间转移,从而使系统的状态发生变化,在此过程中传递的能量就是热量。热量和功一样是一个过程量。一般情况下,对于给定的初态和终态,系统经历的过程不同,吸收的热量也不同。

热量一般用符号 Q 表示,在国际单位制中,热量的单位是 J (焦耳),它和另一个单位"cal(卡)"的关系为

$$1 \text{ cal} = 4.186 \text{ J}$$

对于摩尔质量为 M,质量为 m 的系统,当温度发生微小变化,由 T 变化到T+dT 时,它所吸收的热量为

$$dQ = \frac{m}{M}C_{m}dT \qquad (4.1.5)$$

式中, $C_m$ 称为物质的摩尔热容,它的含义是:1 mol 的物质温度每升高或降低1 K 所吸收或放出的热量。

当温度由 $T_1$ 变化到 $T_2$ 时,系统吸收的热量为

$$Q = \int_{T_1}^{T_2} \frac{m}{M} C_{m} dT$$

(4.1.6)

对于理想气体,一般来说,摩尔热容与温度有关,当温度变化

范围不大时,可将摩尔热容视为常量,则上式写为

$$Q = \frac{m}{M} C_{m} (T_{2} - T_{1}) = \frac{m}{M} C_{m} \Delta T$$

(4.1.7)

因为热量与过程有关, 摩尔热容也与过程有关, 过程不同, 摩 尔热容也不同。在热力学中我们用得最多的摩尔热容有两个,它 们是摩尔定压热容 $C_{\nu}$ 和摩尔定容热容 $C_{\nu}$ ,分别指系统在压 强和体积保持不变过程中的摩尔热容。