

文档:理想气体压强公式
NOTE
根据气体动理论,封闭在容器中的一定量的气体,其所有分 子都在做不规则热运动,气体内壁不停地受到气体分子的碰撞。 就单个分子来说,它何时、以什么角度、用多大的力对器壁进行碰 撞完全是偶然的。所以,从微观上看,器壁受到的是一次次间断 的、不规则的冲击。但从大量分子整体来看,宏观上,气体作用在 器壁上的却是一个连续的力。气体的压强就是这种力的作用引 起的,在数值上等于单位时间内与单位面积器壁碰撞的所有分子 总冲量的统计平均值。
3.3.1 理想气体微观模型
理想气体是一种最简单的热力学系统,是实际气体在压强不 太高、温度不太低情况下的理想化、抽象化结果。从微观上看,当 仅考虑分子质心的运动时,理想气体具有如下特点:
- (1) 分子本身的大小远小于分子之间的距离,因此分子可看 作质点;
- (2) 由于分子力的作用距离很短,除碰撞的一瞬间外,分子 从微观上看,温度和压强的意义是 之间及分子与器壁间的相互作用可忽略不计;
- (3) 分子之间及分子与器壁间的碰撞是完全弹性的。
什么?
3.3.2 压强的微观解释
在推导理想气体压强公式时,对处于平衡状态下的理想气体 我们还假设:① 重力的影响忽略不计,即认为容器内任意位置的 分子数密度(单位体积内的分子数)均相等;② 任意时刻,分子沿 任意方向运动的概率相等。
考虑一棱长为l的立方体容器(图 3-3),里面贮有N个质量为m的同种理想气体分子。考虑到在平衡状态时,容器器壁各处压强相同,所以任选器壁的一个面,例如选择与x轴垂直的 A1 面,计算其所受的压强。
首先分析一个分子的运动对器壁的冲力。任选一个分子 i,其速度为 vi ,在如图直角坐标系中, vi 沿 x、y、z 三个坐标轴的分量的大小分别为 vix 、 viy 、 viz 。 当分子 i 与器壁 A1 面碰撞时,由于碰撞是完全弹性的,所以,该分子沿 x 轴方向的速度分量由 vix 变为 −vix ,而沿 y 轴和 z 轴方向的速度分量不变,因此,在碰撞过程中该分子的动量增量为
Δpi=Δpix=−mvix−mvix=−2mvix
此动量增量来自于器壁对它的冲量,所以一次碰撞中该分子对器壁的冲量为 2mvix 。分子 i 与 A1 面碰撞后被弹回并飞向与 A1 面相对的 A2 面,与 A2 面发生弹性碰撞后又回到 A1 面进行碰撞(应当注意,分子 i 在 A1 面和 A2 面之间运动时,可能会与其他分子碰撞,但由于质量相等的质点做完全弹性碰撞时交换速度,故就气体整体来说,可等价为分子 i 由器壁的一个面直接飞到另一面)。由此可见,分子 i 相继两次与 A1 面碰撞所需时间为 2l/vix ,因此,单位时间内分子 i 对 A1 面撞击的次数为 vix/2l ,而一次碰撞对器壁的冲
量为 2mvix , 所以,单位时间内,分子 i 对 A1 面的冲量为 2lvix⋅2mvix=2l2mvix2 , 也即分子 i 对 A1 面的平均冲力为
Fix=2l2mvix2=lmvix2
实际上,容器中有N个分子,N个分子对器壁 A1 面的总的平均冲力为
Fx=i=1∑NFix=i=1∑Nlmvix2
根据压强的定义,压强p是作用在容器器壁单位面积上的平均冲力,所以
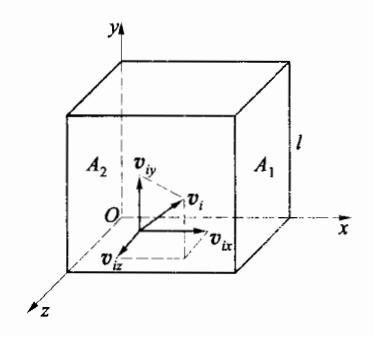
图 3-3 理想气体压强公式推导 示意图
p=l2Fx=l21i=1∑NFix=i=1∑Nl3mvix2=l3mNN∑i=1Nvix2
Nvix21=Nvix2i=1∑Nvix2 表示容器内 N 个分子沿 x 轴方向的速度分量平方的 平均值,因此压强可写为
p=l3mNvx2=VNm vx2=nm vx2
式中, n=VN 为单位体积内的分子数,即分子数密度。由于处于平 衡状态时,气体分子在任意时刻、沿任意方向运动的概率相等,因 此,对容器中的所用气体分子来说,有 vx2=vy2=vz2=vz2 。所以
戈
p=31nmv2
p=32nεki(3.3.1)
式中, ϵkl=21mv2 是气体分子的平动动能的平均值,称为平均平均 动能。式(3.3.1)即为理想气体的压强公式,该式表明,理想气 体压强的大小与气体分子数密度 n 和分子的平均平动动能 ϵn 成 正比。气体分子数密度越大,压强越大;分子平均平动动能越大, 压强也越大。由于 n 和 ϵl 是微观量的统计平均值,因此宏观可 观测量p也是一个统计量。

