1.4 动量定理与动量守恒定律

本节讨论的是从牛顿第二定律导出的第二个定理和守恒律。

1.4.1 动量定理

1. 质点的动量定理

人们在日常生活中有这样的经验,即使在钉子上面放上一个质量很大的锤子,也很难将钉子压进木头里去。可是如果挥动锤子,使其具有一定速度,就很容易将钉子打进去。锤子质量越大、速度越大,打进钉子就越容易。这使人想到需要将质量与速度联系起来描写物体的运动,因此提出了动量的概念。牛顿第二定律式(1.2.1)解释了力与动量变化的关系。将式(1.2.1)改写为

$$\mathbf{d}\boldsymbol{p} = \boldsymbol{F} \mathbf{d}t \tag{1.4.1}$$

式中Fdt称为元冲量。两边积分得

$$p_2 - p_1 = \int_{t_1}^{t_2} F dt \tag{1.4.2}$$

上式左边是质点从 $t_1$ 到 $t_2$ 整个时间间隔内动量的变化,其中的 $p_1 = mv_1$ 是质点 $t_1$ 时刻的动量, $p_2 = mv_2$ 是质点 $t_2$ 时刻的动量。 上式右边的积分定义为力 F 从 $t_1$ 到 $t_2$ 时间间隔内的冲量,记为

$$I = \int_{t_1}^{t_2} \mathbf{F} \, \mathrm{d}t \tag{1.4.3}$$

在国际单位制中,冲量的单位为 N·s(牛顿秒),与动量的单位量纲相同。

合并式(1.4.2)和式(1.4.3),得

$$I = \int_{t_1}^{t_2} F dt = p_2 - p_1 = m v_2 - m v_1 \tag{1.4.4}$$

此式表明,质点所受合外力的冲量等于质点动量的增量,这一结论称为质点的动量定理。它是以积分表示的,称为质点动量定理的积分形式。

动量是状态量,物体处在某一状态下,具有确定的速度,也就 具有确定的动量。而冲量是过程量,是力作用一段时间过程产生 的,不能说成某一时刻力的冲量。质点的动量定理给出了质点在 一段运动过程中,状态量的改变与相关过程量的关系(这是与质 点的动能定理类似但含义不同的另一种关系)。动量和冲量都是 矢量。动量的增量是末态动量与初态动量的矢量差,一般情况下 它不仅有数值的变化,也有方向的变化。冲量是描写力对时间累 积作用的物理量。这种累计应是 Fdt 在给定时间段的矢量和,而 不是将力F的大小与时间间隔的简单相乘。在力F的方向随时 间不断改变的情况下,冲量的方向不是某一瞬时力F的方向,而 是质点动量增量的方向。来看一个特殊的例子,质点做勾束圆周 运动一周,末态动量与初态动量相等,动量的增量为零,按照动量 定理,在这个过程中,向心力F,的冲量等于零。这个冲量等于 零,不是向心力等于零,也不是不经历时间,而是向心力对时间的 累积等于零。实际上在这个过程中,各个微小时间段内向心力的 元冲量 $F_{a}$ dt 首尾相接形成了一个闭合的圆,其矢量和为零。

将质点的动量定理矢量式(1.4.4)在坐标轴上投影,可得到动量定理沿该坐标轴的分量式。以直角坐标系为例,有

$$\begin{cases} I_{x} = \int_{t_{1}}^{t_{2}} F_{x}\,dt = mv_{x2} - mv_{x1} \\ I_{y} = \int_{t_{1}}^{t_{2}} F_{y}\,dt = mv_{y2} - mv_{y1} \\ I_{z} = \int_{t_{1}}^{t_{2}} F_{z}\,dt = mv_{z2} - mv_{z1} \end{cases} \tag{1.4.4}$$

能用物理原理说明"以柔克刚"的 道理吗?

在应用分量式时必须注意各分力、分速度本身的正负号。

动量定理常用于碰撞、打击等问题中,在这类问题中,物体间相互作用时间很短而作用力变化很快且数值很大,这种力称为冲力。冲力的方向一般是不变的,但大小较难测定。对于一维问题,在实际中,往往用冲力的平均值F乘以作用时间 $\Delta t$ 作为冲量的近似值,将动量定理写成

$$\overline{F}\Delta t \approx m v_2 - m v_1 \tag{1.4.6}$$

用此式可以进行简单的数值计算。

2. 质点系的动量定理

设有一个由n个质点组成的质点系,其中第i个质点的质量为 $m_i$ ,初态 $t_1$ 时刻速度为 $v_{i1}$ ,末态 $t_2$ 时刻速度为 $v_{i2}$ ,所受来自系统外物体的合外力为 $F_i$ ,来自系统内其他质点的合内力为 $F_{p_i}$ 。对第i个质点应用动量定理,有

$$\int_{t_1}^{t_2} (\boldsymbol{F}_i + \boldsymbol{F}_{pq_i}) dt = m_i \boldsymbol{v}_{i2} - m_i \boldsymbol{v}_{i1}$$

将上式对质点系内所有质点求和,有

$$\int_{t_1}^{t_2} \left( \sum_{i=1}^n \mathbf{F}_i + \sum_{i=1}^n \mathbf{F}_{\mu_i} \right) dt = \sum_{i=1}^n m_i \mathbf{v}_{i2} - \sum_{i=1}^n m_i \mathbf{v}_{i1} \tag {1.4.7}$$

先看等式左边,由于系统内所有内力都是成对的作用力与反作用力,它们大小相等方向相反,而且相互作用的时间相同,因此,内力的总冲量为零,即 $\int_{t_1}^{t_2} \sum_{i=1}^n F_{\mu_i} dt = 0$ 。再看等式右边, $\sum_{i=1}^n m_i v_{i2}$ 为质点系的末态动量,令 $\mathbf{p}_2 = \sum_{i=1}^n m_i v_{i2}$ ; $\sum_{i=1}^n m_i v_{i1}$ 为质点系的初态动量,令 $\mathbf{p}_1 = \sum_{i=1}^n m_i v_{i1}$ 。于是,式(1.4.7)写成

$$\int_{t_1}^{t_2} \sum_{i=1}^{n} \mathbf{F}_i dt = \mathbf{p}_2 - \mathbf{p}_1 = \Delta \mathbf{p} \tag{1.4.8}$$

此式表明:质点系所受合外力的冲量等于质点系动量的增量。这 称为质点系的动量定理。

应该注意,质点系的动量定理中不包含内力的冲量;而质点系的动能定理中则包含内力所做的功。原因在于,冲量是力对时间的累积作用,时间是单向的,成对内力的冲量彼此抵消为零;功是力对空间的累积作用,位移是矢量,具有方向性,成对内力的功不一定会被抵消。这是二者的重要区别。另外,像质点的动量定理一样,质点系的动量定理仅适用于惯性系。

1.4.2 动量守恒定律

如果质点系所受的合外力为零,即 $\sum_{i=1}^{n} F_{i} = 0$ ,根据式 (1.4.8),有 $p_{2} = p_{1}$ ,或 $p = \sum_{i=1}^{n} m_{i}v_{i} = 常矢量。这可表述为: 当质 点系所受的合外力为零时,质点系的总动量保持不变。这称为动量守恒定律。$

关于动量守恒定律的几点注意事项:① 动量守恒定律仅适用于惯性系;② 动量守恒定律的条件是系统所受的合外力为零。但当内力远远大于外力且作用时间较短时,外力影响很小,可以近似地应用动量守恒定律,如爆炸、碰撞等情形就是如此;③ 在有多个外力作用的过程中,尽管动量守恒的条件不能满足,但如果合外力沿某个方向的分量等于零,则在该方向上仍然可以应用动量守恒定律;④ 动量守恒定律是自然界最普遍的规律之一,不但适用于经典力学,也适用于高速与微观的情况。

1.4.3 碰撞

碰撞是一种常见的现象。碰撞的一个突出特点就是碰撞力很大,碰撞时间很短,可以忽略外力(例如重力)对碰撞物体运动的影响,从而应用动量守恒定律。

碰撞过程中物体间的相互作用是很复杂的。简单说来,在碰撞的开始阶段,碰撞物体间的内力做功,使物体发生形变转化为弹性势能;在碰撞的结束阶段,物体的形变复原使弹性势能转化为碰撞物体的动能。碰撞物体材料的性质决定了形变复原的程度及弹性势能的大小,同时也就决定了碰撞系统机械能是否守恒。据此,可将碰撞分为三种类型,具体讨论如下。

1. 完全弹性碰撞

考察光滑桌面上两个小球的对心碰撞,碰撞前、后两个小球均沿一条直线运动。如图 1-30 所示,质量为 $m_1$ 的小球碰前速度为 $v_{10}$ ,碰后速度为 $v_{11}$ ;质量为 $m_2$ 的小球碰前速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度为 $v_{20}$ ,碰后速度,如后,如后,这个位,如后,这个位,如后,这个位,如后,这个位,如后,这个位,如后,这个位,如后,这个位,如后,这个位,如后,这个位,这个位,这个位,这个位,这个位,这个位,这个位,这个位,这个位,这个位

图 1-30 完全弹性碰撞

$$m_1 v_{10} + m_2 v_{20} = m_1 v_1 + m_2 v_2$$ $$\frac{1}{2} m_1 v_{10}^2 + \frac{1}{2} m_2 v_{20}^2 = \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2$$

以上两式就是解决完全弹性碰撞的基本关系式。联立两式,可以得出 $v_1$ 和 $v_2$ 的表达式(这里从略),还可以得到如下一个有用的公式:

$$v_2 - v_1 = v_{10} - v_{20} \tag{1.4.9}$$

此式表明,两球碰撞后的分离速度等于碰撞前的趋近速度。

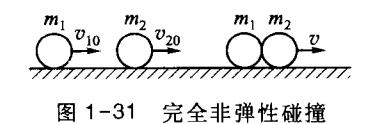
2. 完全非弹性碰撞

仍然考察光滑桌面上两个小球的对心碰撞,碰撞前、后两个小球均沿一条直线运动。如图 1-31 所示,质量为 $m_1$ 的小球碰前速度为 $v_{10}$ ,质量为 $m_2$ 的小球碰前速度为 $v_{20}$ ,碰后两球结合在一起,以共同速度 v 运动。由于作用于系统的合外力为零,因而系统动量守恒;但是发生完全非弹性碰撞时,物体的形变完全不能复原,造成能量损失,所以机械能不守恒,对应这里就是动能不守恒。动量守恒关系式为

$$m_1 v_{10} + m_2 v_{20} = (m_1 + m_2) v$$

依据此式可进行相关计算。

3. 非完全弹性碰撞

这是介于上面二者之间的情况。碰撞时物体的形变仅有部分复原,虽然可以彼此分开,但机械能有一定损失。因此仅有动量守恒成立,仿照第一种碰撞的假设,有

$$m_1 v_{10} + m_2 v_{20} = m_1 v_1 + m_2 v_2 \tag{1.4.10}$$

另外,由于有动能损失,式(1.4.9)变为 $v_2 - v_1 < v_{10} - v_{20}$ ,这表明两球碰撞后的分离速度小于碰撞前的趋近速度。为了描述物体形变的复原程度,定义分离速度与趋近速度之比为恢复系数,记为e,表示为

$$e = \frac{v_2 - v_1}{v_{10} - v_{20}} \tag{1.4.11}$$

恢复系数的大小与发生碰撞的两物体的材料性质有关,其值可以通过实验测定。将待测定的两种材料(当然也可以是同种材料)分别制成小球和厚重的平板。令小球自高度 H 自由下落到处于水平位置的平板上,测出小球反弹的高度 h。以竖直向下为坐标轴正方向,小球与平板碰撞前的速度 $v_{10} = \sqrt{2gH}$ ,碰撞后反弹速度 $v_1 = -\sqrt{2gh}$ ;厚重平板碰撞前静止, $v_{20} = 0$ ;碰撞后,由于质量很大,可近似认为不动,即 $v_2 \approx 0$ 。将各速度值代人式(1.4.11),有

$$e = \frac{-v_1}{v_{10}} = \frac{\sqrt{2gh}}{\sqrt{2gH}} = \sqrt{\frac{h}{H}} \tag{1.4.12}$$

可见,只要测出H与h就能求出e值。

从恢复系数 e 的定义式(1.4.11)可以看出,当 e=1 时,有 $v_2-v_1=v_{10}-v_{20}$ ,正是式(1.4.9),对应完全弹性碰撞;当 e=0 时,有 $v_2=v_1$ ,对应完全非弹性碰撞;当 $0<e<1$ 时,对应非完全弹性碰撞。 前两种碰撞恰为两个极限情况,给出了 e 值的边界。后一种碰撞对应 e 值的一个区间。也可以说,式(1.4.11)涵盖了碰撞的三种类型。将式(1.4.11)与动量守恒关系式(1.4.10)联立,可以解出碰撞后两球的速度:

$$v_{1} = v_{10} - \frac{m_{2}(1+e)(v_{10} - v_{20})}{m_{1} + m_{2}}, \quad v_{2} = v_{20} + \frac{m_{1}(1+e)(v_{10} - v_{20})}{m_{1} + m_{2}}\tag{1.4.13}$$

上式不仅适用于非完全弹性碰撞,而且当 e=1 时,可以给出完全弹性碰撞的结果;当 e=0 时,也可以给出完全非弹性碰撞的结果。所以式(1.4.13)给出的是各种对心碰撞结果的通式。

以上讨论的是一维对心碰撞的情况,下面来看一个简单的二维非对心碰撞的例子。如图 1-32 所示,在光滑水平桌面上建立二维直角坐标系。质量为 $m_2$ 的小球开始处于静止状态且位于坐标原点,质量为 $m_1$ 的小球以大小为 $v_{10}$ 的速度沿 x 轴向 $m_2$ 运动。设两个小球发生碰撞时稍有偏心(图中没有画出),则碰撞后两个小球的速度矢量不共线。设碰撞后小球 $m_1$ 的速度大小为 $v_1$ ,方向与 x 轴夹角为 $\theta_1$ ;碰撞后小球 $m_2$ 的速度大小为 $v_2$ ,方向与 x 轴夹角为 $\theta_2$ 。由于系统所受合外力为零,所以动量守恒。将系统动量分别沿 x、y 两个坐标轴投影,得到

$$\begin{cases} m_1 v_{10} = m_1 v_1 \cos \theta_1 + m_2 v_2 \cos \theta_2 \\ 0 = -m_1 v_1 \sin \theta_1 + m_2 v_2 \sin \theta_2 \end{cases} \tag{1.4.14}$$

如果碰撞是完全弹性的,则有机械能守恒,对应这里就是动能守恒,即

$$\frac{1}{2}m_1v_{10}^2 = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2 \tag{1.4.15}$$

这样,共有三个方程。一般说来, $m_1$ 、 $m_2$ 和 $v_{10}$ 是已知的,需要求的是 $v_1$ 、 $\theta_1$ 和 $v_2$ 、 $\theta_2$ 共四个未知数。显然,问题是无解的。实际上还需要通过观测,如果能得到四个未知数中的一个,问题就能解决。

*1.4.4 火箭飞行简介

火箭飞行是动量定理及守恒律的应用实例。火箭依靠自身

图 1-32 二维碰撞

携带的燃料和氧化剂在燃烧室内燃烧,产生的高温、高压气体从 尾部喷出,喷出气体的反冲力就是火箭的推动力。

为简单计,假设火箭在离地很远的某段区域内沿直线飞行,此时地球的引力和空气阻力的影响很小可以忽略。以地球为参考系,沿火箭飞行方向取坐标轴。设 t 时刻,火箭的质量为 m,速度为 v。此后在 dt 时间内,火箭喷出气体的质量为 -dm(注:dm 本身为负值),喷出气体相对火箭的速率为 $v_r$ ,火箭速度增量为 dv。在 t+dt 时刻,火箭的质量为 m+dm,速度为 v+dv,喷出气体相对地球的速度是 $v+dv-v_r$ 。由动量守恒定律,有

$$mv = (m+dm)(v+dv) + (-dm)(v+dv-v_r)$$

整理上式,得

$$dv = -v_r \frac{dm}{m} \tag{1.4.16}$$

设 $v_0$ 和 $m_0$ 为该级火箭在空中开始点火时的速度和质量,v 和 m'为该级火箭在燃料烧完时的速度和质量,在喷射速率 $v_r$ 保持不变的情况下,将式(1.4.16)积分

$$\int_{v_0}^{v} dv = -v_r \int_{m_0}^{m'} \frac{dm}{m}$$

得到

$$v = v_0 + v_r \ln \frac{m_0}{m'} \tag{1.4.17}$$

式中 $m_o/m'$ 称为火箭的质量比。式(1.4.17)表明,在喷射速率保持不变的情况下,火箭的速度增量与喷射速率成正比,与质量比的对数成正比。限于技术条件上的制约,仅靠单级火箭达到宇宙速度是困难的,采用多级火箭是提高速度的有效途径。多级火箭是由几个单级火箭首尾串接而成的,当第一级火箭燃料耗尽后,其壳体与主体脱离,第二级火箭点火进入工作状态,依此类推,最终达到所需的飞行速度。