1.2 牛顿运动定律

运动是物质本身的属性,运动学的任务是研究怎样描述运动情况。物体如何运动则取决于物体间的相互作用,研究物体间的相互作用,以及由此引起的物体运动状态变化的规律是动力学的任务。

从本节起开始讨论质点动力学问题。质点动力学的基本定律是牛顿运动定律,它是整个经典力学的基础。

1.2.1 牛顿运动定律的基本内容

牛顿在 1687 年出版的名著《自然哲学的数学原理》中,提出 了三条运动定律,这三条定律称为牛顿运动定律。

1. 牛顿第一定律

牛顿第一定律的表述为:任何物体,只要没有外力迫使它改变状态,都将保持静止或匀速直线运动状态。

第一定律引入了两个重要概念,即力和惯性。

第一定律给出了力的科学定义:力是一物体对另一物体的作

用,力的效果是使受作用的物体改变其运动状态。

第一定律提出了惯性的概念。当物体不受其他物体作用(或 其他物体对它的作用相互抵消)时,物体将保持静止或匀速直线 运动状态不变,即物体保持自己原来的运动状态不变是不需要其 他物体的作用的。可见,物体保持自己原来的运动状态不变是物 体自身具有的一种固有属性。物体保持原来的运动状态不变的 性质称为惯性。所以牛顿第一定律也称为惯性定律。

2. 牛顿第二定律

牛顿第二定律定量描述了外力与质点运动状态变化的关系。 牛顿第二定律的具体形式为

$$\boldsymbol{F} = \frac{\mathrm{d}\boldsymbol{p}}{\mathrm{d}t}, \quad \boldsymbol{p} = m\boldsymbol{v} \tag{1.2.1}$$

式中p是质点的质量与速度的乘积,叫作质点的动量。在国际单位制中,力的单位是 N(牛顿),质量的单位是 kg(千克),动量的单位是 kg·m/s(千克米每秒)。当质点质量不随时间变化时,牛顿第二定律成为 F=ma,在同样大小的力作用下,质量大的物体加速度小,状态不容易受到改变,因此质量是物体惯性大小的量度。在不同的坐标系中,F=ma 有相应的分量形式。例如,在直角坐标系中有

$F_x = ma_x$ , $F_y = ma_y$ , $F_z = ma_z$

在自然坐标系中有

$$F_{n} = ma_{n}$$

, $F_{n} = ma_{n}$

这些分量形式表明,某一方向的力只引起同一方向的加速度,说明相互垂直方向运动的独立性。

3. 牛顿第三定律

牛顿第三定律指明物体间的作用力具有相互作用的性质。

牛顿第三定律的表述为: 当物体 A 以力 F 作用在物体 B 上时, 物体 B 也必定同时以力 F 作用在物体 A 上, F 和 F 在同一条直线上, 大小相等而方向相反。其数学表达式为

$$\boldsymbol{F} = -\boldsymbol{F}' \tag{1.2.2}$$

牛顿第三定律又称为作用和反作用定律。从定律内容来讲, 应该注意:作用力和反作用力总是同时存在、同时消失、互为依存的;作用力和反作用力分别作用在两个物体上,两者不能互相抵消;作用力和反作用力是性质相同的力,如作用力是摩擦力,反作用力也是摩擦力,作用力是万有引力,反作用力也是万有引力。

研究物体运动学问题时,参考系的选择可以是任意的。但在研究动力学问题时,参考系的选择就不能任意了,因为牛顿运动定律并不是对所有参考系都能成立。例如,位于同一高度的 A、B

Every body continues in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed upon it.(Isaac Newton)

两物体同时自由下落,若分别以 A、B 为参考系来研究对方的运动,各自观察到的现象都是相对静止的。但两者确实都受重力作用,这与牛顿第一定律关于受力作用的物体会改变运动状态的结论相矛盾。而如果观察者是在以匀速率垂直下降的电梯中观察 A、B 的运动,则物体受重力作用加速下落,这与牛顿第一、第二定律是相符合的。因此,可以牛顿运动定律是否成立来定义一种参考系:凡牛顿运动定律成立的参考系称为惯性参考系,简称惯性系;反之,称为非惯性系。判断一个参考系是否为惯性系的最根本的方法,就是观察和实验。在地球上所进行的许多实验结果表明,在相当高的实验精度内,地球可以看作是惯性系。然而由于地球的自转和围绕太阳的公转,地球只是一个近似的惯性系。在天体运动的研究中,更精确的惯性系可选太阳——恒星参考系。有关惯性系与非惯性系的问题下面还有专题讨论。

牛顿运动定律是从大量实验事实总结概括出来的,它的正确性、可靠性已经得到了充分的验证。然而,近代科学的发展证明,它仅是在一定范围内适用的理论。只有当物体的运动速度远小于光速且在宏观的领域中,它才是正确的。当物体的运动速度接近光速或研究微观领域的问题时,则需要分别应用相对论力学和量子力学理论。

1.2.2 力学中常见的力

在牛顿运动定律中,我们讨论了力的一般概念以及力的作用效果,并未涉及力的具体形式和它们的特性。要想正确地分析解决力学问题,还必须掌握力学中常见的几种力的特点,这样才能正确地分析物体的受力情况,从而应用力学规律解决实际问题。

现代科学研究的结果已使人们认识到,可以把力按其本质的不同分为四种,即万有引力、电磁力、强相互作用和弱相互作用。前两种力在物体距离较大时仍能起作用,故称长程力;后两种力作用距离极短,故称短程力。对于以宏观物体的机械运动为研究对象的经典力学,所涉及的力只有万有引力和电磁力。

力学中常见的力主要有重力、弹性力和摩擦力。重力属于万有引力的范畴,弹性力和摩擦力从本质上看则是来源于物质内部分子间或原子间的电磁力。

1. 万有引力和重力

牛顿在对开普勒行星运动三定律进行了深入研究之后,提出了万有引力定律:质量分别为 $m_1$ 和 $m_2$ 的两个质点,相距为r时,

它们之间的引力与两者的质量乘积成正比,与两者之间的距离平 方成反比。在国际单位制中,万有引力表示为

$$F = G \frac{m_1 m_2}{r^2} \tag{1.2.3}$$

式中,比例系数 $G=6.67408(31)\times10^{-11}$ m³·kg⁻¹·s⁻²,称为引力常量。万有引力存在于宇宙万物之间,通常一般物体之间的万有引力极小,但对于天体来说,万有引力却是支配它们运动的主要动力。当计算两个星球之间的万有引力时,由于星球的线度远小于它们之间的距离,故可将其视为两个质点,式中的距离 r 指两个球心之间的距离。

应该指出,万有引力定律中出现的质量只决定着万有引力的大小,反映物体吸引其他物体的能力,因此称为引力质量。与此对应的是牛顿第二定律中出现的质量,前文已经述及,那里的质量反映物体惯性的大小,称为惯性质量。引力质量和惯性质量是在完全不同的两种物理现象中分别独立引入的,各自反映物质的不同属性。可以证明,任何物体的引力质量和惯性质量都相等,所以此后不再区分,统称质量。

地球表面附近的物体所受的重力,来源是万有引力,但有些许差异,原因是地球存在自转,有关此问题将在后面的非惯性系中加以讨论。当不考虑地球自转时,可认为二者相等。一般情况下,物体运动高度相比地球半径 R 而言很小可以忽略,以 m 和 m'分别表示物体和地球质量,则物体受到的重力大小为

$$P = mg \approx m \frac{Gm'}{R^2} \tag{1.2.4}$$

式中, $g \approx Gm'/R^2 = 9.81 \text{ m} \cdot \text{s}^{-2}$ ,称为重力加速度。重力的方向指向地心。

2. 弹性力

当物体之间因为相互接触而产生变形时,变形的物体试图恢复原状,物体之间便会有作用力产生,这种发生在相互接触的物体之间、与物体的变形相联系的力统称为弹性力。

弹簧受外力作用发生拉伸或压缩变形时,弹簧对施力物体的作用力称弹簧的弹性力。如以弹簧原长处作为坐标原点,沿弹簧拉伸或压缩方向建立 x 轴,则弹簧弹性力表示为

$$F = -kx \tag{1.2.5}$$

式中,k为弹簧的劲度系数,其值与弹簧的形状及材料性质有关; x为弹簧的形变量,可正可负;式中的负号保证了弹簧的弹性力始终指向弹簧原长所在点。

用绳索拉物体,绳索和物体间的拉力也是一种弹性力。当绳

索被拉伸时,其内部就会发生变形,因此会出现弹性力。如在绳内某点取一横截面,截面一侧必向另一侧施以拉力,我们把绳索内部某横截面两侧互施的拉力称为绳索在该横截面上的张力,常用符号 $F_{\rm T}$ 表示。当绳索的质量可以忽略不计时,绳内各截面处张力的大小相等并等于它两端的外力的数值。绳索作用于物体上的拉力总是沿着绳索的方向。

将一重物放在桌面上,由于重物压紧桌面,两者均有微小变形,因而互相施以弹性力。通常我们将重物作用于支撑面的弹性力称为压力,而将支撑面作用于重物的弹性力称为支持力或弹力。由于这种弹性力的方向总是垂直两者的交界面,所以也常称为正压力。物体间的正压力与支持力是一对作用力和反作用力,二者大小相等方向相反,分别作用于对方。

3. 摩擦力

两物体相互接触时,发生在接触面间的阻止物体相对运动或相对运动趋势的力称为摩擦力。只有相对运动趋势而无实际运动时的摩擦力称为静摩擦力;有相对运动时的摩擦力称为滑动摩擦力或简称动摩擦力。

静摩擦力的大小与外力有关。例如,一人用手去推水平地面上的木箱,当推力较小时,木箱不动。但此时木箱与地面之间有相对运动趋势,当属静摩擦力。这时地面对木箱的静摩擦力大小与外力在水平面上的分力相等,方向沿接触面并与木箱相对地面的运动趋势方向(即外力沿水平面上的分力方向)相反。增加推力但仍不足以使木箱运动时,地面对木箱的静摩擦力大小随之增加而方向不变。由于静摩擦力具有上述属性,因此其大小一般需要由动力学方程求解得到。

在静摩擦力随外力增加而增加的过程中,静摩擦力有一临界值,当外力沿接触面的分力大小超过此临界值时,物体将开始滑动。这一临界值称为最大静摩擦力。实验证明,最大静摩擦力与物体间的正压力成正比,以 $F_{lamax}$ 表示最大静摩擦力,以 $F_{N}$ 表示物体间的正压力,则

$$F_{\text{fsmax}} = \mu_{\text{s}} F_{\text{N}} \tag{1.2.6}$$

式中,比例系数 $\mu_s$ 称为静摩擦因数,它取决于接触面的材料与接触面的表面状态等。一般情况下,静摩擦力 $F_{ts}$ 满足关系: $F_{ts} \leq F_{tsmax}$ 。

当人推木箱的力增加到一定程度,即其水平分力超过最大静摩擦力时,木箱开始滑动,这时的摩擦力即为滑动摩擦力。物体所受滑动摩擦力的方向总是与物体运动方向相反。实验证明,滑动摩擦力的大小与物体接触面上的正压力成正比,以 F_a表示滑

动摩擦力,则

$$F_{\alpha} = \mu_{k} F_{N} \tag{1.2.7}$$

式中,比例系数 $\mu_k$ 称为动摩擦因数,它取决于接触面的材料与接触面的表面状态,进一步讲,还与相对滑动速度有关。一般物理手册和资料中给出的摩擦因数都是指在一定速度范围内的平均值。表 1-1 列出了一些材料在干燥条件下的摩擦因数值供参考。

上面物体与下面物体	静摩擦因数 $\mu$ ,	动摩擦因数 $\mu$
钢铁与钢铁	0.70	0.50
铝与钢铁	0.61	0.47
铜与钢铁	0.53	0.36
锌与铸铁	0.85	0.21
铜与玻璃	0.68	0.53

表 1-1 一些材料在干燥条件下的静崖榕因数与动魔榕因数

在物体之间相对速度不太大时,动摩擦因数 $\mu_{k}$ 要比静摩擦因数 $\mu_{k}$ ,小一些。但在进行一般计算时,常可认为二者近似相等,即 $\mu_{k} \approx \mu_{s}$ 。

1.2.3 牛顿运动定律的应用

质点动力学的典型问题大体可以分成两类,这两类问题与质点运动学的两类问题相对应,且是它们的延伸。第一类问题是已知质点的运动,求作用在质点上的力。具体做法就是先由运动方程通过求导数依次求出速度及加速度,然后借助牛顿第二定律求出力。第二类问题是已知作用在质点上的力,求质点的运动情况。这类问题又可细分为恒力和变力两种情况,前者对应的加速度是恒定值,后者对应的加速度是变化量。显然,前者是后者的特例。

应用牛顿运动定律解题大体步骤如下:

• (1)根据问题要求,确定研究对象,采用隔离体法分析所研究物体的受力情况。所谓隔离体法,就是将所研究物体和周围物体隔离开来,将周围物体作用于所研究物体的力找出来,并画出受力图。
  • (2) 分析物体的运动情况,选择建立恰当的坐标系。
• (3) 依据坐标轴的指向,将物体所受力向各坐标轴投影,求出各力沿坐标轴的分量,写出牛顿第二定律沿各坐标轴的分量式。
  • (4) 求解代数或微分方程,并对结果加以必要的讨论。 在解题中应当养成先用代数符号进行演算的习惯。先用代

数符号进行演算,得出结果的表达式后,再以具体数值代入计算得出最终结果。这样做,便于核对、检查演算过程中是否有错误,而且如果某些量在计算过程中消去了,还可减轻数值计算的工作量。当需讨论数值变化对结果的影响时,也不必重新演算,只需在结果表达式中代值计算、讨论即可。

下面通过具体例子说明解题的步骤与方法。

例题 1-9

升降机内有一倾角为 $\theta$ 的光滑斜面,斜面上有一质量为m的物体,求当升降机以加速度 $a_1$ 上升时,物体相对于斜面和相对于地面的加速度。

解:设物体相对于斜面和相对于地面的加速

度分別 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4,

$$\begin{cases} a_x = a_{rx} = a_r \cos \theta \\ a_y = a_1 - a_{ry} = a_1 - a_r \sin \theta \end{cases}$$

将物体 m 单独隔离出来,物体 m 受力有两个,一个是重力 mg,竖直向下;另一个是斜面对物体的弹力 $F_N$ ,垂直斜面指向右上方。由牛顿第二定律,得

$$\begin{cases} F_{N} \sin \theta = ma_{x} \\ F_{N} \cos \theta - mg = ma_{x} \end{cases}$$

将前面 $a_x$ 、 $a_y$ 关系式代入上式,得 $a_r = (g + a_1) \sin \theta$ ,方向沿斜面向下;将其代回前式,得

$$\begin{cases} a_x = (g+a_1)\sin \theta\cos \theta \\ a_y = a_1\cos^2\theta - g\sin^2\theta \end{cases}$$

相对地面的加速度 $\mathbf{a} = a_{\mathbf{z}} \mathbf{i} + a_{\mathbf{y}} \mathbf{j}$ 。

例题 1-10

如图 1-15 所示,一个质量为 m 的小球系在绳的一端,绳的另一端固定在天花板上的 O 点,绳长为 l。先拉动小球使绳保持水平静止,然后松手使小球下落。求:绳下摆至 $\theta_0$ 角时,小球的速率和绳中的张力。

解:小球做变速圆周运动。小球受两个力,一个是重力 mg,竖直向下;另一个是绳子张力 $F_{\tau}$ ,方向沿绳子指向圆心 O。

图 1-15 摆球的运动

选用自然坐标系,小球在任意 t 时刻摆至 $\theta$ 角时,牛顿第二定律的切向分量式为

$$mg\cos\theta = ma_t = m\frac{\mathrm{d}v}{\mathrm{d}t}$$

积分此式即可得出速率 v 与角度 $\theta$ 的关系,但由于此式中还含有时间 t,应先设法消去,为此作代换 $\frac{dv}{dt} = \frac{dv}{ds} \frac{ds}{dt} = v \frac{dv}{ds}$ ,而 $ds = ld\theta$ ,代

人上式,分离变量,得到

$$gl\cos\theta d\theta = vdv$$

由初始条件:t=0 时, $\theta=0$ 、v=0;设角度为 $\theta$ 时,速率为 v;将上式两边同时积分,有

$$\int_0^\theta g l \cos \theta d\theta = \int_0^v v dv$$

得到 $v = \sqrt{2gl\sin\theta}$ 。当摆至 $\theta_0$ 角时,小球的 速率为 $v(\theta_0) = \sqrt{2gl\sin\theta_0}$ 。

当绳下摆至任意 $\theta$ 角时,牛顿第二定律的法向分量式为

$$F_{\rm T}$$

-mgsin $\theta = ma_n = m \frac{v^2}{l}$

将 $v = \sqrt{2g l \sin \theta}$ 代人,解得 $F_{\tau} = 3mg \sin \theta$ 。 当摆至 $\theta_0$ 角时,绳中的张力为 $F_{\tau}(\theta_0) = 3mg \sin \theta_0$ 。

1.2.4 力学相对性原理与非惯性系

通过前面讨论我们已经知道,适用于牛顿运动定律的参考系称为惯性系。那么惯性系有哪些呢?非惯性系中的问题又应如何处理呢?本节就来讨论这些问题。

1. 力学相对性原理

在相对运动一节中,我们将质点相对于静止参考系的加速度记为a,称为绝对加速度;质点相对于运动参考系的加速度记为a',称为相对加速度;运动参考系相对静止参考系的加速度记为 $a_0$ ,称为牵连加速度。三者之间满足关系 $a=a_0+a'$ ,此即式(1.1.40)。这个结论导出的前提,是假定两个坐标系相应的坐标轴在运动中保持彼此平行,这种情况称为平动。现在将地球作为静止参考系,由于地球是满足一定精度的惯性系,适用牛顿第二定律.因此有

$$F = ma \tag{1.2.8}$$

将a的表达式代入,得

$$\mathbf{F} = m\mathbf{a}_0 + m\mathbf{a}' \tag{1.2.9}$$

这里应区分牵连加速度 $a_0 = 0$ 和 $a_0 \neq 0$ 两种情况,分别加以讨论。 当牵连加速度 $a_0 = 0$ 时,意味着运动参考系相对地球静止参 考系的速度 $v_0$ 等于常矢量,运动状态为匀速直线运动。这时绝 对加速度与相对加速度相等,即a = a',式(1.2.9)变为

$$\boldsymbol{F} = m\boldsymbol{a}' \tag{1.2.10}$$

这就是说,在相对地球静止参考系这一惯性系做匀速直线运动的参考系中,牛顿运动定律仍然成立,所以这种参考系也是惯性系。推而广之,所有相对于惯性系做匀速直线运动的参考系都是惯性系。由于相对于惯性系做匀速直线运动的速度 $v_0$ 可取任意定值,因此惯性系的数量是无穷多的。

在相互做匀速直线运动的参考系中,牛顿运动定律均成立,换句话说,就是相互做匀速直线运动的参考系都是等价的,它们中的任何一个参考系都可以被认为是静止的,"静止"并无绝对意义。伽利略曾在一艘做匀速直线运动的大船的密闭船舱中对大量现象进行了观察研究,他将结果概括如下:一个相对于惯性系做匀速直线运动的参考系,其内部所发生的一切力学过程,都不受系统作为整体的匀速直线运动的影响。或者说,不可能在惯性系内借助于任何力学实验来确定该惯性系本身是处于静止状态,还是处于匀速直线运动状态。这条原理称为力学相对性原理或伽利略相对性原理。

2. 加速平动参考系中的惯性力

当牵连加速度 $a_0 \neq 0$ 时,意味着运动参考系相对地球静止参考系做加速运动,由式 (1.2.9) 可知,物体所受的合外力将不再等于物体的质量乘上物体相对该坐标系的加速度,即 $F \neq ma'$ ,牛顿运动定律相对于此类参考系不再成立。这一结论是普遍适用的,即只要运动参考系相对于惯性系有加速度,不论是加速平动还是转动,该运动参考系就是非惯性系,牛顿运动定律都不再成立。

下面,先来讨论加速平动参考系中的问题。为此,将式(1.2.9)改写为

$$\mathbf{F} - m\mathbf{a}_0 = m\mathbf{a}' \tag{1.2.11}$$

如果将这里的-ma。也理解为质点所受到的一个力,则式 (1.2.11)形式上仍然是牛顿运动定律,可按前面所述的处理牛顿运动定律的方法正常求解。这里的-ma。称为惯性力,记为

$$\boldsymbol{F}_{HR} = -m\boldsymbol{a}_0 \tag{1.2.12}$$

这样,我们将力的概念进行了扩充,除了来自于物体之间相互作用的牛顿力之外,还有一种并非来自于物体之间的相互作用,仅仅是由于坐标系之间的加速运动,为了处理问题方便而人为引入的惯性力。由此可见,惯性力只有受力者没有施力者,因而也就没有反作用力。对于加速平动的参考系来说,惯性力的大小等于物体的质量乘以参考系本身相对惯性系的加速度,惯性力的方向与参考系相对惯性系的加速度方向相反。这种情况与地球的重力场相类似,物体所受重力的大小等于物体的质量乘以重

力加速度,重力的方向与重力加速度方向一致。相对于加速平动参考系出现了惯性力,正好像是出现了某种"重力场"。这一现象对于广义相对论的建立曾给予很大的启发。

惯性力在日常生活中很常见,例如大街上匀速行驶的公交车,当遇到紧急情况而急刹车时,汽车相对地面惯性系的加速度指向车的后方,以汽车为参考系,乘客虽未受到牛顿力作用,但却受到向前的惯性力作用因而向前倾倒。在地面上的行人看来,乘客的向前倾倒完全是惯性的作用。非惯性系中的惯性力从惯性系来看不过是惯性的表现而已。

例题 1-11

如图 1-16 所示,在倾角为 θ 的光滑斜面上有一质量为 m 的物体,平行于斜面的细绳一端连接物体,另一端固定于斜面顶部。若斜面相对地面向左方做加速运动,问:当物体 刚开始脱离斜面时,斜面加速度的大小 α。应等于多少?

$a_0$ $F_T$ m $ma_0$ mg $\theta$

图 1-16 物体受惯性力

解:物体 m 没有脱离斜面时,所受牛顿力有三个:重力 mg 竖直向下,绳子拉力 $F_T$ 沿斜面向左上,斜面支持力 $F_N$ 垂直斜面向右上。由于斜面对地有加速度 $a_0$ ,如以斜面为参考系,则物体还受一惯性力,惯性力大小为 $ma_0$ ,方向水平向右。物体相对斜面静止,

四力平衡。垂直斜面方向有 $F_N + ma_0 \sin \theta = mg \cos \theta$ 。当斜面加速度 $a_0$ 足够大,物体刚开始脱离斜面时,有 $F_N = 0$ ,于是有 $a_0 = g \cot \theta$ 。

3. 匀速转动参考系中的惯性离心力

当我们观察汽车转弯时会看到,坐在车上的人会向弯道的外侧倾斜。如以汽车为参考系,乘客并未受到横向推力,但却向外倾斜,可见在有转动的参考系中,牛顿运动定律不再成立。转动参考系也是非惯性系。

我们来讨论一个以匀角速度 ω 绕竖直轴转动的圆盘,盘上沿半径方向有一直槽。将一质量为 m 的小滑块置于槽内,并通过一根轻弹簧与圆盘的中心轴相连。设直槽与小滑块之间光滑无摩擦。当圆盘转动时,小滑块将随之一起转动,如图 1-17 所示。

以地面为参考系,小滑块相对地面做圆周运动,沿半径方向 受到弹簧拉力 F 的作用,弹簧拉力提供向心力,满足

$$F = ma_n = -m \frac{v^2}{r}e_r = -m\omega^2 re_r$$

式中,e, 是径向单位矢量,方向沿半径向外。向心加速度 a, 的方

图 1-17 转动参考系

向与 e. 的方向相反。

再以圆盘为参考系,小滑块相对圆盘是静止的,虽然它受到 弹簧力却并没有向转轴的方向运动,所以牛顿运动定律不再适 用。如果希望仍能沿用牛顿运动定律,则须引入一个假想的力, 这个力与弹簧力平衡,使得小滑块静止。显然,这个力的大小应 等于小滑块做圆周运动的向心力,而方向与其相反,即沿半径向 外,记为

$$F_{\text{m}} = -ma_{\text{n}} = m\frac{v^2}{r}e_{r} = m\omega^2 re_{r} \tag{1.2.13}$$

这个力是物体惯性在转动参考系中起作用的结果,属于惯性力,且因其方向背离圆心向外,故称惯性离心力。应该注意:对于惯性离心力同样找不到施力者,也没有相应的反作用力。在这里由于惯性离心力和在惯性系中观察到的向心力大小相等、方向相反,所以容易被误解为两者是作用力和反作用力。实际上惯性离心力与向心力(弹簧的拉力)都是作用在小滑块上的,这与作用力和反作用力分别作用在两个物体上的情况截然不同。向心力的反作用力是小滑块作用于弹簧上的力,通常称为离心力,属于牛顿力。

前面已经述及,我们在讨论一般力学问题时,可将地球作为惯性系。但由于地球存在自转和公转,相对太阳有加速度,严格说来属于非惯性系。只是由于地球转动的影响较小,一般可将其作为近似程度较高的惯性系看待而已。尽管地球转动的影响较小,但是在一些问题上还是有所表现。例如,正是由于地球的自转,使得物体所受重力不等于万有引力,重力加速度随地球纬度不同而不同。

例题 1-12

试分析地球上物体的表观重力与纬度的关系。

解:如图 1-18 所示,这里只考虑地球自转的影响。

设在地球表面纬度为 $\theta$ 处,我们用一弹簧秤称量物体m的重量。物体m所受力有三个:一是万有引力F,方向指向地心O;二是弹簧拉力 $F_{T}$ ,方向背离地心但有一很小的偏斜角(图中所画是有意夸大了的);三是惯性离心力 $F_{m}$ ,方向垂直地球转轴向外。

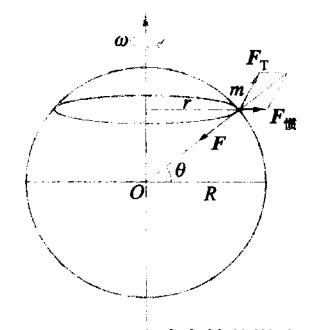
图 1-18 地球自转的影响

三个力平衡,物体处于静止状态,即 $F+F_{r}+F_{rr}=0$

从这里可以看出,万有引力与惯性离心力的方向都是确定的,弹簧拉力的方向只有背离地心并有一偏斜角时,才能保证物体受力平衡。

设地球自转角速度为 ω, 地球半径为 R, 物体 m 做圆周运动的速率为 $v = ωr = ωR\cos θ$ , 惯性离心力大小为

$$F_{\text{th}} = m \frac{v^2}{r} = m\omega^2 R \cos \theta$$

表观重力等于弹簧秤示数,方向与弹簧拉力 $F_{\rm T}$ 相反,记为

$$W = -F_{T} = F + F_{H}$$

由余弦定理,表观重力的大小为

$$W = F_T = \sqrt{F^2 + F_{ex}^2 - 2F \cdot F_{ex}} \cos \theta$$

以 g 表示表观重力加速度, $g_0$ 表示万有引力加速度,即 W=mg, $F=mg_0=m\frac{Gm'}{R^2}$ ,则有

$mg = \sqrt{(mg_0)^2 + (m\omega^2R\cos\theta)^2 - 2m^2g_0\omega^2R\cos^2\theta}$ 因 $\omega^4$ 很小,故根号中第二项可以忽略,再对剩余两项作级数展开,有

$$mg \approx mg_0 \sqrt{1 - \frac{2\omega^2 R \cos^2 \theta}{g_0}}$$ $$\approx mg_0 \left(1 - \frac{\omega^2 R \cos^2 \theta}{g_0}\right)$$

在地球两极处,纬度 $\theta$ =90°, cos $\theta$ =0,g=g0, 此时惯性离心力为零,重力加速度等于万有引力加速度,即表观重力等于万有引力,表观重力为最大值;在地球赤道上,纬度 $\theta$ =0, cos $\theta$ =1,g 最小,此时惯性离心力最大,表观重力等于万有引力与惯性离心力之差(三者共线),表观重力为最小值。从极地到赤道,随着纬度的降低,重力加速度 g 逐渐减小,表观重力亦逐渐减小。

*4. 科里奥利力

一般来讲,物体在转动参考系中不一定是静止的。现在就来讨论在匀速转动参考系中,物体有相对运动的情况,这时除了要考虑惯性离心力之外,还要考虑另一种惯性力——科里奥利力。

如图 1-19 所示。有一圆盘以匀角速度 $\omega$ 绕竖直轴转动,质量为 m 的质点被一长为 r 的轻绳连接到圆心 O 点,设质点与圆盘之间光滑无摩擦。现在,令质点在圆盘上做匀速率圆周运动,即质点相对圆盘的速度 v'的大小保持恒定,方向与圆盘转动方向一致。考察质点运动的受力情况。

根据相对运动的速度变换关系式(1.1.39),质点相对地面的速率为 $v=v'+\omega r$ ,以地面为参考系,质点受绳子的拉力 F 做匀速率圆周运动,沿法向有下列关系成立:

$$F = m \frac{v^2}{r} = m \frac{(v' + \omega r)^2}{r} = m \frac{{v'}^2}{r} + 2mv'\omega + m\omega^2 r$$

将等式右边第二、第三项移到左边,有

$$F-2mv'\omega-m\omega^2r=m\frac{{v'}^2}{r}$$

图 1 19 科里奥利力

等式左边第一项 F 是绳子的拉力,属于牛顿力;左边第三项- $m\omega^2 r$ 就是前面提到的惯性离心力,因为沿圆运动的法向是指向圆心的,这里的负号表示方向背离圆心。左边第二项又是一种惯性力,称为科里奥利力,从中可以看出,科里奥利力的大小与物体本身的质量 m 有关,与转盘的角速度 $\omega$ 有关,与质点相对于转盘的速率 v' 有关。式中的负号同样表示本例中科里奥利力的方向也是背离圆心的。上式表明,在考虑了绳子施与质点的牛顿力和两种惯性力之后,在匀速率转动非惯性系中,牛顿运动定律形式上仍然成立。

根据理论力学理论,一般形式的科里奥利力 $F_c$ 的矢量表达式为

$$\boldsymbol{F}_{c} = -2m\boldsymbol{\omega} \times \boldsymbol{v}' \tag{1.2.14}$$

式中,v'是物体 m 相对转动参考系的速度, $\omega$ 是转动参考系的转动角速度。角速度一般情况下定义为矢量,它的大小即为 $\omega$ ,它的方向与转轴平行,其指向与转动方向之间的关系符合右手螺旋定则。如图 1-20 所示,右手握住转轴使四指沿转动方向弯曲,拇指方向即为角速度的方向。式中 $\omega \times v'$ 称为 $\omega$ 与 v' 的矢量积,也称叉积,其结果仍为矢量。它的大小等于 $\omega v'$ sin $\theta$ , $\theta$ 是 $\omega$ 与 v' 之间的夹角,方向按右手螺旋定则确定:先将右手四指并拢指向 $\omega$ 方向,再弯曲四指转向 v' 的方向,则右手拇指的指向即为 $\omega \times v'$ 的方向。式(1.2.14)中的负号表示 $F_c$ 与 $\omega \times v'$ 的方向相反。由此可见,一般情况下的科里奥利力,除了上面提及的与 m、 $\omega$ 、v' 有关外,还与 $\omega$ 与 v' 的夹角有关。前面图 1-19 所示的质点在圆盘上做圆周运动的例子中, $\omega$ 的方向垂直圆盘面向上,v' 的方向在圆盘面内,两者方向相互垂直, $\omega$ 与 v' 的夹角正弦等于 1,所以没有出现在算式中。 $\omega \times v'$ 的方向指向圆心,前面的负号则表示 $F_c$ 的方向背离圆心向外。

人类居住的地球可视为匀角速度转动的非惯性系,除了受到前面提及的惯性离心力影响以外,当物体相对地球运动时,还要受到科里奥利力的作用。运动物体受科里奥利力的影响尽管很小,但还是在许多方面有所表现。根据式(1.2.14),在北半球运动物体所受科里奥利力的方向(或其在地面的投影方向)指向物体运动方向的右侧,而在南半球刚好相反。人们已观察到了一些现象,例如,北半球的河流右岸冲刷严重,单向行车的铁轨右侧磨损较甚,从卫星上观察流向低压中心的气流呈逆时针旋转等。还有科技馆中的傅科摆,它是利用单摆摆面的旋转证实地球自转的著名实验。再有落体偏东现象,高空自由下落的物体落点相比垂足向东偏移,偏东的数值,在赤道处最为显著,在两极则为零。这

图 1-20 角速度矢量的方向

些现象均证实了科里奥利力的存在。