研究物体的运动时,对于一个具体问题,需要根据一定的 条件和要求,突出主要因素,忽略次要因素,以便抓住问题的实 质。这里一方面需要把研究对象简化成理想模型,另一方面还 要适当采用一些理想化方法。力学中主要涉及两种理想化模 型:质点和刚体。关于刚体的问题将在下面的章节中予以讨论, 这里先讨论质点。所谓质点,是指具有一定的质量,而无大小和 形状的一个点。有两种情形可以将物体简化为质点:一是物体运 动时,物体上各个点的运动情况完全相同,任意一点的运动都能 代表物体整体的运动;二是物体本身的尺度远小于物体运动的 范围。
1.1.1 参考系与坐标系
1. 参考系
宇宙万物都处于永恒的运动之中,绝对静止的物体是不存在的,这是运动的绝对性。然而物体运动又有其相对性,一个物体的运动总是相对另一物体而言的。为了描述一个物体的运动,必须另选一个物体(或物体系)作为参考,然后研究这一物体相对于被选作参考的物体的运动。这个被选作参考的物像称为参考系。一般来讲,对于同一物体的运动,选择不同的参考系,运动的描述也是不同的。例如,在一条笔直的道路上有一辆匀速行驶的汽车,车上一人向上抛出一个小球。选择汽车作为参考系,小球做竖直上抛运动,运动轨迹是直线;而如选择地面作为参考系,则小球做斜抛运动,运动轨迹是抛物线。
研究物体的运动学问题,参考系的选择是任意的,主要看问题的性质和研究是否方便。必须明确,参考系一经选定,物体运动的描述也就确定。在下面的讨论中,若无特别声明,通常均以地面为参考系。
2. 坐标系
为了定量地描述物体的运动,还需要在参考系上建立一个适当的坐标系,将坐标系的原点和轴线固定在参考系上。坐标系可以有不同的选择,一般有直角坐标系、球坐标系、柱坐标系,还有平面极坐标系、自然坐标系等。对于一个具体问题,选择恰当的坐标系,可以给研究带来方便,否则将使问题变得繁杂。研究者的首要任务就是针对具体要研究的问题,选择一个合适的坐标系。
当我们研究一个物体相对某一坐标系的运动时,参考系常常并不出现,原因是坐标系和参考系是固定在一起的,此时的坐标系实质上充当了参考系的化身,是参考系的几何抽象。
1.1.2 描述质点运动的物理量
描述质点运动的物理量主要有:位置矢量、位移、速度与加速度等。下面首先采用矢量法对上述物理量予以定义,后面一节再将它们落实到不同坐标系中,给出各物理量在不同坐标系中的具体表达式。
1. 位置矢量
如图 1-1 所示,若质点某时刻位于 P 点处,则质点在空间的
图 1-1 质点的位矢
位置可用自坐标原点 O 至 P 点的矢量 r 来表示。矢量 r 称为质点的位置矢量,简称位矢,也称径矢。它的大小为该质点到坐标原点的距离 r ,方向由 O 指向 P 。显然,质点在运动过程中,位矢 r 的大小与方向不断变化,可将位矢 r 随时间的变化关系表示为时间函数的形式:
r = r ( t ) (1.1.1) r = r(t) \tag{1.1.1} r = r ( t ) ( 1.1.1 ) 式(1.1.1)给出了质点在任意时刻t的空间位置,称为质点的运动方程矢量式。
2. 位移
设质点沿图 1-2 所示的曲线轨道运动,时刻 t 质点位于 P 点处,相应位矢为 r 1 r_1 r 1 Δ t \Delta t Δ t r 2 r_2 r 2 Δ t \Delta t Δ t Δ t \Delta t Δ t
Δ r = r 2 − r 1 (1.1.2) \Delta \mathbf{r} = \mathbf{r}_2 - \mathbf{r}_1 \tag{1.1.2} Δ r = r 2 − r 1 ( 1.1.2 ) 显然,位移 Δ r \Delta r Δ r P ∖ Q P \setminus Q P ∖ Q
在国际单位制中,位移的单位为 m(米)。
必须注意,位移与路程是两个不同的物理量。位移是矢量,具有大小和方向,它表示质点在 Δ t \Delta t Δ t Δ r \Delta r Δ r Δ t \Delta t Δ t Δ s \Delta s Δ s Δ r \Delta r Δ r ∣ Δ r ∣ |\Delta r| ∣Δ r ∣ Δ s \Delta s Δ s Δ t \Delta t Δ t lim Δ t → 0 ∣ Δ r ∣ \lim_{\Delta t \to 0} |\Delta r| lim Δ t → 0 ∣Δ r ∣ ∣ Δ r ∣ |\Delta r| ∣Δ r ∣ Δ r \Delta r Δ r ∣ Δ r ∣ = ∣ r 2 − r 1 ∣ |\Delta r| = |r_2 - r_1| ∣Δ r ∣ = ∣ r 2 − r 1 ∣ Δ r = ∣ r 2 ∣ − ∣ r 1 ∣ \Delta r = |r_2| - |r_1| Δ r = ∣ r 2 ∣ − ∣ r 1 ∣
3. 速度
速度是描述质点运动的快慢及方向的物理量。
质点在 Δ t \Delta t Δ t v ‾ \overline{v} v
v ˉ = Δ r Δ t (1.1.3) \bar{v} = \frac{\Delta r}{\Delta t} \tag{1.1.3} v ˉ = Δ t Δ r ( 1.1.3 ) 平均速度是矢量,其方向与 Δ r \Delta r Δ r ∣ v ‾ ∣ = ∣ Δ r Δ t ∣ |\overline{v}| = \left|\frac{\Delta r}{\Delta t}\right| ∣ v ∣ = Δ t Δ r Δ t \Delta t Δ t → \rightarrow →
v = lim Δ t → 0 Δ r Δ t = d r d t (1.1.4) v = \lim_{\Delta t \to 0} \frac{\Delta r}{\Delta t} = \frac{\mathrm{d}r}{\mathrm{d}t} \tag{1.1.4} v = Δ t → 0 lim Δ t Δ r = d t d r ( 1.1.4 )
图 1-2 质点的位移
式中 v 称为质点在 t 时刻的瞬时速度,简称速度,它等于位矢 r 对时间的一阶导数。速度是矢量,其方向是 Δ t → 0 \Delta t \rightarrow 0 Δ t → 0 Δ r \Delta r Δ r Δ r \Delta r Δ r
描述质点运动的快慢,还有一个称为速率的物理量。在 Δ t \Delta t Δ t Δ s \Delta s Δ s Δ t \Delta t Δ t Δ t \Delta t Δ t
v ‾ = Δ s Δ t (1.1.5) \overline{v} = \frac{\Delta s}{\Delta t} \tag{1.1.5} v = Δ t Δ s ( 1.1.5 ) 对比式(1.1.3)和式(1.1.5)可知,平均速度是矢量,而平均速率是标量,由于 Δ s \Delta s Δ s ∣ Δ r ∣ |\Delta r| ∣Δ r ∣
但是,当 Δ t → 0 \Delta t \rightarrow 0 Δ t → 0
v = lim Δ t → 0 Δ s Δ t = d s d t = ∣ d r d t ∣ = ∣ v ∣ (1.1.6) v = \lim_{\Delta t \to 0} \frac{\Delta s}{\Delta t} = \frac{\mathrm{d}s}{\mathrm{d}t} = \left| \frac{\mathrm{d}r}{\mathrm{d}t} \right| = |v|
\tag{1.1.6} v = Δ t → 0 lim Δ t Δ s = d t d s = d t d r = ∣ v ∣ ( 1.1.6 ) 其中用到了前面讨论过的 ds = |dr|以及考虑到 dt 应恒为正值的实际情况。由式(1.1.6)可见,速率是标量,速率等于速度矢量的大小。
在国际单位制中,速度和速率的单位是 m·s-1 (米每秒)。
4. 加速度
加速度是描述质点运动速度变化快慢的物理量。
如图 1-3 所示。设质点在 t 时刻位于 P 点,速度为 v 1 v_1 v 1 Δ t \Delta t Δ t v 2 v_2 v 2 Δ t \Delta t Δ t Δ v = v 2 − v 1 \Delta v = v_2 - v_1 Δ v = v 2 − v 1 Δ t \Delta t Δ t
a ‾ = Δ v Δ t \overline{a} = \frac{\Delta v}{\Delta t} a = Δ t Δ v 当 Δ t → 0 \Delta t \rightarrow 0 Δ t → 0
a = lim Δ t → 0 Δ v Δ t = d v d t = d 2 r d t 2 (1.1.7) \boldsymbol{a} = \lim_{\Delta t \to 0} \frac{\Delta \boldsymbol{v}}{\Delta t} = \frac{\mathrm{d}\boldsymbol{v}}{\mathrm{d}t} = \frac{\mathrm{d}^2 \boldsymbol{r}}{\mathrm{d}t^2}
\tag{1.1.7} a = Δ t → 0 lim Δ t Δ v = d t d v = d t 2 d 2 r ( 1.1.7 ) 可见,质点的加速度等于速度对时间的一阶导数,或等于位矢对时间的二阶导数。
加速度是矢量,其方向是 Δ t → 0 \Delta t \rightarrow 0 Δ t → 0 Δ v \Delta v Δ v Δ v \Delta v Δ v
图 1-3 质点的速度增量
凹侧。
在国际单位制中,加速度的单位是 m·s-2 (米每二次方秒)。
1.1.3 直角坐标系中质点运动的描述
以上我们采用矢量法讨论了描述质点运动的主要物理量,所涉及的位矢、位移、速度与加速度都是矢量。采用矢量法给出的定义公式简洁、概念清晰,有助于对问题实质的思考和解决。但是在具体计算尤其是进行矢量叠加计算时,矢量法有时略显麻烦,而如果将矢量放在坐标系中进行讨论和计算,将会带来很多方便。
下面主要讨论直角坐标系、平面极坐标系和自然坐标系。
直角坐标系是最简单的坐标系。取固定于参考系的一点为原点,通过原点作三根两两正交的直线并规定出每根直线的正方向,分别称之为x,y,z坐标轴。这就组成了直角坐标系。为了与矢量运算的法则相一致,通常采用的直角坐标系是右旋系:先将右手并拢的四指指向x轴,然后弯曲四指转向y轴,则拇指的方向指向z轴的正方向。
1. 位矢与轨道方程
在直角坐标系中,质点 P 的位矢 r(图 1-4)可以表示为
r = x i + y j + z k (1.1.8) \mathbf{r} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k} \tag{1.1.8} r = x i + y j + z k ( 1.1.8 ) 其中的 x,y,z 分别为位矢 r 投影到三个坐标轴上所得的分量,注意三个分量本身带正负号;而 i,j,k 分别为沿 x,y,z 轴的单位矢量。所谓单位矢量是指:其大小(或称为模)等于 1 并具有确定指向的矢量。位矢 r 的大小也就是质点 P 所在位置与 O 点之间的距离表示为
r = ∣ r ∣ = x 2 + y 2 + z 2 (1.1.9) r = |r| = \sqrt{x^2 + y^2 + z^2}
\tag{1.1.9} r = ∣ r ∣ = x 2 + y 2 + z 2 ( 1.1.9 ) 位矢 r 的方向可用三个方向余弦表示为
cos α = x r , cos β = y r , cos γ = z r (1.1.10) \cos \alpha = \frac{x}{r}, \quad \cos \beta = \frac{y}{r}, \quad \cos \gamma = \frac{z}{r}
\tag{1.1.10} cos α = r x , cos β = r y , cos γ = r z ( 1.1.10 ) 其中的 α ∖ β ∖ γ \alpha \setminus \beta \setminus \gamma α ∖ β ∖ γ x ∖ y ∖ z x \setminus y \setminus z x ∖ y ∖ z
cos 2 α + cos 2 β + cos 2 γ = 1 (1.1.11) \cos^2 \alpha + \cos^2 \beta + \cos^2 \gamma = 1
\tag{1.1.11} cos 2 α + cos 2 β + cos 2 γ = 1 ( 1.1.11 ) 所以三个方位角中只有两个是独立的。
质点在运动过程中,位矢 r 随时间变化,x、y、z 三个分量亦随时间变化,可将其表示为时间的函数
图 1-4 直角坐标系中质点的 位矢
{ x = x ( t ) y = y ( t ) z = z ( t ) (1.1.12) \begin{cases} x = x(t) \\ y = y(t) \\ z = z(t) \end{cases}
\tag{1.1.12} ⎩ ⎨ ⎧ x = x ( t ) y = y ( t ) z = z ( t ) ( 1.1.12 ) 式(1.1.12)称为质点的运动方程分量式,它与式(1.1.1)等价。
质点运动时途经的点连接形成的空间曲线称为轨道。将运动方程分量式(1.1.12)中的时间 t 消去,可得到两个关于 x 、y 、z 的函数关系式
{ F ( x , y , z ) = 0 G ( x , y , z ) = 0 (1.1.13) \begin{cases}
F(x,y,z) = 0 \\
G(x,y,z) = 0
\end{cases}
\tag{1.1.13} { F ( x , y , z ) = 0 G ( x , y , z ) = 0 ( 1.1.13 ) 此方程组称为质点运动的轨道方程。
2. 位移
位移 Δ r = r 2 − r 1 \Delta r = r_2 - r_1 Δ r = r 2 − r 1
Δ r = r 2 − r 1 = ( x 2 i + y 2 j + z 2 k ) − ( x 1 i + y 1 j + z 1 k ) = Δ x i + Δ y j + Δ z k (1.1.14) \Delta \boldsymbol{r} = r_2 - r_1 = (x_2 \boldsymbol{i} + y_2 \boldsymbol{j} + z_2 \boldsymbol{k}) - (x_1 \boldsymbol{i} + y_1 \boldsymbol{j} + z_1 \boldsymbol{k}) = \Delta x\,\boldsymbol{i} + \Delta y\,\boldsymbol{j} + \Delta z\,\boldsymbol{k}
\tag{1.1.14} Δ r = r 2 − r 1 = ( x 2 i + y 2 j + z 2 k ) − ( x 1 i + y 1 j + z 1 k ) = Δ x i + Δ y j + Δ z k ( 1.1.14 ) 其中
Δ x = x 2 − x 1 , Δ y = y 2 − y 1 , Δ z = z 2 − z 1 (1.1.15) \Delta x = x_2 - x_1, \quad \Delta y = y_2 - y_1, \quad \Delta z = z_2 - z_1
\tag{1.1.15} Δ x = x 2 − x 1 , Δ y = y 2 − y 1 , Δ z = z 2 − z 1 ( 1.1.15 ) Δ x \Delta x Δ x Δ y \Delta y Δ y Δ z \Delta z Δ z Δ r \Delta r Δ r Δ r \Delta r Δ r
3. 速度
速度在直角坐标系中可以表示为
v = d r d t = d d t ( x i + y j + z k ) = v x i + v y j + v z k (1.1.16) \boldsymbol{v} = \frac{\mathrm{d}\boldsymbol{r}}{\mathrm{d}t} = \frac{\mathrm{d}}{\mathrm{d}t} (x\boldsymbol{i} + y\boldsymbol{j} + z\boldsymbol{k}) = v_x \boldsymbol{i} + v_y \boldsymbol{j} + v_z \boldsymbol{k}
\tag{1.1.16} v = d t d r = d t d ( x i + y j + z k ) = v x i + v y j + v z k ( 1.1.16 ) 式中
v x = d x d t , v y = d y d t , v z = d z d t (1.1.17) v_x = \frac{\mathrm{d}x}{\mathrm{d}t}, \quad v_y = \frac{\mathrm{d}y}{\mathrm{d}t}, \quad v_z = \frac{\mathrm{d}z}{\mathrm{d}t}
\tag{1.1.17} v x = d t d x , v y = d t d y , v z = d t d z ( 1.1.17 ) 式中 v x , v y , v z v_x, v_y, v_z v x , v y , v z
v = ∣ v ∣ = v x 2 + v y 2 + v z 2 (1.1.18) v = |v| = \sqrt{v_x^2 + v_y^2 + v_z^2}
\tag{1.1.18} v = ∣ v ∣ = v x 2 + v y 2 + v z 2 ( 1.1.18 ) 如果写成 v = d r d t v = \frac{dr}{dt} v = d t d r d r d t \frac{dr}{dt} d t d r
化率,
d r d t = d ∣ r ∣ d t ≠ ∣ d r d t ∣ \frac{dr}{dt} = \frac{d|r|}{dt} \neq \left| \frac{dr}{dt} \right| d t d r = d t d ∣ r ∣ = d t d r , 将式 (1.1.9) 和式 (1.1.16)—式 (1.1.18) 对比便可一目了然。
4. 加速度
加速度在直角坐标系中可以表示为
a = d v d t = d 2 r d t 2 = a x i + a y j + a z k (1.1.19) \boldsymbol{a} = \frac{\mathrm{d}\boldsymbol{v}}{\mathrm{d}t} = \frac{\mathrm{d}^2 \boldsymbol{r}}{\mathrm{d}t^2} = a_x \boldsymbol{i} + a_y \boldsymbol{j} + a_z \boldsymbol{k}
\tag{1.1.19} a = d t d v = d t 2 d 2 r = a x i + a y j + a z k ( 1.1.19 ) 式中
a x = d v x d t = d 2 x d t 2 , a y = d v y d t = d 2 y d t 2 , a z = d v z d t = d 2 z d t 2 (1.1.20) a_x = \frac{dv_x}{dt} = \frac{d^2x}{dt^2}, \quad a_y = \frac{dv_y}{dt} = \frac{d^2y}{dt^2}, \quad a_z = \frac{dv_z}{dt} = \frac{d^2z}{dt^2}
\tag{1.1.20} a x = d t d v x = d t 2 d 2 x , a y = d t d v y = d t 2 d 2 y , a z = d t d v z = d t 2 d 2 z ( 1.1.20 ) a x , a y , a z a_{x}, a_{y}, a_{z} a x , a y , a z
以上讨论了位矢、位移、速度及加速度矢量在直角坐标系中的表达式,从中可以看出,任一曲线运动都可以分解成沿 x、y、z 三个方向各自独立的直线运动的叠加,这就是运动的叠加原理。例如,抛体运动可以看成水平方向的匀速直线运动和竖直方向的匀加速直线运动的叠加。当然,运动的分解方式不是唯一的。同一运动,在不同的坐标系中,可以分解为不同方向运动的叠加。
1.1.4 运动学的两类问题
由以上讨论可知,如果知道了质点的运动方程,也就知道了质点任意时刻所处的位置,通过逐次对时间求导数就可得到质点任意时刻的速度和加速度,从而能够了解质点运动的全部情况。但这只是问题的一个方面,问题的另一方面,是上述问题的反问题,即如何由加速度或速度求解质点的运动方程。下面就来讨论质点运动学中的这两类问题。
已知位置矢量,求速度和加速度
这类问题只需依照上面所列的速度、加速度公式逐次对时间求导数即可得解。
例题 1-1
已知质点做平面运动,位置矢量为 r = 2 cos π 2 t i + 2 sin π 2 t j ( m ) r=2\cos\frac{\pi}{2}ti+2\sin\frac{\pi}{2}tj(m) r = 2 cos 2 π t i + 2 sin 2 π t j ( m )
(1) 轨道方程:
(2) 从 t=1 s 到 t=2 s 之间质点的平均速度与平均速率:
(3) t=1 s 时质点的速度与速率;
(4) t=1 s 时质点的加速度。
解:(1) 质点位置矢量的分量为 x = 2 cos π 2 t x = 2\cos\frac{\pi}{2}t x = 2 cos 2 π t y = 2 sin π 2 t y = 2\sin\frac{\pi}{2}t y = 2 sin 2 π t
轨道方程为 x 2 + y 2 = 2 2 x^2 + y^2 = 2^2 x 2 + y 2 = 2 2
(2) t=1 s 时质点的位矢 r 1 = 2 j r_1=2j r 1 = 2 j
时质点的位矢 r 2 = − 2 i r_2 = -2i r 2 = − 2 i Δ r = r 2 − r 1 = ( − 2 i − 2 j ) \Delta r = r_2 - r_1 = (-2i - 2j) Δ r = r 2 − r 1 = ( − 2 i − 2 j ) Δ t = ( 2 − 1 ) \Delta t = (2 - 1) Δ t = ( 2 − 1 ) v ‾ = Δ r Δ t = ( − 2 i − 2 j ) \overline{v} = \frac{\Delta r}{\Delta t} = (-2i - 2j) v = Δ t Δ r = ( − 2 i − 2 j ) -1 。又由 r 1 r 2 r_1 \ r_2 r 1 r 2 Δ t = 1 \Delta t = 1 Δ t = 1 Δ s = 2 π R / 4 = π \Delta s = 2\pi R/4 = \pi Δ s = 2 π R /4 = π v = Δ s Δ t = π v = \frac{\Delta s}{\Delta t} = \pi v = Δ t Δ s = π -1 。
(3) 速度函数
v = d r d t = − π sin π 2 t i v = \frac{\mathrm{d}r}{\mathrm{d}t} = -\pi \sin \frac{\pi}{2}ti v = d t d r = − π sin 2 π t i π cos π 2 t j ( m ⋅ s − 1 ) , t = 1 s 时质点的速度 \pi\cos\frac{\pi}{2}t\mathbf{j}(\mathbf{m}\cdot\mathbf{s}^{-1}), t = 1 \text{ s 时质点的速度} π cos 2 π t j ( m ⋅ s − 1 ) , t = 1 s 时质点的速度 v 1 = − π i m ⋅ s − 1 , 速 v = ∣ v 1 ∣ = π m ⋅ s − 1 . v_1 = -\pi\mathbf{i} \mathbf{m}\cdot\mathbf{s}^{-1}, \mathbf{速} \mathbf{v} = |v_1| = \pi \mathbf{m}\cdot\mathbf{s}^{-1}. v 1 = − π im ⋅ s − 1 , 速 v = ∣ v 1 ∣ = π m ⋅ s − 1 . ( 4 ) 加速度函数 a = d v d t = − π 2 2 cos π 2 t i − π 2 2 sin π 2 t j , t = 1 s 时质点的加速度为 (4) \text{ 加速度函数 } \mathbf{a} = \frac{d\mathbf{v}}{dt} = -\frac{\pi^2}{2}\cos\frac{\pi}{2}t\mathbf{i} - \frac{\pi^2}{2}\sin\frac{\pi}{2}t\mathbf{j}, t = 1 \text{ s 时质点的加速度为} ( 4 ) 加速度函数 a = d t d v = − 2 π 2 cos 2 π t i − 2 π 2 sin 2 π t j , t = 1 s 时质点的加速度为 a 1 = − π 2 2 j m ⋅ s − 2 \mathbf{a}_1 = -\frac{\pi^2}{2}\mathbf{j} \mathbf{m}\cdot\mathbf{s}^{-2} a 1 = − 2 π 2 jm ⋅ s − 2
例题 1-2
如图 1-5 所示,河中有一条小船,一根绳子一端系于小船,另一端跨过岸边滑轮并由一人以匀速率 v 0 v_0 v 0
解:如图所示建立坐标系,设某时刻小船到岸边的距离为x,绳长为l,则有几何关系 l 2 = h 2 + x 2 l^2=h^2+x^2 l 2 = h 2 + x 2 l d l d t = x d x d t l\frac{\mathrm{d}l}{\mathrm{d}t}=x\frac{\mathrm{d}x}{\mathrm{d}t} l d t d l = x d t d x d l d t = x d l d t = x d l d t \frac{\mathrm{d}l}{\mathrm{d}t}=x\frac{\mathrm{d}l}{\mathrm{d}t}=x\frac{\mathrm{d}l}{\mathrm{d}t} d t d l = x d t d l = x d t d l
v = d x d t = l x d l d t = − l x v 0 = − v 0 1 + h 2 x 2 v = \frac{dx}{dt} = \frac{l}{x} \frac{dl}{dt} = -\frac{l}{x}v_0 = -v_0\sqrt{1 + \frac{h^2}{x^2}} v = d t d x = x l d t d l = − x l v 0 = − v 0 1 + x 2 h 2
图 1-5 河中小船的运动
加速度为
a = d v d t = − v 0 d d t ( l x ) = − v 0 2 h 2 x 3 a = \frac{\mathrm{d}v}{\mathrm{d}t} = -v_0 \frac{\mathrm{d}}{\mathrm{d}t} \left(\frac{l}{x}\right) = -\frac{v_0^2 h^2}{x^3} a = d t d v = − v 0 d t d ( x l ) = − x 3 v 0 2 h 2 可见,当小船趋近岸边时,距离x减小,速度和加速度均增加,小船做变加速运动,其中负号表示v和a均与x轴反向。
2. 已知加速度或速度求位置矢量
这类问题从数学上讲是上一类问题的逆运算,需要采用积分的方法来求解。由于积分运算的特点,求解此类问题还需要知道质点的初始条件,即 t=0 时刻质点的初始速度和初始位置。根据加速度与不同变量之间的关系,这类问题又可细分为三种情况:① a=a(t),② a=a(v),③ a=a(x)。下面以具体的实例来说明各种情况的处理方法。
一质点做平面运动,加速度 a = 4 t i ( m ⋅ s − 2 ) \mathbf{a} = 4t\mathbf{i} (\mathbf{m} \cdot \mathbf{s}^{-2}) a = 4 t i ( m ⋅ s − 2 ) v 0 = 2 i m ⋅ s − 1 \mathbf{v}_0 = 2\mathbf{i} \mathbf{m} \cdot \mathbf{s}^{-1} v 0 = 2 im ⋅ s − 1
解:本题应按 x、y 两个方向,先分别求速度 再求坐标。由于加速度是时间的函数,积分 较简单。
根据题意,x 方向有 d v x d t = a x = 4 t \frac{dv_x}{dt} = a_x = 4t d t d v x = a x = 4 t d v x = 4 t d t dv_x = 4tdt d v x = 4 t d t v x = 0 v_x = 0 v x = 0 v x v_x v x ∫ 0 t x d v x = ∫ 0 t 4 t d t \int_0^{t_x} dv_x = \int_0^t 4tdt ∫ 0 t x d v x = ∫ 0 t 4 t d t v x = 2 t 2 = d x d t v_x = 2t^2 = \frac{dx}{dt} v x = 2 t 2 = d t d x d x = 2 t 2 d t dx = 2t^2dt d x = 2 t 2 d t ∫ 0 x d x = ∫ 0 t 2 t 2 d t \int_0^x dx = \int_0^t 2t^2dt ∫ 0 x d x = ∫ 0 t 2 t 2 d t x = 2 3 t 3 x = \frac{2}{3}t^3 x = 3 2 t 3
y 方向有 d v y d t = a y = 0 \frac{\mathrm{d}v_y}{\mathrm{d}t} = a_y = 0 d t d v y = a y = 0 v y = 常量 v_y = 常量 v y = 常量 -1 ,所以有 v y = 2 v_y = 2 v y = 2 -1 = d y d t \frac{\mathrm{d}y}{\mathrm{d}t} d t d y d y = 2 d t \mathrm{d}y = 2\mathrm{d}t d y = 2 d t ∫ 0 y d y = ∫ 0 t 2 d t \int_0^y \mathrm{d}y = \int_0^t 2\mathrm{d}t ∫ 0 y d y = ∫ 0 t 2 d t
合并以上结果,得质点的位置矢量为 r = x i + y j = 2 3 t 3 i + 2 t j ( m ) r=x i+y j=\frac{2}{3}t^3 i+2t j(m) r = x i + y j = 3 2 t 3 i + 2 t j ( m )
例题 1-4
质量为 m 的摩托艇在水面上以速度 v 0 v_0 v 0 a = − k m v a=-\frac{k}{m}v a = − m k v
解:(1) 取摩托艇前进方向为 x 轴正向,由题意,有 d v d t = a = − k m v \frac{\mathrm{d}v}{\mathrm{d}t} = a = -\frac{k}{m}v d t d v = a = − m k v d v = a d t \mathrm{d}v = a\mathrm{d}t d v = a d t d v \mathrm{d}v d v d v v = − k m d t \frac{\mathrm{d}v}{v} = -\frac{k}{m}\mathrm{d}t v d v = − m k d t v 0 v_0 v 0
边积分
∫ v 0 v d v v = − ∫ 0 t k m d t \int_{v_0}^v \frac{\mathrm{d}v}{v} = -\int_0^t \frac{k}{m} \mathrm{d}t ∫ v 0 v v d v = − ∫ 0 t m k d t 得 v = v 0 e − k m t v = v_0 e^{-\frac{k}{m}t} v = v 0 e − m k t
(2) 由 v = d x d t = v 0 e − k m t v = \frac{\mathrm{d}x}{\mathrm{d}t} = v_0 e^{-\frac{k}{m}t} v = d t d x = v 0 e − m k t d x = v 0 e − k m t d t \mathrm{d}x = v_0 e^{-\frac{k}{m}t} \mathrm{d}t d x = v 0 e − m k t d t t = 0 t = 0 t = 0 x = 0 x = 0 x = 0 t t t x x x
∫ 0 x d x = ∫ 0 t v 0 e − k m t d t \int_0^x \mathrm{d}x = \int_0^t v_0 e^{-\frac{k}{m}t} \mathrm{d}t ∫ 0 x d x = ∫ 0 t v 0 e − m k t d t 得 x = m k v 0 ( 1 − e − k m t ) x = \frac{m}{k} v_0 \left(1 - e^{-\frac{k}{m}t}\right) x = k m v 0 ( 1 − e − m k t )
例题 1-5
一质点沿 x 轴正向运动,其加速度 a 与坐标 x 之间的关系为 a=x。已知 t=0 时,质点位于 x 0 ( x 0 > 0 ) x_0(x_0>0) x 0 ( x 0 > 0 ) v 0 = 0 v_0=0 v 0 = 0
解:按加速度定义, a = d v d t = x a = \frac{dv}{dt} = x a = d t d v = x a = x = d v d t = d v d x d x d t = a = x = \frac{dv}{dt} = \frac{dv}{dx} \frac{dx}{dt} = a = x = d t d v = d x d v d t d x =
v d v d x v\frac{\mathrm{d}v}{\mathrm{d}x} v d x d v t t t v d v = x d x v\mathrm{d}v=x\mathrm{d}x v d v = x d x ∫ 0 v v d v = ∫ x 0 x x d x \int_{0}^{v} v\mathrm{d}v = \int_{x_{0}}^{x} x\mathrm{d}x ∫ 0 v v d v = ∫ x 0 x x d x v = x 2 − x 0 2 v=\sqrt{x^2-x_{0}^2} v = x 2 − x 0 2
通过以上实例可以看到,如果加速度表达式中含有三个变量,则需要通过变量代换消去其中的一个变量,使得表达式中只含有两个变量;进一步,为了两边同时积分求得速度,需要分离变量,使得等号两边各自只含有一个变量,才能进行积分。这里尤其要注意,不能出现在等式一边含有两个变量的情况下只对其中一个变量积分的错误。至于由速度求坐标,则只会出现表达式中含有两个变量的情况,处理问题的数学方法与上面相同,同样要注意分离变量问题。
1.1.5 平面极坐标系中质点运动的描述
图 1-6 平面极坐标系
在所研究的平面内取固定于参考系的一点为原点 O,极坐标系中称为极点。然后,在该平面内取固定于参考系并由极点向外的一条射线,称为极轴。这就组成了平面极坐标系,如图 1-6 所示。平面上任意一点 P( 不在极点) 的位置,可由两个量来确定:一是 P 点到 O 点的距离 r ,二是 OP 与极轴间的夹角 θ ( \theta( θ ( ( r , θ ) (r,\theta) ( r , θ ) θ \theta θ 0 ≤ θ ≤ 2 π 0 \le \theta \le 2\pi 0 ≤ θ ≤ 2 π e r e_r e r e r e_r e r θ \theta θ e g e_g e g e r e_r e r e g e_g e g e r e_r e r e g e_g e g
1. 位矢
在平面极坐标系中,质点的位矢表示为
r ( t ) = r ( t ) e r (1.1.21) \mathbf{r}(t) = \mathbf{r}(t)\,\mathbf{e}_{r} \tag{1.1.21} r ( t ) = r ( t ) e r ( 1.1.21 ) 式中,r(t)为位矢的大小;位矢的方向与径向单位矢量 e r e_r e r
{ r = r ( t ) θ = θ ( t ) (1.1.22) \begin{cases} r = r(t) \\ \theta = \theta(t) \end{cases}
\tag{1.1.22} { r = r ( t ) θ = θ ( t ) ( 1.1.22 ) 式中,r(t)和 θ ( t ) \theta(t) θ ( t ) θ \theta θ
2. 速度与速率
根据速度定义,将式(1.1.21)对时间求导数,即可得到速度。由于 e, 不是常矢量,根据导数运算法则,求导后速度应分成两项
v = d r d t = d r d t e r + r d e r d t \mathbf{v} = \frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t} = \frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}\mathbf{e}_r + r\frac{\mathrm{d}\mathbf{e}_r}{\mathrm{d}t} v = d t d r = d t d r e r + r d t d e r 参考图 1-7,式中
d e r d t = lim Δ t → 0 Δ e r Δ t = lim Δ t → 0 ∣ e r ∣ Δ θ e θ Δ t = d θ d t e θ \frac{\mathrm{d}\boldsymbol{e}_{r}}{\mathrm{d}t} = \lim_{\Delta t \to 0} \frac{\Delta \boldsymbol{e}_{r}}{\Delta t} = \lim_{\Delta t \to 0} \frac{|\boldsymbol{e}_{r}| \Delta \theta \boldsymbol{e}_{\theta}}{\Delta t} = \frac{\mathrm{d}\theta}{\mathrm{d}t} \boldsymbol{e}_{\theta} d t d e r = Δ t → 0 lim Δ t Δ e r = Δ t → 0 lim Δ t ∣ e r ∣Δ θ e θ = d t d θ e θ 其中用到 ∣ Δ e r ∣ = ∣ e r ∣ Δ θ = Δ θ |\Delta e_r| = |e_r|\Delta \theta = \Delta \theta ∣Δ e r ∣ = ∣ e r ∣Δ θ = Δ θ Δ t → 0 \Delta t \rightarrow 0 Δ t → 0 Δ e r \Delta e_r Δ e r e θ e_\theta e θ
v = d r d t = d r d t e r + r d θ d t e θ = v r e r + v θ e θ (1.1.23) \boldsymbol{v} = \frac{\mathrm{d}\boldsymbol{r}}{\mathrm{d}t} = \frac{\mathrm{d}\boldsymbol{r}}{\mathrm{d}t}\boldsymbol{e}_{r} + r\frac{\mathrm{d}\boldsymbol{\theta}}{\mathrm{d}t}\boldsymbol{e}_{\theta} = v_{r}\boldsymbol{e}_{r} + v_{\theta}\boldsymbol{e}_{\theta}
\tag{1.1.23} v = d t d r = d t d r e r + r d t d θ e θ = v r e r + v θ e θ ( 1.1.23 ) 式中
v r = d r d t , v θ = r d θ d t (1.1.24) v_r = \frac{\mathrm{d}r}{\mathrm{d}t}, \quad v_\theta = r \frac{\mathrm{d}\theta}{\mathrm{d}t}
\tag{1.1.24} v r = d t d r , v θ = r d t d θ ( 1.1.24 ) 是速度 v分别沿径向和横向的分量。v, 称为径向速度,v0 称为横向速度。这里, d θ d t \frac{d\theta}{dt} d t d θ
ω = d θ d t (1.1.25) \omega = \frac{\mathrm{d}\theta}{\mathrm{d}t} \tag{1.1.25} ω = d t d θ ( 1.1.25 ) 在国际单位制中,角速度的单位是 rad·s-1 (弧度每秒)。 质点的速率等于速度的大小,表示为
v = ∣ v ∣ = v c 2 + v θ 2 (1.1.26) v = |\mathbf{v}| = \sqrt{v_{c}^{2} + v_{\theta}^{2}} \tag{1.1.26} v = ∣ v ∣ = v c 2 + v θ 2 ( 1.1.26 ) 作为特例,当质点以极点为圆心,做半径为r的圆周运动时, 其径向速度 v r = d r d t = 0 v_r = \frac{\mathrm{d}r}{\mathrm{d}t} = 0 v r = d t d r = 0 v = d s d t = v θ = r d θ d t = r ω v = \frac{\mathrm{d}s}{\mathrm{d}t} = v_\theta = r \frac{\mathrm{d}\theta}{\mathrm{d}t} = r\omega v = d t d s = v θ = r d t d θ = r ω ω \omega ω
图 1-7 平面极坐标系中单位矢量的变化率
3. 加速度
将式(1.1.23)对时间求导数,可以得到加速度。由于 e r e_r e r e θ e_\theta e θ
a = d v d t = a r e r + a θ e θ (1.1.27) \boldsymbol{a} = \frac{\mathrm{d}\boldsymbol{v}}{\mathrm{d}t} = a_r \boldsymbol{e}_r + a_\theta \boldsymbol{e}_\theta \tag{1.1.27} a = d t d v = a r e r + a θ e θ ( 1.1.27 ) 式中
a r = d 2 r d t 2 − r ( d θ d t ) 2 , a θ = r d 2 θ d t 2 + 2 d r d t d θ d t (1.1.28) a_r = \frac{\mathrm{d}^2 r}{\mathrm{d}t^2} - r \left(\frac{\mathrm{d}\theta}{\mathrm{d}t}\right)^2, \quad
a_\theta = r \frac{\mathrm{d}^2 \theta}{\mathrm{d}t^2} + 2 \frac{\mathrm{d}r}{\mathrm{d}t} \frac{\mathrm{d}\theta}{\mathrm{d}t}
\tag{1.1.28} a r = d t 2 d 2 r − r ( d t d θ ) 2 , a θ = r d t 2 d 2 θ + 2 d t d r d t d θ ( 1.1.28 ) a r a_r a r a θ a_\theta a θ a r a_{r} a r a θ a_{\theta} a θ
d e r d t = d θ d t e θ , d e θ d t = − d θ d t e r (1.1.29) \frac{\mathrm{d}\boldsymbol{e}_{r}}{\mathrm{d}t} = \frac{\mathrm{d}\boldsymbol{\theta}}{\mathrm{d}t}\boldsymbol{e}_{\theta}, \quad \frac{\mathrm{d}\boldsymbol{e}_{\theta}}{\mathrm{d}t} = -\frac{\mathrm{d}\boldsymbol{\theta}}{\mathrm{d}t}\boldsymbol{e}_{r} \tag{1.1.29} d t d e r = d t d θ e θ , d t d e θ = − d t d θ e r ( 1.1.29 ) 在平面极坐标系中,这是两个有用的公式。
例题 1-6
有一圆盘绕通过圆心的竖直轴以匀角速度 ω \omega ω v 0 v_0 v 0
解:选地面为参考系,将圆心0取为极点,运动质点所在半径在t=0时的位置取为极轴。
根据题目所给条件,在任意时刻 t,质点速度的两个分量为
v r = d r d t = v 0 v_r = \frac{\mathrm{d}r}{\mathrm{d}t} = v_0 v r = d t d r = v 0 , v θ = r d θ d t = r ω v_\theta = r \frac{\mathrm{d}\theta}{\mathrm{d}t} = r\omega v θ = r d t d θ = r ω
积分 d r d t = v 0 \frac{\mathrm{d}r}{\mathrm{d}t} = v_0 d t d r = v 0 d θ d t = ω \frac{\mathrm{d}\theta}{\mathrm{d}t} = \omega d t d θ = ω θ = 0 \theta=0 θ = 0
r = v 0 t r = v_0 t r = v 0 t , θ = ω t \theta = \omega t θ = ω t
消去时间 t,得质点运动的轨道方程为 r=
图 1-8 转盘上质点的运动
( v 0 / ω ) (v_0/\omega) ( v 0 / ω ) θ \theta θ
质点加速度的两个分量为
a r = d 2 r d t 2 − r ( d θ d t ) 2 = − r ω 2 a_r = \frac{\mathrm{d}^2 r}{\mathrm{d}t^2} - r \left(\frac{\mathrm{d}\theta}{\mathrm{d}t}\right)^2 = -r\omega^2 a r = d t 2 d 2 r − r ( d t d θ ) 2 = − r ω 2 a θ = r d 2 θ d t 2 + 2 d r d t d θ d t = 2 v 0 ω a_{\theta} = r \frac{\mathrm{d}^2 \theta}{\mathrm{d}t^2} + 2 \frac{\mathrm{d}r}{\mathrm{d}t} \frac{\mathrm{d}\theta}{\mathrm{d}t} = 2v_0 \omega a θ = r d t 2 d 2 θ + 2 d t d r d t d θ = 2 v 0 ω 1.1.6 自然坐标系中质点运动的描述
这里仅限于采用自然坐标系讨论质点的平面运动问题。
在图 1-9 所示的质点运动轨道曲线上取一点 O 为原点,以质点所在的 P 点与原点 O 之间的轨道长度 s 来描述质点的位置,称 s 为质点的自然坐标。在质点所在的 P 点定义两个单位矢量:过 P 点沿轨道的切线方向取单位矢量 e t e_{t} e t e n e_{n} e n e t e_{t} e t e n e_{n} e n e t e_{t} e t e n e_{n} e n
1. 质点的运动方程
当质点运动时,其自然坐标表示为
s = s ( t ) (1.1.30) s = s(t)
\tag{1.1.30} s = s ( t ) ( 1.1.30 ) 此式为自然坐标系中质点的弧线坐标。这样,一个在二维平面内质点的运动,在轨道方程已知的条件下,其运动规律转化为只用一个方程来描述。
2. 速度与速率
在自然坐标系中,质点运动的速度可以用速度的大小即速率 与切向单位矢量的乘积表示为
v = v e t = d s d t e t (1.1.31) \boldsymbol{v} = v\boldsymbol{e}_{t} = \frac{\mathrm{d}s}{\mathrm{d}t}\boldsymbol{e}_{t}
\tag{1.1.31} v = v e t = d t d s e t ( 1.1.31 ) 应当注意,质点在任意点的速度总是沿着轨道的切线方向, 因此,在自然坐标系中质点运动的速度沿单位矢量的投影只有切向分量,没有法向分量。
3. 切向加速度与法向加速度
按加速度定义,将式(1.1.31)对时间求导数即可得到加速度。由于切向单位矢量 e t e_t e t
a = d v d t = d v d t e t + v d e t d t \boldsymbol{a} = \frac{\mathrm{d}\boldsymbol{v}}{\mathrm{d}t} = \frac{\mathrm{d}v}{\mathrm{d}t}\boldsymbol{e}_{t} + \boldsymbol{v} \frac{\mathrm{d}\boldsymbol{e}_{t}}{\mathrm{d}t} a = d t d v = d t d v e t + v d t d e t 如图 1-10 所示,仿照平面极坐标系中求单位矢量变化率的做法,有
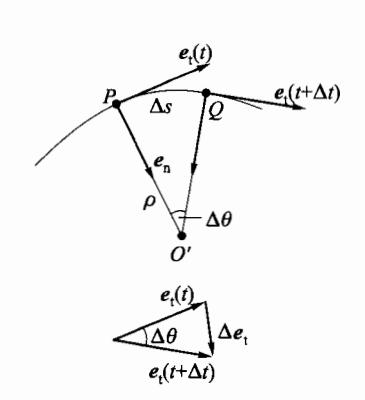
d e t d t = lim Δ t → 0 Δ e t Δ t = lim Δ t → 0 ∣ e t ∣ Δ θ e n Δ t = d θ d t e n \frac{\mathrm{d}\boldsymbol{e}_{t}}{\mathrm{d}t} = \lim_{\Delta t \to 0} \frac{\Delta \boldsymbol{e}_{t}}{\Delta t} = \lim_{\Delta t \to 0} \frac{|\boldsymbol{e}_{t}| \Delta \theta \boldsymbol{e}_{n}}{\Delta t} = \frac{\mathrm{d}\theta}{\mathrm{d}t} \boldsymbol{e}_{n} d t d e t = Δ t → 0 lim Δ t Δ e t = Δ t → 0 lim Δ t ∣ e t ∣Δ θ e n = d t d θ e n 为了求得 d θ / d t d\theta/dt d θ / d t Δ t \Delta t Δ t P ∖ Q P \setminus Q P ∖ Q O ′ O' O ′ ρ \rho ρ e t ( t + Δ t ) e_{t}(t+\Delta t) e t ( t + Δ t ) e t ( t ) e_{t}(t) e t ( t ) P ∖ Q P \setminus Q P ∖ Q Δ θ \Delta \theta Δ θ Δ s \Delta s Δ s P ∖ Q P \setminus Q P ∖ Q
图 1-9 自然坐标系
图 1-10 自然坐标系中单位矢量 的变化率
ρ = lim Δ t → 0 Δ s Δ θ = d s d θ (1.1.32) \rho = \lim_{\Delta t \to 0} \frac{\Delta s}{\Delta \theta} = \frac{\mathrm{d}s}{\mathrm{d}\theta}
\tag{1.1.32} ρ = Δ t → 0 lim Δ θ Δ s = d θ d s ( 1.1.32 ) 这里的 ρ \rho ρ e t e_t e t
d e t d t = d θ d t e n = d θ d s d s d t e n = v ρ e n \frac{\mathrm{d}\boldsymbol{e}_{t}}{\mathrm{d}t} = \frac{\mathrm{d}\boldsymbol{\theta}}{\mathrm{d}t}\boldsymbol{e}_{n} = \frac{\mathrm{d}\boldsymbol{\theta}}{\mathrm{d}s} \frac{\mathrm{d}s}{\mathrm{d}t}\boldsymbol{e}_{n} = \frac{v}{\rho}\boldsymbol{e}_{n} d t d e t = d t d θ e n = d s d θ d t d s e n = ρ v e n 于是得到自然坐标系中加速度的表达式为
a = d v d t = d v d t e t + v 2 ρ e n = a t e t + a n e n (1.1.33) \boldsymbol{a} = \frac{\mathrm{d}\boldsymbol{v}}{\mathrm{d}t} = \frac{\mathrm{d}v}{\mathrm{d}t} \boldsymbol{e}_{t} + \frac{\boldsymbol{v}^{2}}{\rho} \boldsymbol{e}_{n} = a_{t} \boldsymbol{e}_{t} + a_{n} \boldsymbol{e}_{n}
\tag{1.1.33} a = d t d v = d t d v e t + ρ v 2 e n = a t e t + a n e n ( 1.1.33 ) 式中
a t = d v d t = d 2 s d t 2 , a n = v 2 ρ (1.1.34) a_t = \frac{\mathrm{d}v}{\mathrm{d}t} = \frac{\mathrm{d}^2s}{\mathrm{d}t^2}, \quad a_n = \frac{v^2}{\rho}
\tag{1.1.34} a t = d t d v = d t 2 d 2 s , a n = ρ v 2 ( 1.1.34 ) a t , a n a_t, a_n a t , a n a t a_t a t a n a_n a n
a = ∣ a ∣ = a t 2 + a n 2 , tan α = a n a t (1.1.35) a = |\boldsymbol{a}| = \sqrt{a_t^2 + a_n^2}, \quad \tan \alpha = \frac{a_n}{a_t}
\tag{1.1.35} a = ∣ a ∣ = a t 2 + a n 2 , tan α = a t a n ( 1.1.35 ) 式中的 α \alpha α a \boldsymbol{a} a e t \boldsymbol{e}_t e t a n a_n a n a t > 0 a_t>0 a t > 0 α \alpha α a t < 0 a_t<0 a t < 0 α \alpha α
作为曲线运动的特例,如果质点做半径为 r 的圆周运动,则 曲率半径 ρ = r \rho=r ρ = r a n = v 2 / r = r ω 2 a_n=v^2/r=r\omega^2 a n = v 2 / r = r ω 2 v = r ( d θ / d t ) = r ω v=r(d\theta/dt)=r\omega v = r ( d θ / d t ) = r ω a , ≠ 0 a, \neq 0 a , = 0 a n = 0 a_n=0 a n = 0
图 1-11 自然坐标系中加速度的 方向
例题 1-7
列车沿一段圆弧形轨道行驶,自进入圆弧轨道起开始计时,列车的弧线坐标为 s = 30 t − t 3 s = 30t - t^3 s = 30 t − t 3
解:速率 v = d s d t = 30 − 3 t 2 v = \frac{\mathrm{d}s}{\mathrm{d}t} = 30 - 3t^2 v = d t d s = 30 − 3 t 2 a t = d v d t = − 6 t a_t = \frac{\mathrm{d}v}{\mathrm{d}t} = -6t a t = d t d v = − 6 t a n = v 2 r = ( 30 − 3 t 2 ) 2 r a_n = \frac{v^2}{r} = \frac{(30 - 3t^2)^2}{r} a n = r v 2 = r ( 30 − 3 t 2 ) 2 t = 1 s t = 1\text{ s} t = 1 s v = 27 m ⋅ s − 1 v = 27 \text{ m} \cdot \text{s}^{-1} v = 27 m ⋅ s − 1 a t = − 6 m ⋅ s − 2 a_t = -6\text{ m} \cdot \text{s}^{-2} a t = − 6 m ⋅ s − 2 a n = 27 2 500 m ⋅ s − 2 = 1.46 m ⋅ s − 2 a_n = \frac{27^2}{500} \text{ m} \cdot \text{s}^{-2} = 1.46 \text{ m} \cdot \text{s}^{-2} a n = 500 2 7 2 m ⋅ s − 2 = 1.46 m ⋅ s − 2 a = a t 2 + a n 2 = 6.18 m ⋅ s − 2 a = \sqrt{a_t^2 + a_n^2} = 6.18 \text{ m} \cdot \text{s}^{-2} a = a t 2 + a n 2 = 6.18 m ⋅ s − 2 α \alpha α tan α = a n a t = 1.46 − 6 = − 0.2433 \tan \alpha = \frac{a_n}{a_t} = \frac{1.46}{-6} = -0.2433 tan α = a t a n = − 6 1.46 = − 0.2433 α = 166 ∘ 19 ′ \alpha = 166^{\circ}19' α = 16 6 ∘ 1 9 ′ a t < 0 a_t < 0 a t < 0
1.1.7 相对运动
质点运动的描述总是相对于某一参考系而言的,选择不同的参考系就有不同的运动状况,这是运动描述的相对性。例如,在无风的雨天里,雨滴在空中自由下落。站在地面上的人看到的雨滴的运动轨迹是与地面垂直的直线;而坐在行驶的汽车中的人看到的雨滴运动轨迹则是向后倾斜的,车速越快,倾斜角度越大。下面就来研究同一物体相对于两个不同参考系的运动描述之间的关系。
设有两个参考系 K 和 K',在其上建立的直角坐标系分别为 Oxyz 和 O'x'y'z',为简单起见,假定两坐标系相应的坐标轴在运动中保持彼此平行,如图 1-12 所示。这样,K'系相对 K 系的运动,可用坐标原点 O'相对 O 的运动作代表。设有一质点在空间运动,当它位于 P 点时,相对于 O 点的位矢为 r,相对于 O'点的位矢为 r',此时 O'点相对于 O 点的位矢为 r 0 r_0 r 0
r = r 0 + r ′ (1.1.36) \boldsymbol{r} = \boldsymbol{r}_0 + \boldsymbol{r}' \tag{1.1.36} r = r 0 + r ′ ( 1.1.36 ) 此后,经 Δ t \Delta t Δ t O ∖ O ′ O \setminus O' O ∖ O ′ Δ r ∖ Δ r ′ \Delta r \setminus \Delta r' Δ r ∖ Δ r ′ Δ r 0 \Delta r_0 Δ r 0
Δ r = Δ r 0 + Δ r ′ (1.1.37) \Delta \mathbf{r} = \Delta \mathbf{r}_0 + \Delta \mathbf{r}' \tag{1.1.37} Δ r = Δ r 0 + Δ r ′ ( 1.1.37 ) 将式(1.1.36)两边对时间求导数,可得相应速度之间的关系,即
v = v 0 + v ′ (1.1.38) \boldsymbol{v} = \boldsymbol{v}_0 + \boldsymbol{v}' \tag{1.1.38} v = v 0 + v ′ ( 1.1.38 ) 如果 P ∖ K ′ P \setminus K' P ∖ K ′ A ∖ B A \setminus B A ∖ B
v A × C = v A × B + v B × C (1.1.39) \boldsymbol{v}_{A \times C} = \boldsymbol{v}_{A \times B} + \boldsymbol{v}_{B \times C} \tag{1.1.39} v A × C = v A × B + v B × C ( 1.1.39 ) 相应的加速度之间的相对关系为
a A × f C = a A × f B + a B × f C (1.1.40) \boldsymbol{a}_{A \times fC} = \boldsymbol{a}_{A \times fB} + \boldsymbol{a}_{B \times fC} \tag{1.1.40} a A × f C = a A × f B + a B × f C ( 1.1.40 ) 这里关于相对运动的结果是建立在经典时空观基础之上的。 经典时空观与我们的日常生活经验一致,在不同的参考系中时间 是同一个,即时间具有绝对性;另一方面空间也具有绝对性,在不 同的参考系中观察同一个物体,几何尺寸是不变的。绝对时间和 绝对空间的观点是经典力学的基础。在 1905 年,爱因斯坦提出 了狭义相对论,经典时空观得到了改变。这种改变只有在物体的 速度接近真空中光速时才明显,当物体的速度远低于真空光速 时,这里的结果依然正确。
图 1-12 相对运动
例题 1-8
当一客运列车以 22.5 m·s-1 的速率沿水平直线铁轨行驶时,相对地面竖直下落的雨滴在列车车窗上形成的轨迹偏离竖直方向50°,问雨滴相对地面和相对列车的速率分别是多少?
解:参见图 1-13, 雨滴相对地面的速度 v 等于列车速度 v 0 v_0 v 0 v 0 v_0 v 0 v 0 v \frac{v_0}{v} v v 0 v = v 0 tan 50 ∘ v = \frac{v_0}{\tan 50^\circ} v = t a n 5 0 ∘ v 0 -1 ; 而由 v 0 v ′ \frac{v_0}{v'} v ′ v 0
v 0 sin 50 ∘ = 29.4 m ⋅ s − 1 \frac{v_0}{\sin 50^\circ} = 29.4 \text{ m} \cdot \text{s}^{-1} sin 5 0 ∘ v 0 = 29.4 m ⋅ s − 1 。
图 1-13 雨滴的运动