7.6 磁场的能量
在如图 7-15 所示电路中,接通电源后,回路中的电流从零开始达到稳定值 的过程中,电源电动势要克服线圈中的自感电动势 做功,所做的功以能量的形式存贮在自感线
L R
磁场的能量
圈之中。
设在时间 dt 内,电源克服自感电动势所做的功为
在上式中考虑了 和 ,而在回路中电流由 0
到 的整个过程中,电源克服自感电动势所做的总功为
(7.6.1)
这个功就是磁场所贮存的磁能,即
磁能的单位是焦耳(J)。由于载流线圈所贮存的能量绝大多数都集中在线圈所围的磁场之中,所以还可以计算出在磁感应强度为B的磁场中,单位体积中的磁能,即磁能密度 。
设在以上所讨论的回路中,自感线圈是一个长为 l, 匝数为 N, 截面积为 S 的长直螺线管。由例题 7-5 得知它的自感系数 , 而螺线管内的磁感应强度 , 于是式 (7.6.2) 可以写为
式中, 为螺线管所围体积,因此可以得出单位体积中的磁能为
式中, 称为磁能密度,单位为 (焦耳每立方米)。虽然 是从长直螺线管这种特殊情况推导得出,但是可以证明,上式 普遍成立。在已知磁能密度 空间的分布后,通过对遍布磁场的整个空间积分,就可以得出磁场能量,即
(7.6.4)
绷題7 6
求例题 7-4 中的同轴电缆,如图7-16 所示,在通过电流 I 时,长度为 l 的一段中所贮存的磁能。
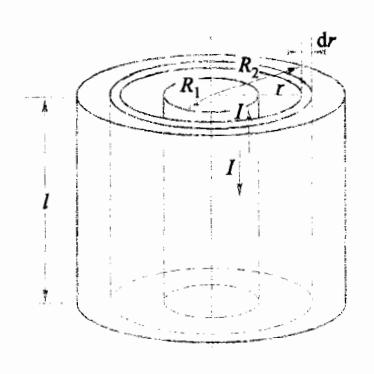
图 7-16 例题 7-6图
解 例题 7-4 已求出同轴电缆中的磁感应强度 ,取一半径为 r、长度为 l、厚度为 dr 的薄圆筒层为体积元,即 ,并且已知磁能仅存在于 区域中,应用式 (7.6.4) 有
思考题与习题
- 7.1 怎样用法拉第电磁感应定律 中的负号确定感应电动势的方向。
- 7.2 在竖直向上的均匀磁场中,水平放置一铜盘,当它绕通过盘心的竖直轴旋转时,转动方向从上往下看是反时针的,在这个铜盘中是否产生感应电动势? 怎样用洛伦兹力说明?
- 7.3 感生电场和静电场有什么相同点和不同点?
- 7.4 把一个白炽灯和一个自感线圈串联后再接上电源,当使用直流电源和交流电源时,电灯的亮度有何不同?设电源的端电压相同。
- 7.5 要设计一个自感系数很大的线圈,应从哪些方面去考虑?
- 7.6 如图所示,一长直导线通以电流 I=10 A,与长直导线共面放置一矩形线圈,线圈 长 l=10 cm,宽a=4 cm,当线圈以 v=10 cm·s-1沿垂直于导线方向运动,求线圈与长直导线相距 d=8 cm 时,线圈中的感应电动势是多少?若线圈平行导线运动,情况又怎样?
题 7.6 图
7.7 一条长为l的导线 A,垂直于一条通过电流为l的 长直导线 B 放置,如图所示,当 其沿平行长直导线以v运动时,求该导线上的动生电动势为多少?并指明哪点电势高(导线 A 左端距导线 B 最近,距 离为d)。
7.8 如图所示,由均匀金属丝折成边长为l的等边三角形,总电阻为R,在磁感应强度为B的均匀磁场中,绕三角形高 ac 为轴以恒定角速度 转动,求线圈平面与B 平行时,金属框的总感应电动势及 ab、ac 间的电势差 、 。
7.9 如图所示,长为 0.5 m 的导体杆在 U 形金属 轨道上无摩擦滑动。当速度为 1 m·s-1时,由于产生感生 电流而受到阻力为 0.8 N,若想使该导体杆以 3 m·s-1 匀速运动,求所需外力要多大?(设回路电阻不变。)
7 10 如图所示,一通以电流 I 的长直导线旁边有一长方形线圈,长为 b,宽为 a,电阻为 R,当线圈绕轴 00′转过 180°时,问线圈中流过的感应电荷量共多少? 设导线与线圈轴的距离为 d。
题 7.10图
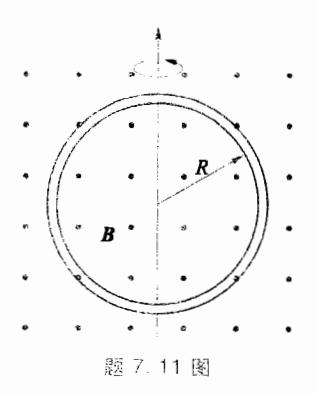
如图所示,半径 R=10 cm 的圆形线圈共绕 N=50 匝,在 B=0.2 Wb·m-2 的均匀磁场中匀速转动,转速为每秒 10 转,转轴垂直于磁场,试求线圈中的最大感应电动势。
如图所示,长为 20 cm、截面为 、绕有线圈 匝的长直螺线管,其内充满相对磁导率 的铁芯,将它经过反向开关 S 与电源相连接,使螺线管中通过 A 的电流,在此螺线管的中部外套有一个 匝的线圈,与电流计 G 相连,
问:若扳动开关使 线圈内电流反向,此过程用时为 0.02 s,则 线圈中的感生电动势是多大?
/ 13 如图所示,在 ,=700、截面面积 S=2 cm²、周长 =35 cm 的铁环上,绕有 =500 匝的线圈构成螺绕环,螺绕环经过反向开关 S 与电源相连,使其通过电流 =0.6 A。在螺绕环外套有一个 =5 匝的线圈,与电流计 G 相连,此回路总电阻 R=800 ,试问:若在 0.05 s 内扳动开关 S,使螺绕环中电流反向,则电流计 G 中通过的电流为多少?
题 7.13图
- 14 如图所示,在一个限定于圆柱形体积内的 均匀磁场,磁感应强度为 B,圆柱的半径为 R,B 的数 值以 T·s-1恒定速率减小,当把电子放在磁场中 a、b、c 各点处时,试求电子所获得的瞬时加速度(数值与方向)各为多少(假定 r=5.0 cm)?
题 7.14 图
7.15 如图所示,在半径为 R 的圆柱体积内存在 匀强磁场 B, 有一长为 l 的金属杆放在磁场里, 圆心距 杆为 b。设 B 以速率 变化,试证:杆上感应电动势的 大小为 。
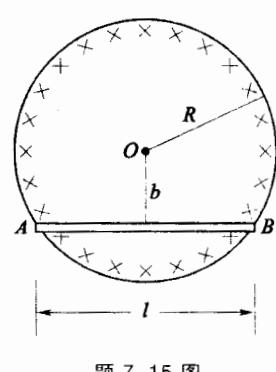
题 7.15图
7.16 如图所示,求半径为 a、线心相距为 d 的平 行输电线单位长度的自感系数。(设导线内部的磁通 量忽略不计。)
题 7.16图
- *7.17 求同轴电缴单位长度上的自感系数。设同 轴电缆芯的半径为 R., 外层导体筒的半径为 R., 两者 间介质的相对磁导率为 ,芯的磁导率为 。
- 7.18 如题 7.6图所示,在一通有电流 / 的直导 线附近,放置一个与直导线共面的矩形线圈,线圈长 l、宽 a, 求直导线与矩形线圈间的互感系数。
- 7.19 如图所示,为一横截面是矩形的螺绕环, 环的内、外半径分别为 、 , 环厚为 a, 其上密绕 N
而导线, 求其电感系数。若在线圈外再绕 N. 而线圈, 求两个线圈的互感系数。若在N、匝的线圈中通以电 流 . 则断开的 N 匝线圈的感生电动势是多 少?(其中 iα、ωα 是常量。)
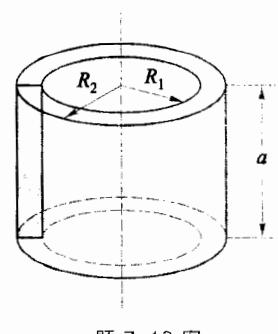
题 7.19 图
- 7.20 在环状铁芯上绕有 N=1 000 匝线圈,设环 的平均半径为 R=8 cm,环的截面积 S=1 cm2,铁芯的 , 问:
- (1) 螺绕环的自感系数是多少?
- (2) 若线圈中通以电流 I=1 A,其中磁场能量及 磁能密度各等于多少?
- 7.21 如图所示, 一长 直螺线管长 l=100 cm, 截 面积 S=1 cm2,线圈的匝数 000 匝,在其中央部 分绕有一副线圈 匝,管内介质 。电路 1 中通以交变电流 , 其中 A, f =50 Hz。求:
- (1) 1、2 两线圈间的互感系数;
- (2) 副线圈 2 中的感生电动势(提示: B=
题 7.21图