7.5 自感与互感

7.5.1 自感现象与自感系数

实验证明,当一个线圈中的电流发生变化时,线圈本身会因此产生感生电动势,这种现象叫自感现象,由此而产生的感生电动势称为自感电动势,用 $\mathcal{E}_{L}$ 表示。

根据法拉第电磁感应定律,可以得出任意形状的线圈产生的 自感电动势为

$$\mathscr{E}_L = -\frac{\mathrm{d}\Psi}{\mathrm{d}t} \tag{7.5.1}$$

式中,¥称为磁链。

当线圈的几何形状不变,并且它的周围不存在铁磁性物质及其他通电线圈的情况下,由毕-萨定律,线圈中的电流 I 在空间产生的磁感应强度 B,与其通过的 I 成正比,因此磁链 $\Psi$ 也与 I 成正比,即 $\Psi \propto I$ 。以 L 为比例系数,则 $\Psi$ 与电流 I 可写成如下关系式:

$$Ψ=LI$$

或写成 $L=Ψ/I$ (7.5.2)

比例系数 L 与线圈的大小、几何形状及线圈匝数有关,而与电流 I 无关,称为线圈的自感系数,简称自感。

由式(7.5.2)和自感电动势定义式(7.5.1)还可以写为

$$\mathscr{E}_L = -\frac{\mathrm{d}\Psi}{\mathrm{d}t} = -\frac{\mathrm{d}(LI)}{\mathrm{d}t}$$

当线圈的匝数、大小、几何形状都不变时, L 可以看成常量, 有

$$\mathscr{E}_L = -L \frac{\mathrm{d}I}{\mathrm{d}t} \tag{7.5.3}$$

上式表示,自感电动势 $\mathcal{E}_L$ 在数值上与线圈中电流随时间的变化率成正比。将式(7.5.3)改写成如下形式:

$$L = -\frac{\mathcal{E}_L}{\mathrm{d}I/\mathrm{d}t} \tag{7.5.4}$$

这个关系式可以作为各种大小和形状线圈的自感 L 的定义式。

根据式(7.5.4)可知,在国际单位制中 L 的单位为 $V \cdot s \cdot A^{-1}$ (伏特秒每安培)它的专有名称为"亨利",简称"亨",用"H"表示。在自感系数较小的情况下,还可以用 $mH(毫亨),\mu H(微亨)$ 表示,它们之间的关系为

文档:自感与互感 磁场能量

MATE

$$1 H = 10^3 \text{ mH} = 10^6 \mu \text{H}$$

由式(7.5.3)还可以确定线圈中 $\mathcal{E}$ ,的方向与电流变化的 关系。

若线圈中的电流 I 随时间增加,即 $\frac{dI}{dt} > 0$ ,则 $\mathcal{E}_{L} = -L \frac{dI}{dt} < 0$ , $\mathcal{E}_{L}$ 与电流方向相反,显示出 $\mathcal{E}_{L}$ 企图阻止电流 I 的增大;若 $\frac{dI}{dt} < 0$ ,则 $\mathcal{E}_{L} = -L \frac{\mathrm{d}I}{\mathrm{d}L} > 0$ ,显示出 $\mathcal{E}_{L}$ 企图阻止电流 I 的减小。在以上两种情 况下, $\mathscr{E}_{L}$ 都是反抗 I 的变化的,所以式(7.5.3)中 $\mathscr{E}_{L}$ 的方向与 $\frac{\mathrm{d}I}{\mathrm{d}L}$ 符号相反。

例题 7-3

如图 7-9 所示,在一个包含电感线圈的电路中,首先将开 关S掷于1处,确定电流随时间变化的关系。在电流达到稳定 值后,再将开关S掷于位置2处,确定电流随时间变化的函数 关系,设电源电动势为 $\mathcal{E}$ ,电阻为 R 的线圈的自感为 L。

解:(1) 当 S 掷于 1 处后, 电流并不能立刻 从零达到稳定值 $\mathcal{E}/R$ , 而是需要一个过程, 这个过程叫暂态过程,而这个过程是线圈中 自感电动势为抵抗电流的变化而引起的,在 电流达到稳定值前,自感电动势一直存在。 在暂态过程中应用欧姆定律,得

$$\mathscr{E} + \mathscr{E}_L = IR \quad \overrightarrow{\mathbf{g}} \quad \mathscr{E} - L \frac{\mathrm{d}I}{\mathrm{d}t} = IR$$

将其整理为

$$\frac{\mathrm{d}I}{I - \mathcal{E}/R} = -\frac{R}{L} \mathrm{d}t$$

考虑到开始时 t=0 时,I=0,对上式取定积 分得

$$\int_{0}^{I} \frac{\mathrm{d}I}{I - \mathscr{E}/R} = \int_{0}^{\iota} - \frac{R}{L} \mathrm{d}t$$

积分后并整理得

$$I = \frac{\mathscr{E}}{R} (1 - e^{-\frac{R}{L}t})$$

这就是电流 随时间增加 的函数关系。

图 7-9 例题 7-3 图

上式括号中的第二项是随时间减小的,当时 间足够长时该项趋于零,电流 I 趋于稳定值 $\mathcal{E}/R$ 。而 I 达到稳定值所需时间与 L/R 值 有关,L/R 小所需时间短,L/R 大所需时间 长。图 7-10 就反映了这种情况。

图 7-10 通电时 I-t 关系图

(2) 当电流达到恒定值后,再将开关 S 掷于位置2处,此时组成一个新的回路,而 自感电动势 $-L\frac{dI}{dt}$ 则是回路中唯一的电动势。由欧姆定律,有

$$-L\frac{\mathrm{d}I}{\mathrm{d}t} = RI \quad \text{id} \quad \frac{\mathrm{d}I}{I} = -\frac{R}{L}\mathrm{d}t$$

设 S 掷于位置 2 处的时刻为零,t=0,相应 $I=\frac{\mathcal{E}}{\mathbf{p}}$ ,对上式取定积分,得

$$\int_{Z/R}^{I} \frac{\mathrm{d}I}{I} = -\frac{R}{L} \int_{0}^{L} \mathrm{d}t$$

积分并整理后得

$$I = \frac{\mathscr{E}}{R} e^{-R\iota/L}$$

这就是电流随时间减小的关系式。由此可见,I 是随时间按指数规律衰减的。衰减所需时间与 L/R 值有关,L/R 小则所需时间短,L/R 大则所需时间长。图 7-11 就反映了这种情况。

图 7-11 断电时 I-t 关系图

例题 7-4

图 7-12 所示为半径为 $R_1$ 和 $R_2$ 、高为 l 的两个同轴金属薄圆筒,设两个圆筒有相同的电流 I,但方向相反,两圆筒间充满磁导率为 $\mu$ 的磁介质。求同轴圆筒单位长度的自感系数 L。

解:分析可知,两圆筒之外 B=0,两圆筒之间 $B=\frac{\mu I}{2\pi r}$ 。为了得出自感系数 L,须首先得到 B 穿过的筒间任意截面 abcd 的磁通量 $\Phi$ 。选截面 abcd,则 B 传过该截面的磁通量为

$$\boldsymbol{\Phi} = \int_{S} \boldsymbol{B} \cdot d\boldsymbol{S} = \int_{R_{1}}^{R_{2}} \frac{\mu I l}{2\pi r} dr = \frac{\mu I l}{2\pi} \ln \frac{R_{2}}{R_{1}}$$

利用式 (7.5.2) 得 $L_{\&} = \frac{\Phi}{I} = \frac{\mu l}{2\pi} \ln \frac{R_2}{R_1}$ 故单位长度上的自感系数 L'为 $L' = \frac{L_{\&}}{l} = \frac{\mu}{2\pi} \ln \frac{R_2}{R_1}$

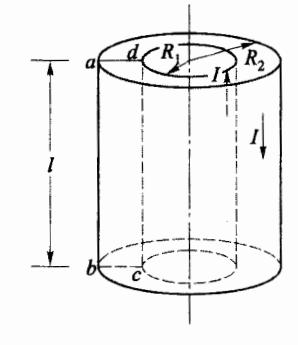
图 7-12 例题 7-4图

例题 7-5

求一密绕螺线管的自感系数。设螺线管长 $l=15~{\rm cm}$ ,共 绕 $N=500~{\rm E}$ 匝线圈 ,其面积 $S=2~{\rm cm}^2$ ,如图 $7-13~{\rm M}$ 示。

解:由于螺线管的长度与截面的直径相比要 大许多,除螺线管端口附近外,可以认为 B 是均匀的。设螺线管通有电流 I,因此可知

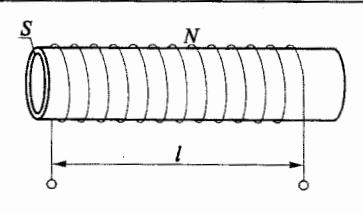
图 7-13 例题 7-5图

管内的 $B = \mu_0 \frac{N}{l}I$ , 磁链

$$\Psi = N\Phi = NSB = \frac{\mu_0 N^{2} IS}{l}$$

再根据式(7.5.2)有

$$L = \frac{\Psi}{I} = \frac{\mu_0 N^{2} S}{l} = \frac{\mu_0 N^{2} Sl}{l^{2}} = \mu_0 n^{2} \Delta V$$

式中, $\Delta V = Sl$ 为螺线管的体积,n = N/l 为单位长度上螺线管的匝数,代人相应的数值,于是得

$$L = \frac{\mu_0 N^2 S}{l} = (4\pi \times 10^{-7}) \times \frac{500^2 \times 2 \times 10^{-4}}{0.15} \text{ H}$$ $$= 4.2 \times 10^{-4} \text{ H}$$

自感现象在电工及无线电技术中应用广泛,自感线圈是交流 电路和无线电设备中的基本元件。它和电容器一起可以组成谐 振电路或滤波器。利用线圈具有阻碍电流的特性,可以用它稳定 电路中的电流。但有些情况下自感现象又十分有害,例如当切断 自感系数 L 很大的自感线圈的电源时,会产生很强的自感电动 势,足以击穿线圈本身的绝缘保护,或在电闸处产生电弧,可能会 造成不必要的损失,应加以避免。

7.5.2 互感现象与互感系数

当一个线圈中的电流发生变化时,将在它临近的其他线圈中产生感生电动势。这种现象称为互感现象,由此产生的感生电动势称为互感电动势。

如图 7-14 所示,两个相对放置的线圈 $L_1$ 和 $L_2$ ,设线圈 $L_1$ 和 $L_2$ 通过的电流分别为 $I_1$ 和 $I_2$ 。设 $I_1$ 产生的磁场通过线圈 $L_2$ 的磁链为 $\Psi_{21}$ ,由毕-萨定律,线圈 $L_1$ 中的电流 $I_1$ 在空间产生的 $B_1$ 与 $I_1$ 成正比,因此 $\Psi_{21}$ 也与 $I_1$ 成正比,同理 $\Psi_{12}$ 应与 $I_2$ 成正比,即

$$\frac{\Psi_{21} = M_{21}I_1}{\Psi_{12} = M_{12}I_2} \tag{7.5.5}$$

上式中的 $M_{21}$ 和 $M_{12}$ 为比例系数,分别称为线圈 2(或 1) 对线圈 1(或 2)的互感系数,简称互感,其大小与两个线圈的相对位置,各自的大小、匝数、几何形状以及两线圈周围介质磁导率的分布有关,而与线圈中是否存在电流无关。

理论及实验都证明 $M_{21} = M_{12}$ ,所以可以用共同的互感系数 M来表示,M 的单位与自感系数 L 的单位相同,也为 H(亨利)。

当线圈 $L_1$ 中的电流 $I_1$ 发生变化时,将在线圈 $L_2$ 中产生互感电动势 $\mathcal{E}_{21}$ ;同理,线圈 $L_2$ 中的电流 $I_2$ 发生变化时,在线圈 $L_1$ 中产

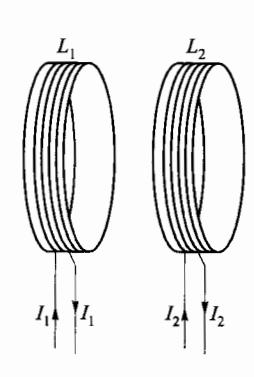
图 7-14 互感现象

生的互感电动势为 $\mathcal{E}_{ij}$ 。根据法拉第电磁感应定律可以得

$$\mathcal{E}_{21} = -\frac{\mathrm{d}\Psi_{21}}{\mathrm{d}t} = -\frac{\mathrm{d}(MI_{1})}{\mathrm{d}t} = -\left(M\frac{\mathrm{d}I_{1}}{\mathrm{d}t} + I_{1}\frac{\mathrm{d}M}{\mathrm{d}t}\right)$$ $$\mathcal{E}_{12} = -\frac{\mathrm{d}\Psi_{12}}{\mathrm{d}t} = -\frac{\mathrm{d}(MI_{2})}{\mathrm{d}t} = -\left(M\frac{\mathrm{d}I_{2}}{\mathrm{d}t} + I_{2}\frac{\mathrm{d}M}{\mathrm{d}t}\right)$$

当两个线圈的相对位置,各自的大小、匝数、几何形状以及两线圈周围介质磁导率的分布均不变时,互感系数 M 为一常量。于是有

$$\left\{\begin{array}{l}\mathcal{E}_{21} = -M \frac{\mathrm{d}I_{1}}{\mathrm{d}t} \\ \mathcal{E}_{12} = -M \frac{\mathrm{d}I_{2}}{\mathrm{d}t}\end{array}\right.$$

(7.5.6)

由上式可以看出,当两个线圈中电流的时间变化率相等时,两个线圈的互感电动势就相等。而其中一个线圈中的电流时间变化率不变时,互感系数 M 越大,在另一个线圈中产生的感应电动势也就越大,因此 M 的大小反映了两个线圈相互影响的能力。

两个线圈的互感系数 M 与它们各自的自感系数 L 有一定的联系。如果在两个线圈中,任意线圈里的电流所产生的磁场都能无遗漏地穿过另一个线圈,两线圈的互感系数 M 与两线圈各自自感系数 $L_1$ 和 $L_2$ 间有如下关系:

$$M = \sqrt{L_1 L_2}$$

若只有部分磁场穿过对方线圈,则

$$M = K \sqrt{L_1 L_2}$$

式中, K为比例系数, 其取值范围在0~1之间。

一般情况下,两个线圈间的互感系数 M 可以通过实验测量,对于简单的情况也可以通过计算求出。

互感原理在无线电及电工学中有广泛应用,常见的变压器、 感应发电机、感应线圈等都是应用了互感原理。