7.1 电流与磁场

欲使某条导线 l 有电流通过,导线内部就应该存在一个电 场。欧姆定律的微分形式告诉人们,导线中各点处的电流密度是 与导线中各点处的电场强度成正比的,即 $J=\sigma E$ 。若要在导线中 建立电场,导线两端须存在电势差。设想有两个导体 A 和 B,如 图 7-1(a) 所示, 其中导体 A 带有正电荷, 导体 B 带有等量的负 电荷,导体 A 的电势 $V_A$ 高于导体 B 的电势 $V_B$ , $V_A - V_B > 0$ 。当用 导线 l 将导体 A 和 B 连接后,在导线 l 内就建立起了电场,电场 的方向循导线由导体 A 指向 B,如图 7-1(b)所示。在静电场的 作用下,依然假设电流是正电荷定向移动产生的,则导体 A 所带 的正电荷循着导线迁移到导体 B,这个过程使导线中有电流通 过。但是,这个电流随着导体 A 所带正电荷不断减少,导体 B 所 带正电荷不断增加,导体 A、B 间的电势差愈来愈小,直至为零 $(V_A - V_B = 0)$ 。这个过程非常短暂。导线 l 和导体 $A \setminus B$ 一起成为 等势体,导线内的电场和电流也随之消失。而要想在导线 l 中维 持一个恒定的电流,就需要在导线内维持一个恒定的电场,而要 达到这一点,导体 A、B 中电荷分布的差异就应该保持恒定, A、B 间的电势差就应维持恒定。为做到这些,可以考虑在导线通有电 流时,设法给失去正电荷的导体 A 及时补充正电荷,设法使迁移 到导体 B 上的正电荷及时排除掉,使连接导线两端 A 、B 两个导 体的电荷分布维持一个动态平衡。

可以设想在导体 A、B 间再用导体连接另外一个线路,在此 称其为线路2,如图7-1(c)所示。在线路2中存在着一种能不断

文档:法拉第

____ 文档:亨利

← ✓ 文档:电源及其电动势

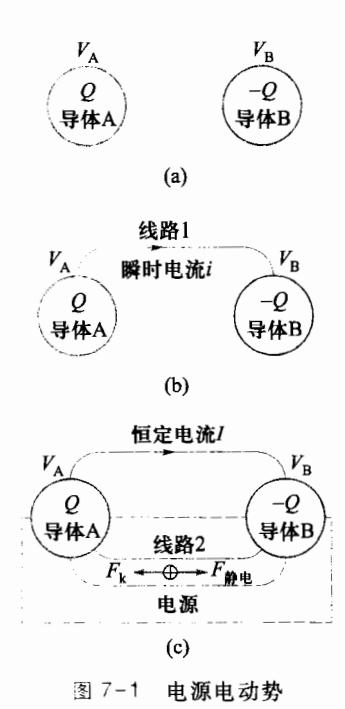
地将迁移到导体 B 上的电荷重新搬回到导体 A 上的力,这种力绝不可能是静电力,因为导体中的静电力只能使正电荷从高电势处向低电势处移动,而在线路 2 中,搬运正电荷由 B 向 A 的过程,是使正电荷的电势从低位向高位移动的过程,是逆着静电场力方向的,因此,这个力只能是某种非静电力 $F_k$ 。 $F_k$ 在逆着静电场移动正电荷过程中,克服导体中的静电场力对正电荷做功,使其他形式的能量转化成提供给线路 1(导线 l)的电能。

因此,将能够提供非静电力、把其他形式的能量转化成电能的装置叫作电源,相应的导体 A 和 B 称为电源的正、负极。而将与两极相连的导体线路 1 (1 中有一定的电阻值) 称为外电路,而将导体线路 2(线路 2 也有一定的电阻值 R,称为电源内阻) 称为电源的内电路。在外电路中,正电荷在电场力的作用下由高电势处向低电势处流动;在内电路中,正电荷在非静电场力的作用下由低电势处向高电势处流动。

人们将在内电路中,由负极到正极搬运单位正电荷时非静电 力所做的功定义为电源电动势,即

$$\mathcal{E} = \frac{W_{\#}}{q} \tag{7.1.1}$$

按功的定义

$$\mathbf{W}_{\sharp} = \int_{(\mathbf{h})^{-}}^{+} \mathbf{F}_{\mathbf{k}} \cdot d\mathbf{l} = \int_{(\mathbf{h})^{-}}^{+} q\mathbf{E}_{\mathbf{k}} \cdot d\mathbf{l},$$

于是有

$$\mathscr{E} = \frac{W_{\parallel}}{q} = \int_{(\phi)}^{+} E_{\mathbf{k}} \cdot d\mathbf{l}$$

(7.1.2)

定义 $E_k$ 为非静电场场强,它仅仅存在于电源内部,在电源外 $E_k$ =0。 $\mathcal{E}$ 是表征一个电源特性的重要的物理量,是标量,但是为 了标明在电路中电源维持电流方向的作用,规定 $\mathcal{E}$ 的方向为电源 内部电势升高的方向,其单位与电势的单位相同,为 V( 伏特) 。 若一个回路中处处都有非静电力存在,则整个回路的电动势为

$$\mathscr{E} = \oint \mathbf{E}_{\mathbf{k}} \cdot \mathbf{d}\mathbf{l} \tag{7.1.3}$$

对于这种情况,将在下节的感生电动势中予以介绍。