6.5 物质磁性的简介

6.5.1 物质的磁性

凡是放入磁场能够显示出磁性的介质都称作磁介质,几乎所有的物质都是磁介质。磁介质放入磁场中显示磁性的现象称为磁化现象。磁化后的磁介质会产生附加的磁感应强度 B'。而磁介质内部的磁感应强度 B,是真空(或空气)中的磁感应强度 B。与 B'的矢量和,即

$$\boldsymbol{B} = \boldsymbol{B}_0 + \boldsymbol{B}' \tag{6.5.1}$$

在相同的 $B_0$ 下,不同介质的 B 并不相同,这是由介质本身的 属性所确定的。为表述这种差异,引入相对磁导率 $\mu_L$ ,其定义为

$$\mu_{\rm r} = \frac{B}{B_0} \tag{6.5.2}$$

$\mu_r$ 是一个量纲为 1 的量。对不同种类的磁介质进行相同方式的检测发现,引入某些磁介质后,如铬、铂、氮、氧等,磁感应强度 B 的数值将增加,即 $B>B_0$ ,此时 $\mu_r>1$ ,此类介质产生的附加磁感应强度 B'与真空中的磁感应强度 $B_0$ 的方向一致,这类磁介质称为顺磁质;还有某些磁介质,如铜、铋、硫、氢、金、银等,引入磁场后,会使原磁感应强度变小,即 $B<B_0$ ,此时 $\mu_r<1$ ,此类介质所产生的附加磁感应强度 B'恰好与原来真空中的磁感应强度 $B_0$ 方向相反,这类磁介质称为抗磁质;还有一类磁介质,如铁、钴、镍等,这类磁介质引入磁场后的磁感应强度远远大于未引入以前,即 B>> $B_0$ ,此时 $\mu_r>1$ ,这类磁介质称为铁磁质。

前两种磁介质的磁性很弱,又称为弱磁性材料;而后一种由于具有很强的磁性,又称为强磁性材料。表 6-1 列出了某特定温度下某些磁介质的相对磁导率。

表 6-1 在某特定温度下某些磁介质的相对磁导率

磁性	物质(特定温度)	相对磁导率 $\mu_{\rm r}$
顺磁材料 ( $\mu_{\rm r}>1$ )	铁、铵、矾(4 K)	1.483 0
	铁、铵、矾(90 K)	1.002 13
	液氧(90 K)	1.001 52(1.007 69)
	铂(293 K)	1.000 26
	铝(293 K)	1.000 022(邓法金 1.000 016 5)
	钠(293 K)	1.000 007 2
	氧(气态)(293 K)	1.000 001 9

文档:磁介质

NOTE

续表
磁性	物质(特定温度)	相对磁导率 $\mu_r$
抗磁材料 ( $\mu_r < 1$ )	铋(293 K)	0.999 834
	汞(293 K)	0.999 971
	银(293 K)	0.999 974
	碳(金刚石)(293 K)	0.999 979
	铅(293 K)	0.999 982
	岩盐(293 K)	0.999 986
	铜(293 K)	0.999 990
铁磁材料 ( $\mu_r \gg 1$ )	纯铁	5\u00d7103(最大值)
	硅钢	7\u00d7102(最大值)
	坡莫合金	1\u00d7105(最大值)

顺磁质与抗磁质的本质

磁介质具有不同磁性质的根源在于分子所具有的磁矩。

分子是由原子构成,而原子是由若干个电子及原子核构成,每个电子都有围绕原子核的旋转和绕自身轴的旋转,每种旋转都会形成一种环状的电流,根据 6.4.2 节所述,任何一个环状电流都相当于一个磁偶极子,都会产生一个磁矩 m。通常称电子绕核旋转产生的磁矩为"轨道"磁矩,称电子自旋产生的磁矩为自旋磁矩。

原子中所有轨道磁矩及其自旋磁矩的矢量和构成原子的磁矩,而分子中所有原子磁矩的矢量和构成分子磁矩,分子磁矩又称为分子的固有磁矩。与分子固有磁矩相对应的环状电流称为分子电流。由于分子内部的微观结构各不相同,有些分子存在着固有磁矩,有些分子则不存在固有磁矩。在没有外磁场作用的情况下,没有固有磁矩的分子构成的磁介质对外不显示磁效应。即使是那些本身具有固有磁矩的分子所构成的磁介质,在无外磁场时,亦无磁效应。这是由于在一块磁介质中存在着无数多个分子,在无外磁场时,由于分子的热运动,各个分子的固有磁矩的取向杂乱无章,各不相同,即分子的固有磁矩沿各个方向取向的概率是相同的。如果在磁介质中任取体积元 $\Delta V$ ,则其中所有分子磁矩的矢量和为零,即 $\Sigma m=0$ 。因此这类分子构成的磁介质在无外磁场时,对外不显磁性。

当将磁介质引入外磁场 $B_0$ 后,对于其中分子存在固有磁矩的磁介质来说,磁介质中所有分子磁矩都将同时受到外磁场 $B_0$

所给予的磁力矩的作用,迫使分子磁矩向外磁场 $B_0$ 方向转向。 $B_0$ 越强,分子所受的磁力矩就越大,沿 $B_0$ 方向排齐的程度就越高。但是,分子的热运动会极力阻碍和破坏这种排齐,磁介质温度越高,这种破坏能力就越强。在温度和外磁场强度不变时,两者能达到一种平衡状态,此时磁介质中任意体积元 $\Delta V$ 内,所有分子磁矩的矢量和不再为零,即 $\sum m \neq 0$ 。沿外磁场方向,其宏观表现是磁介质出现了顺磁现象。但是在一般温度下,分子热运动对磁介质的影响要比外磁场 $B_0$ 产生的影响大,所以,磁介质的顺磁性表现得非常弱。一旦外磁场 $B_0$ 撤销,磁介质就不显磁性了。

抗磁性的现象来源于磁介质中轨道磁矩与自旋磁矩在外磁场下产生的进动效应。现以某个轨道磁矩在外磁场中运动情况,定性说明磁介质抗磁性的原因,如图 6-25 所示,对轨道磁矩 m 来说,总有相对应的角动量 L,两者之间的关系为

$$m = -\frac{e}{2m}L$$

式中,e 和 m 分别表示代表电子的电荷量和质量。当将磁介质引入外磁场 $B_0$ 后,m 将受一力矩作用,根据式(6.4.8)该力矩为

$$\boldsymbol{M} = \boldsymbol{m} \times \boldsymbol{B}_0 = -\frac{e}{2m} \boldsymbol{L} \times \boldsymbol{B}_0$$

在这个力矩的作用下,磁矩 m 将以外磁场 $B_0$ 为轴做进动。进动使整个分子电流绕 $B_0$ 旋转,其结果又产生了一个附加的环形电流 i',对应 i'的附加磁矩 $\Delta m$ 。无论角动量 L 与外磁场 $B_0$ 的 夹角 $\alpha$ 是大于或小于 $\pi/2$ ,总是导致附加磁矩 $\Delta m$ 与 $B_0$ 的方向相反,如图 6-25 所示。这就是磁介质产生抗磁性的原因。

一般来说,在任何一种磁介质中,都并存着产生顺磁和抗磁的两种机制。但抗磁性均很弱,常常被磁介质的顺磁性所掩盖,只有那些没有固有磁矩的磁介质的抗磁效果才能显现出来。

6.5.3 磁化强度矢量

衡量介质磁化程度的物理量,称为磁化强度,用M表示,对于顺磁质来说,M等于磁化后介质内部单位体积 $\Delta V$ 中所有分子磁矩的矢量和,即

$$M = \frac{\sum m}{\Delta V} \tag{6.5.3}$$

M 与外磁场 $B_0$ 方向相同。而对于抗磁质来说, M 等于磁化后介

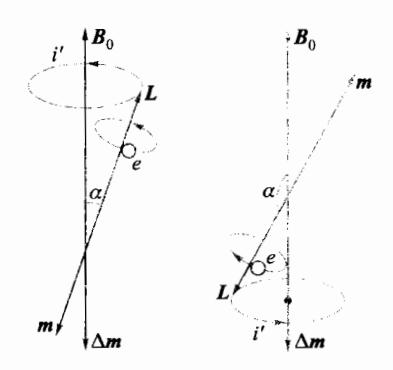
图 6-25 外磁场中电子的进动

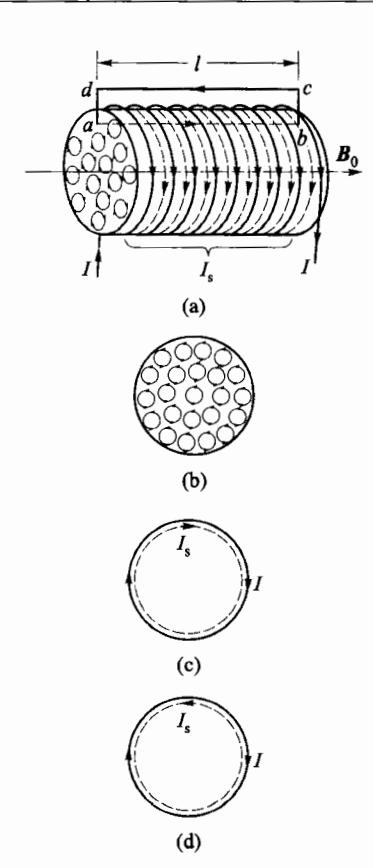
图 6-26 磁介质磁化时分子电流 的分布

质内部单位体积 $\Delta V$ 中所有附加磁矩 $\Delta m$ 的矢量和.即

$$M = \frac{\sum \Delta m}{\Delta V} \tag{6.5.4}$$

式中,M 的单位是 $A \cdot m^{-1}$ (安每米)。在均匀磁化后的顺磁质中,分子的磁矩趋向外磁场 $B_0$ 的方向排列,抗磁质中的附加磁矩与 $B_0$ 反向排列,与分子磁矩相对应的分子电流和与附加磁矩相对应的附加电流都将有规则地排列。

为简单起见,以一段沿轴向均匀磁化后的柱形介质为例,如图 6-26 所示,在柱的截面上可以看到规则排列的分子电流,每个电流旋向相同,因而相邻电流由于彼此电流的方向相反而被抵消。这样导致在截面内部没有电流,而在截面边缘处,尚存有未被抵消的电流,所有这样的电流连接在一起,就构成了环绕截面的电流,由于这种电流起源于分子电流,并且仅出现在介质表面上,所以称为表面分子电流。又由于这种电流不同于自由电荷形成的电流,即其中任何一个运动电荷本身都不能沿着柱体的表面环绕一周,它只能体现电流的磁性质,也不能产生电流的热效应,所以又称表面束缚电流,该电流用 1、表示。

同样的理解可以应用于抗磁质,得出抗磁质磁化后也存在 I₄,只不过其方向与顺磁质中 I₅ 的方向相反,如图 6-26 所示。

6.5.4 M 与 B 的关系

1. M 与 i, 的关系

若以 $i_s$ 表示柱形磁介质单位长度上的表面分子电流,即分子电流线密度,则长为 $\Delta l$ 的柱体上的表面分子电流为 $\Delta I_s = i_s \Delta l$ 。表面分子电流产生的磁矩 $m = \Delta I_s Se_n$ ,式中 $e_n$ 为柱体端面的单位法线矢量,S为柱体的截面积,这个m还应等于柱体内所有分子磁矩 $m_i$ 的矢量和,即 $m = \sum_i m_i = \Delta I_s Se_n$ 。

根据式(6.5.3),得到M与i,的关系为

$$M = \frac{\sum_{i} m_{i}}{\Delta V} = \frac{\Delta I_{s} S e_{n}}{S \Delta l} = \frac{\Delta I_{s}}{\Delta l} e_{n} = i_{s} e_{n}$$

(6.5.5)

上式表示,M 在数值上等于单位长度上的表面分子电流 i.。

要进一步得出 M 与 $I_s$ 的关系,可以考察 M 的环路积分。对于一个沿轴向均匀磁化的磁介质,其内部各点处有相同的 M。现过柱体内、外选一矩形回路 abcda (图 6-27),其中 ab 段的全部, bc 和 da 段的部分位于磁介质外部,在磁介质外部 M=0.故 M 沿

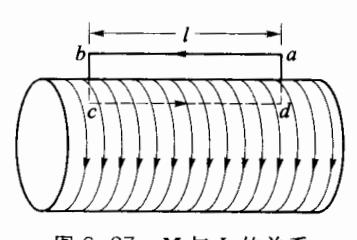
图 6-27 M 与 L 的关系

这些路径积分为零。bc 和 ad 位于磁介质内部的部分又与 M 垂直,故 M 沿位于磁介质内部路径积分为零。而在 cd 段中 M 是均匀的,并与积分路径同向,M 可以表示成数值量 M。根据 $M=i_s$ ,于是有

$$\oint_{abcda} \mathbf{M} \cdot d\mathbf{l} = \int_{a}^{b} \mathbf{M} \cdot d\mathbf{l} + \int_{b}^{c} \mathbf{M} \cdot d\mathbf{l} + \int_{c}^{d} \mathbf{M} \cdot d\mathbf{l} + \int_{d}^{a} \mathbf{M} \cdot d\mathbf{l}$$ $$= \int_{c}^{d} \mathbf{M} \cdot d\mathbf{l} = \int_{c}^{d} i_{s} dl = i_{s} l = I_{s}$$ $$\oint_{abcda} \mathbf{M} \cdot d\mathbf{l} = I_{s} \quad (6.5.6)$$

式中,1,为所选回路包围的表面分子电流。

式(6.5.6)的物理意义为: M 的环流(或称 M 的环路积分)等于环路所围的表面分子电流。上式虽是从均匀磁场的特殊情况下得到的,但它是普遍规律。

2. M 与 B 的关系

磁化后介质内部的磁感应强度 B 是由传导电流 $I_a$ 和表面分子电流 $I_s$ 共同产生的。以 $B_o$ 表示传导电流 $I_a$ 激发的磁感应强度,B'表示表面分子电流 $I_s$ 激发的磁感应强度,则 $B=B_o+B'$ 。对各向同性的顺磁质, $B_o$ 与 B'同向,抗磁质 $B_o$ 与 B'反向。

现以顺磁质为例,根据例题 6-7,在螺绕环中传导电流产生的磁感应强度为

$$B_0 = \mu_0 n I_d = \mu_0 i_d$$

式中,n 为单位长度上线圈的匝数, $i_a = nI_a$ 则表示单位长度上的传导电流。类似的方法,可以得出

$$B' = \mu_0 i$$

式中, $i_s$ 为单位长度上的表面分子电流。由于在数值上 $M = i_s$ ,所以又有 $B' = \mu_0 M$ ,依据式 (6.5.2) 有 $B_0 = \frac{B}{\mu_r}$ ,则 $B = \frac{B}{\mu_r} + \mu_0 M$ ,整理后得

$$B = \frac{\mu_0 \mu_r}{\mu_r - 1} M \tag{6.5.7}$$

式中,令 $\mu = \mu_0 \mu_r$ ,称为磁导率;令 $\chi_m = \mu_r - 1$ ,称为磁化率。由于 $\mu_r$ 是一个量纲一的量,对于顺磁质,有 $\mu_r > 1$ ,所以 $\chi_m > 0$ ;对于抗磁质,有 $\mu_r < 1$ ,所以 $\chi_m < 0$ 。于是由式(6.5.7)写出 M 与 B 的关系式为

$$\boldsymbol{B} = \frac{\mu}{\chi_{-}} \boldsymbol{M} \tag{6.5.8}$$

对于顺磁质,B与M同向;对于抗磁质,B与M反向。