
文档:电场强度通量与 高斯定理
图 5-12 电场线示意图
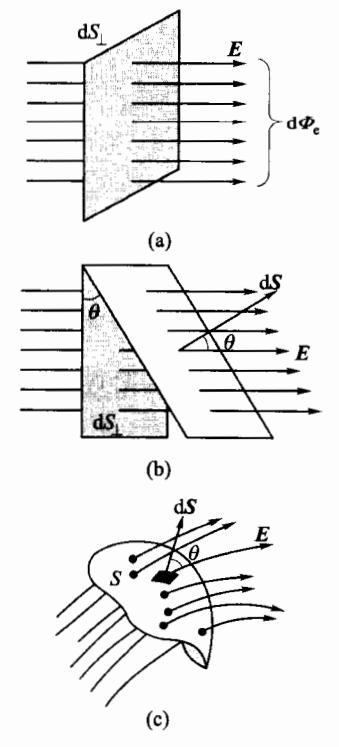
图 5-13 电场强度通量示意图
5.2.1 电场线和电场强度通量
为了形象地描述电场强度在空间的分布,引入一组带有方向的曲线(图 5-12),正的检测电荷在曲线上任意一点受力的切线方向,表示该点的场强方向;空间某区域内曲线的疏密反映出该区域电场强度的大小,这样的曲线称为电场线(曾用名:电力线)。描述静电场的电场线总是由正电荷出发,终止于负电荷或无穷远处。在没有电荷的空间,电场线既不会产生,也不会中断。由于空间任意点处的电场强度只有一个方向,所以电场线也不会相交。
为了将电场线的疏密与空间场强大小联系起来,对电场线的疏密作如下规定:过电场中任意点,作一垂直于该点电场线的面元 dS⊥ ,若通过此面元的电场线数为 dΦe ,则该点的电场强度大小为
E=dS⊥dΦe(5.2.1)
应该强调,电场中并非真实地存在这样的场线,所以也不存在真实的电场线数,电场线的引入,仅仅为了形象地描绘场强的空间分布。由式(5.2.1)看到 E 的取值不一定是正整数。
电场是一个矢量场,而矢量场可以引入矢量通量的概念。描述静电场的电场线,在一定的单位制下,做了式(5.2.1)的约定后,可以将通过一个面的电场线数称为通过该面的电场强度通量,用符号 Φe 表示,通过某面元 dS 的电场强度通量用 dΦe 表示。一般说来,在相同场点处,通过面元的电场强度通量与面元的大小有关,在一定面元大小下,面元的取向不同,通过的电场强度通量也不同。为了把面元的大小和方位都表现出来,因此引入面元矢量 dS,dS 的方向与面元平面垂直。
如图 5-13(b) 所示,通过面元 dS 的电场强度通量与通过该面元 dS 在垂直电场 E 的平面内的投影 dS1 的电场强度通量是一样的,即 dΦe=EdS1=EdScosθ 。按矢量标积的写法,通过面元 dS 的电场强度通量,可以记为 dΦe=E⋅dS 。电场强度通量是个标量,但仍有正、负之分。定义某点的电场强度 E 与该点的面元矢量的夹角 θ 为锐角时,电场强度通量为正;当 θ 为钝角时,电场强度通量为下;当 θ 为钝角时,电场强度通量为零。
如果要确定通过图 5-13(c)所示的不均匀电场中一个有限曲
面 S 的电场强度通量,应首先将曲面分割成许多小面元 dS,然后分别求出通过每个小面元的电场强度通量 dΦe ,再将所有 dΦe 叠加起来,就得到通过该曲面 S 的电场强度通量,即
Φe=∫dΦe=∫SE⋅dS
按数学规定,在电场中确定通过任意形状的闭合曲面的电场强度通量时,该闭合面上各面元矢量 dS 都指向闭合曲面外法线方向,电场线穿入曲面,电场强度通量为负;穿出曲面,电场强度通量为正。
以下分析在静电场中电场线通过一个闭合曲面的电场强度通量。
5.2.2 静电场中的高斯定理
德国科学家高斯,对物理学的发展做出了卓越的贡献。著名的高斯定理给出了电场中某个假想闭合曲面的电场强度通量 Φ 。和该曲面所包围净电荷之间的联系。
对静电场中高斯定理的讨论,本书采用由特殊到一般的方法进行。如图 5-14 所示,假设一正电荷 q 被包围在一个闭合 S 中。为了确定通过该闭合曲面的电场强度通量,以 q 为中心作一半径为 r 的球面 S',点电荷在球面 S'上各点的场强 E 由式(5.1.5)确定,由于球面上各点到 q 的距离处处相等,且 S'面上任意点的面矢量,都与该点场强 E 方向一致,通过球面 S'的电场强度通量为
Φe=∫dΦe=∮S′E⋅dS′=∮S′4πε0r2qdS′=4πε0r2q∮S′dS′=4πε0r2q4πr2=ε0q(5.2.2)
由图 5-14 还可以看出,通过球面 S'的电场强度通量,恰好是通过它外面的那个任意形状的闭合曲面 S 的电场强度通量。若q 为正,则电场强度通量 Φe>0 ,电场线由闭合面内穿出;若 q 为负,则 Φe<0 ,电场线穿入闭合面。习惯上称这种任意形状的闭合面为高斯面。
如图 5-15(a),若点电荷 q 处于高斯面之外,由于电场线的连续性,q 所产生的电场线穿入高斯面的部分,能够完全从高斯面穿出,故位于高斯面之外的电荷在该面产生的电场强度通量为零,即
Φe=∮SE⋅dS=0(5.2.3)
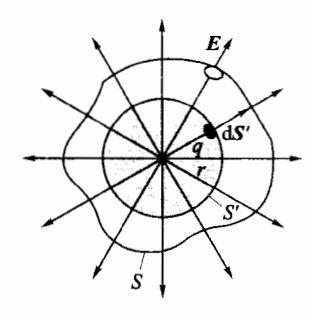
图 5-14 静电场中的高斯定理
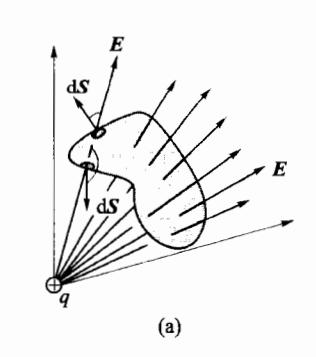

图 5-15 高斯定理导出
设想,在静电场中作高斯面 S,如图 5-15(b)所示,在面内有电荷 q1,q2,⋯,qi,⋯,qn ,共 n 个;在高斯面之外有电荷 qi+1,qi+2,⋯,qj,⋯,qk ,共 k 个。在高斯面上任意处的电场强度 E 是由空间存在的所有电荷共同产生的,即
E=i=1∑nEi+n+1∑kEj
(5.2.4)
式中, Ei∖Ej 分别为高斯面内第 i 个、高斯面外第 j 个电荷在高斯面上某点处产生的场强。通过该点所对应面元 dS 的电场强度通量为 dΦe=E⋅dS ,则通过整个高斯面 S 的电场强度通量为
Φe=∮SE⋅dS=∮S(i=1∑nEi+j=n+1∑kEj)⋅dS=∮Si=1∑nEi⋅dS+∮Sj=n+1∑kEj⋅dS
依式(5.2.3)可知,上式右边第二项为零;又依式(5.2.2)可得到通过闭合曲面的电场强度通量为
Φe=∮SE⋅dS=ε01i=1∑nqi
(5.2.5)
这就是高斯定理的数学表达式,其物理含义为:在真空中通过任意闭合曲面的电场强度通量,等于该曲面所包围的所有电荷的代数和与真空中介电常量 ε0 的商,而与闭合面外的电荷无关。
如果闭合曲面 S 所包围的体积为 V 的物体,电荷在该物体上是连续分布的,若电荷的体密度为 ρ ,则高斯定理表达式(5.2.5)右边的求和应写成对电荷分布空间的体积分,即
Φe=∮SE⋅dS=ε01∫VρdV(5.2.6)
利用数学中的高斯定理,有
∮SE⋅dS=∫V∇⋅EdV
于是得
∇⋅E=ρ/ε0(5.2.7)
数学上称 ∇⋅E 为矢量场 E 的散度,式(5.2.7)称为高斯定理的微分形式。其物理意义为:在一个微小的局域内,若电场的散度不为零时,即 ∇⋅E=0 ,必然有电场线从该小局域中发出或终止于其内,所以小局域必有场的源头。有源头的矢量场称为有源场,真空中的静电场即是一种有源场。
高斯定理的基础是库仑定律和场强叠加原理。但是,高斯定理是在场强与距离平方成反比 (DE×r21) 严格成立条件下得到
的。近代实验证明,库仑定律中 E∝r2+ϵ1 ,式中的 ϵ≤(2.7±3.1)×10−6 。因此,在静电场中两者是等效的。应该指出,库仑定律是超距作用的一种表现,它仅对静电场有效,而高斯定理在整个电磁理论中都有效。
此外,当已知静电场具有某种形式的对称分布时,选择适当的高斯面,利用静电场中的高斯定理,就可以十分简便地求出该电场在空间的具体分布。
例题 5-4
已知一半径为R的均匀带电球壳,所带总电荷量为q,求其电场分布。
解:如图 5-16 所示,首先考虑球壳外各点的场强分布。在球壳外任选点 P,过 P 点作一与带电球壳同心、半径为 r(r>R) 的球形高斯面 S。该高斯面面积为 4πr2 ,由于电荷分布具有球对称性,所以电场也具有球对称性,即在半径相同的球面上,各点电场强度大小是相等的,方向沿半径向外 (q 为正电荷时),即 E 的方向与所对应的面元矢量的方向是一致的 (cosθ=1) ,电场强度通量应为
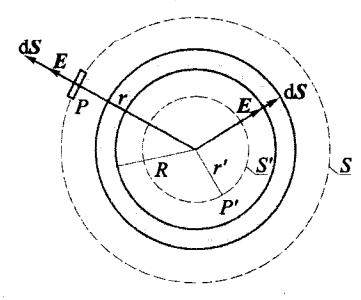
图 5-16 例题 5-4图
Φe=∮SE⋅dS=∮SEcosθdS
=E∮SdS=4πr2E
该高斯面所包围的电荷为球面所带电荷 q。由高斯定理式(5.2.5)得
4πr2E=ε0q
所以,在带电球面外各点的电场强度为
E=4πε0r2qer(r>R)
此式表明,均匀带电球壳外各点的电场 强度,与球心处放置相等电荷量的点电荷所 产生的电场场强是一样的。
当所选择的场点位于带电球壳外,且又紧靠着球壳时,即 r≈R 时,则
E=4πε0R2qe,
当将场点选择在带电球壳内任意点 P'时,过P'作一半径为 r′(r′<R) ,面积为 4πr′2 的同心高斯面。同理,由于电荷及电场分布具有球对称性,所以高斯面上各处的电场强度的大小均相等,设其为 E',并沿半径向外,与高斯面上各点处面元 dS 的方向一致。因此通过该高斯面的电场强度通量为
Φc=E′⋅4πr′2
但是,由于高斯面位于带电球壳内部,所围电荷为 Σq=0 ,因此由高斯定理得
E′⋅4πr′2=0
故 E'=0。以上结果表明,均匀带电球壳内 场强处处为零。
例题 5-5
求半径为 R, 所带电荷量为 q 的均匀带电球体的电场强度的空间分布。
解:由于带电球体的电荷分布具有球对称性,所以利用高斯定理,可以十分简便地求出电场强度的空间分布。
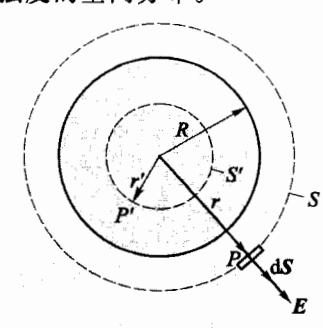
图 5-17 例题 5-5图
如图 5-17 所示,当所考察的点 P 位于带电球体之外时,过点 P 取同心球面为高斯面,由于电荷分布具有球对称性,所以在高斯面上,各点处电场强度 E 的数值都相等,并且在高斯面上的各点处,高斯面的法线方向与 E 的方向均相同,因此通过该高斯面的电场强度通量为
Φe=∮SE⋅dS=4πr2E(r>R)
由高斯定理可得
E=4πε0r2qer(r>R)
可知,球外任意点处的场强,等于球心处点 电荷 q 所产生的场强。
当场点位于球内任一点 P'时,以球心为中心,过 P'点作一同心球面 S'为高斯面,通过 S'面的电场强度通量为
Φe=∮S′E′⋅dS′=4πr′2E′(0<r′≤R)
高斯面所包含的电荷量为
q′=ρ34πr′3
式中 ρ=(4/3)πR3q 为电荷体密度,故
q′=R3qr′3
由髙斯定理得 4πr′2E′=ε0R3qr′3 ,即
E′=4πε0R3qr′er=3ε0ρr′er(0<r′≤R)
例题 5-6
求电荷线密度为λ的"无限长"均匀带电直线周围的电场分布。
解:由对称性可知,"无限长"带电直线的电场,在位于与直线垂直的平面内,电场线呈辐射状,即电场线只能沿径矢方向。在平面上距带电直线相等各点处 E 的数值相等,即电场线具有轴对称性。现以该带电直线为轴,作一半径为 r、长度为 l 的圆柱形高斯面,如图 5-18 所示,高斯面两个底垂直于带电直线,则其电场强度通量为
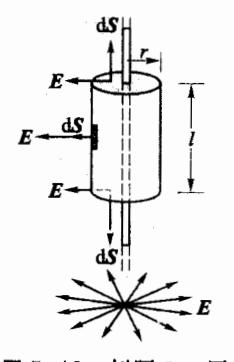
图 5-18 例题 5-6图
Φe=∮SE⋅dS
=∫上底E⋅dS+∫下底E⋅dS+∫侧面E⋅dS
上式中上、下底面的法线矢量 n 与 E 垂
上式中上、下底面的法线矢量 n 与 E 垂直,对电场强度通量没有贡献,即电场强度通量为零;而侧面的法线矢量方向与 E 处处一致,且侧面各点处 E 的数值为恒量,所以
Φe=∮SE⋅dS=∫MinE⋅dS=2πrlE
(5.2.8)
圆柱形高斯面所包含的电荷量 q=lλ ,
由高斯定理得 2πrlE=ε0λl ,即
E=2πε0rλ(5.2.9)
对于带正电荷的直线来说,场强的方向沿半 径向外。
本例题利用了"无限长"带电直线的电场具有轴对称性的特点,合理地选择了柱面形高斯面,因此,利用高斯定理十分简洁地求出了"无限长"带电直线产生电场的空间分布,与例题 5-1 所采用积分方法实现的场强叠加相比,要简单许多。
求"无限大"均匀带电平面产生的场强。设电荷面密度为 σ 。
根据对称性,可以确定带电平面所产生的电场是均匀的,并且垂直于平面,指向远离平面的方向(设该平面带正电荷)。如图 5-19 所示,选取一垂直于平面的柱形曲面为高斯面,高斯面的截面为 ΔS ,并且与带电面平行,其侧面面元矢量 dS 与电场 E 垂直,故通过侧面的电场强度通量为零。而由于高斯面两端面的外法线方向与该处的 E 方向一致,所以每个端面的电场强度通量为 EΔS ,而通过整个高斯面的电场强度通量为

Φe=∮SE⋅dS
=∫左端E⋅dS+∫右端E⋅dS+∫侧面E⋅dS
=2EΔS
高斯面所围电荷电荷量 ∑q=ΔSσ 。由高斯定理得
2EΔS=ε0ΔSσ
故
E=2ε0σ(5.2.10)
对于带电平面两侧所有各点,电场强度的数值都是相同的。尽管在实际中"无限大"的带电平面并不存在,但以上推导仍成立,因为对于一个实际带电平面来说,只要所考虑的场点不在带电平面的边缘附近,而且离平面的距离远小于平面本身的线度,就可以将实际平面视为"无限大"平面。
另外,带电平面两侧场强的方向恰好相反,即带电平面两侧的电场不连续,存在突变,其突变量 ΔE=2ε0σ−(−2ε0σ)=ε0σ 。该结论对于任意导体表面附近都成立。
5.2.3 静电场的环路定理


文档:环路定理与电势
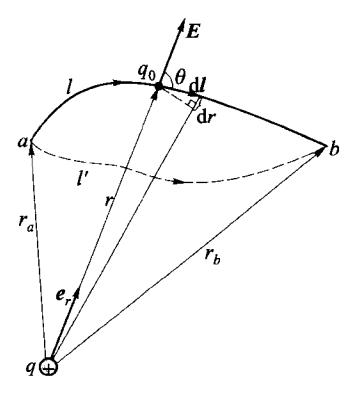
图 5-20 电场力的功
当位于静电场中的一个电荷,从一个位置移动到了另一个位 置,就意味着静电场力对该电荷做了功。以下,从静电场做功的 特点,讲一步考察静电场的性质。
如图 5-20 所示,在一个点电荷 q 产生的电场中,将一正的检 验电荷 q0 从 a 点沿任意路径 l 移动到 b 点,电场力对 q0 做功为
Wab=∫abF⋅dl=q0∫abE⋅dl
(5. 2. 11)
点电荷 q 的场强分布 E=4πε0r2qe , 代入式(5.2.11)得电场力对 q0 做的功为
Wab=4πε0qq0(ra1−rb1)
(5. 2. 12)
上式表明,静电场力所做的功与路径无关,仅与始末位置有 关。q0 由 a 到 b 不管是沿路径 l 或沿路径 l'还是沿其他任何路 径,所做的功都是完全一样。由式(5.2.11)得
∫abE⋅dl=q0Wab
(5. 2. 13)
上式称为,将单位电荷由点 a 移动到点 b 电场力所做的功。同 样,这个功仅仅取决于单位电荷的始末位置,而与所经过的路径 无关。所以,将单位电荷沿任意闭合回路移动一周,静电场所做 的功为零,即
∮lE⋅dl=0(5.2.14)
上式左边是静电场 E 沿某闭合回路的环路积分, 称为静电 场 E 的环流。静电场 E 的环流为零,表明静电场是保守场,静电 场力是保守力。式(5.2.14)是静电场的一个重要性质。







