1.5 角动量定理与角动量守恒定律

本节讨论的是从牛顿第二定律导出的第三个定理和守恒律。

1.5.1 质点角动量定理与角动量守恒定律

1. 质点角动量

行星绕太阳运动、人造地球卫星绕地球运动、电子绕原子核运动等都是质点绕一个定点运动的情况,机器的轮子中各个质点的运动则是质点绕固定轴运动的情况,在这类运动中,由于速度的方向不断变化,用动量来描述很不方便,需要引入一个新的物理量——角动量来描述运动,其必要性还在于,在上述这类运动中,质点受到外力的作用,动量守恒定律不再适用,但只要质点所受的力满足一定条件,角动量守恒往往能够成立,这就为问题的解决提供了极大方便。

质点的角动量又称动量矩。如图 1-33 所示,质量为 m 的质点以速度 v 运动,质点相对坐标原点 O 的位置矢量为 r,r 与 v 构成如图所示的平面。质点 m 相对 O 点的角动量定义为质点的位矢 r 与质点动量 p=mv 的矢量积,用 L 表示为

$$\boldsymbol{L} = \boldsymbol{r} \times \boldsymbol{p} = \boldsymbol{r} \times \boldsymbol{m} \boldsymbol{v} \tag{1.5.1}$$

角动量是矢量,角动量的大小为

$$L = |L| = rp\sin \theta = rmv\sin \theta \tag{1.5.2}$$

式中 $\theta$ 是 r 与 v 两矢量间的夹角。L 的方向垂直 r 与 v 构成的平面,其指向可按右手螺旋定则确定:先以右手四指并拢指向 r 的方向,再让四指弯曲以小于180°的角度转向 v 的方向,则拇指的指向即为 L 的方向(图 1-33)。显然,质点的角动量不但与质点本身的动量有关,还与质点相对坐标原点的位置有关。一般来说,同一运动质点相对不同参考点具有不同的角动量。谈到质点的角动量必须指明参考点的位置。从这里可以理解动量与角动量定义的不同。

在国际单位制中,角动量的单位为 $kg \cdot m^2 \cdot s^{-1}$ (千克二次方米每秒)。

2. 力矩

力矩的概念是与转动相联系的,力矩可以改变物体的转动状态。力矩的定义与上面的动量矩(即角动量)相似。如图 1-34 所示,设有一力 F 作用于 A 点,A 点相对坐标原点 O 的位置矢量为 r,r 与 F 构成如图所示的平面。力 F 相对 O 点的力矩定义为力 F 作用点的位矢 r 与力 F 的矢量积,用 M 表示为

$$\mathbf{M} = \mathbf{r} \times \mathbf{F} \tag{1.5.3}$$

图 1-33 质点的角动量

图 1-34 力矩的定义

力矩是矢量,力矩的大小为

$$\mathbf{M} = |\mathbf{M}| = rF\sin\theta = Fd \tag{1.5.4}$$

式中, $\theta$ 是r与r 两矢量间的夹角。 $d=r\sin\theta$ 是力r 的作用线与 O 点的垂直距离,称为力r 的力臂。r 的方向垂直r 与r 构成的平面,其指向按右手螺旋定则确定,在图 1-34 情形下,r 指向平面的上方。与质点的角动量一样,力矩不但与力本身有关,还与力的作用点相对参考点的位置有关,同样一个力相对不同参考点具有不同的力矩。谈到力矩也必须指明参考点的位置。注意理解力与力矩定义的不同。

在国际单位制中,力矩的单位为 N·m(牛顿米)。

3. 质点角动量定理

牛顿第二定律式(1.2.1)指出,质点动量 p=mv 的时间变化 $=\frac{\mathrm{d}p}{\mathrm{d}t}$ 等于质点所受的合外力 $=\mathrm{F}$ 。下面来看质点角动量 $=\mathrm{F}\times mv$

的时间变化率与什么物理量有关。将 $L$ 对时间求导数,有

$$\frac{dL}{dt} = \frac{d}{dt}(r \times mv) = \frac{dr}{dt} \times mv + r \times \frac{d(mv)}{dt} = v \times mv + r \times F$$

由于 $v \times mv = 0, r \times F = M$ , 所以有

$$\mathbf{M} = \frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t} \tag{1.5.5}$$

此式表明:质点所受合外力矩等于质点角动量对时间的变化率,这称为质点的角动量定理。式(1.5.5)是质点角动量定理的微分形式。前面已经提到,角动量和力矩都要指明参考点的位置。在上面的推导中,角动量和力矩用到的是同一个位矢r,这表明角动量和力矩都是相对坐标原点的。但由于上面并没有对位矢r的大小作出限制,也就是说,坐标原点的位置是可以任选的。所以式(1.5.5)是对任意参考点成立的。只需注意,角动量和力矩必须是相对同一个参考点。

将式(1.5.5)改写成

$$\mathbf{M} \, \mathrm{d}t = \mathrm{d}\mathbf{L} \tag{1.5.6}$$

设 $t_1$ 时刻质点角动量为 $L_1$ , $t_2$ 时刻质点角动量为 $L_2$ ,对上式积分,得

$$\int_{t_1}^{t_2} \mathbf{M} dt = \mathbf{L}_2 - \mathbf{L}_1 \tag{1.5.7}$$

式中, $\int_{t_1}^{t_2} M dt$ 是描写合外力矩对时间累积作用的物理量,称为合外力对物体的冲量矩。在国际单位制中,冲量矩的单位为 $N \cdot m \cdot s$ (牛顿米秒)。式(1.5.7)表明:作用在质点上的冲量矩等于质点

角动量的增量,这是质点角动量定理的积分形式,也称为质点的冲量矩定理。同样要注意,其中的力矩和角动量都是相对同一参考点的。

4. 质点角动量守恒定律

由式(1.5.5)或式(1.5.7)可知,当质点所受合外力矩 M=0时,质点角动量 L=常矢量,这称为质点角动量守恒定律。

在中心力(也称有心力)场中,质点所受的力总是沿着质点与此中心(称为力心)的连线,如太阳对行星的万有引力、原子核对电子的静电引力等,尽管质点所受合外力不为零,但所受相对中心的合外力矩为零,因此质点相对中心的角动量是守恒的。

例题 1-16

如图 1-35 所示,在光滑桌面上,质量为 m 的小球系在轻绳的一端,绳子的另一端穿过中心 O 点处的小孔用手拉住。开始时,小球以速率 $v_0$ 做半径为 $r_0$ 的圆周运动。然后向下拉绳,使小球运动半径减小。求小球半径为 r 时的速率以及绳子拉力 r 对小球所做的功。

图 1-35 小球受有心力

解:小球受重力、桌面支持力以及绳子的拉力,三力相对0点的合力矩为零,因此,小球相对0点的角动量守恒。对于初态和末态来讲,小球速度方向与半径方向垂直,角动量守恒可写成

$$mv_0r_0 = mvr$$

由此得所求速率为

结果表明,小球半径减小,速率增大。绳子拉力对小球所做的功可按质点的动能定理求出:

$$W = \frac{1}{2}mv^{2} - \frac{1}{2}mv_{0}^{2} = \frac{1}{2}mv_{0}^{2} \left[ \left( \frac{r_{0}}{r} \right)^{2} - 1 \right]$$

绳子拉力对小球做功使小球动能增加。

例题 1-17

行星围绕太阳做椭圆轨道运动,太阳位于椭圆的一个焦点上。试证明行星相对太阳的位置矢量在相等时间内扫过相等的面积(此即开普勒第二定律)。

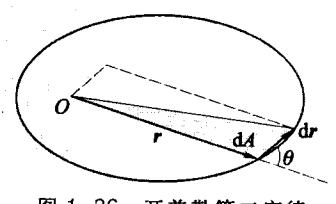
证:行星受太阳的万有引力为一有心力,故行 星相对太阳中心的角动量守恒。如图 1-36 所示, r 为行星某时刻的位矢, dr 为其 dt 时 间内的位移,计算

$|r \times dr| = rdr \cdot \sin \theta = 2dA$ 式中, dA 为行星位矢在 dt 时间内扫过的面

图 1-36 开普勒第二定律

积(图中阴影部分),行星位矢扫过面积的时间变化率为

$$\frac{\mathrm{d}A}{\mathrm{d}t} = \frac{1}{2} \frac{|\mathbf{r} \times \mathrm{d}\mathbf{r}|}{\mathrm{d}t} = \frac{1}{2} \left| \mathbf{r} \times \frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t} \right| \\ = \frac{1}{2m} |\mathbf{r} \times m\mathbf{v}| = \frac{1}{2m} |\mathbf{L}|$$

因为行星相对太阳的角动量守恒,|L| = 常量,所以 $\frac{dA}{dt}$ = 常量,即行星位矢在单位时间内扫过的面积为一常量,自然在相等时间内扫过相等的面积。证毕。

行星围绕太阳做椭圆运动,速度的大小和方向处在不断的变化中,因此其动量是不守恒的;但其角动量却是守恒的。由此也可以看出两个物理量的不同点以及引入角动量的必要性。另外,行星围绕太阳运动时的动能是不守恒的,但机械能是守恒的。

1.5.2 质点系角动量定理与角动量守恒定律

1. 质点系的角动量定理

设有一个由n个质点组成的质点系,其中第i个质点的质量为 $m_i$ ,相对坐标原点O的位矢为 $r_i$ ,速度为 $v_i$ ,角动量为 $L_i = r_i \times m_i v_i$ 。第i个质点所受来自系统外物体的合外力为 $F_i$ ,来自系统内其他质点的合内力为 $F_{\alpha i}$ 。对第i个质点应用角动量定理,有

$$\mathbf{r}_i \times (\mathbf{F}_i + \mathbf{F}_{p_i}) = \frac{\mathrm{d} \mathbf{L}_i}{\mathrm{d} t}$$

将上式对质点系内所有质点求和,有

$$\sum_{i=1}^{n} \mathbf{r}_{i} \times (\mathbf{F}_{i} + \mathbf{F}_{ \text{内} i}) = \sum_{i=1}^{n} \mathbf{r}_{i} \times \mathbf{F}_{i} + \sum_{i=1}^{n} \mathbf{r}_{i} \times \mathbf{F}_{ \text{内} i}\\ = \sum_{i=1}^{n} \frac{\mathrm{d} \mathbf{L}_{i}}{\mathrm{d} t} = \frac{\mathrm{d}}{\mathrm{d} t} \left( \sum_{i=1}^{n} \mathbf{L}_{i} \right)$$

式中, $\sum_{i=1}^{n} \mathbf{r}_{i} \times \mathbf{F}_{i}$ 为合外力矩,令 $\mathbf{M} = \sum_{i=1}^{n} \mathbf{r}_{i} \times \mathbf{F}_{i}$ ; 而 $\sum_{i=1}^{n} \mathbf{r}_{i} \times \mathbf{F}_{\mathbf{A}i}$ 为合内力矩,由于内力成对出现,对每一对内力来说,二者大小相等方向相反且作用在同一条直线上,力的作用线到坐标原点 $\mathbf{O}$ 的距离相同,所以每一对内力相对坐标原点 $\mathbf{O}$ 的力矩之和均为零,对所有内力矩求和自然也就为零,即 $\sum_{i=1}^{n} \mathbf{r}_{i} \times \mathbf{F}_{\mathbf{A}i} = \mathbf{0}$ ; $\sum_{i=1}^{n} \mathbf{L}_{i}$ 为质点系内各个质点角动量的矢量和,称为质点系的角动量,令 $\mathbf{L} = \sum_{i=1}^{n} \mathbf{L}_{i}$ 。

于是,上式写成:

$$\sum_{i=1}^{n} \mathbf{r}_{i} \times \mathbf{F}_{i} = \frac{\mathrm{d}}{\mathrm{d}t} \left( \sum_{i=1}^{n} \mathbf{L}_{i} \right) \quad \overrightarrow{\mathbf{g}} \quad \mathbf{M} = \frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t} \tag{1.5.8}$$

此式表明:质点系所受的合外力矩等于质点系角动量对时间的变化率。这称为质点系的角动量定理,属微分形式。同样要注意,合外力矩和质点系角动量都是相对同一参考点的。

仿照质点角动量定理的积分形式,对质点系同样有

$$\int_{t_{1}}^{t_{2}} \left( \sum_{i=1}^{n} \mathbf{r}_{i} \times \mathbf{F}_{i} \right) dt = \left( \sum_{i=1}^{n} \mathbf{L}_{i} \right)_{2} - \left( \sum_{i=1}^{n} \mathbf{L}_{i} \right)_{1}$$

或

$$\int_{t_{1}}^{t_{2}} \mathbf{M} dt = \mathbf{L}_{2} - \mathbf{L}_{1} \tag{1.5.9}$$

上式称为质点系的角动量定理,属积分形式。

2. 质点系的角动量守恒定律

由式(1.5.8) 或式(1.5.9) 可知,当质点系所受合外力矩 $M = \sum_{i=1}^{n} \mathbf{r}_i \times \mathbf{F}_i = 0$ 时,质点系角动量 $\mathbf{L} = \sum_{i=1}^{n} \mathbf{L}_i = 常矢量,这称为 质点系的角动量守恒定律。$

与动量守恒定律一样,角动量守恒定律也是自然界的普遍规律之一,不但适用于经典力学,也适用于高速与微观的情况。