8.3 电磁场的相对论变换
静止的电荷产生电场,而运动的电荷除产生电场外,还能产 小小丁 生磁场。运动具有相对性,所以电场与磁场之间必然存在着某种 变换关系。
A few characters appear in the image, but they are too faint and blurry to be deciphered and transcribed accurately. The image seems to contain some very light gray or near-white text on a white background, making it illegible.
- 电场与磁场的普遍变换关系
任意点电荷在空间某点处的电场为
式中,r 为点电荷到场点 P 的距离,e, 为点电荷到场点 P 的径矢 r的单位矢量
若该点电荷相对于观察者不是静止而是以匀速 v运动,则它 在空间P点处产生磁场为
(8.3.2)
式中r和e,均与式(8.3.1)中的r和e,意义相同。联立式 (8.3.1)和式(8.3.2)消去其中的 q 得
式中 为真空中的光速。式(8.3.3)是点电荷在低速运
动时得到的电场与磁场的关系,它也是惯性系间电场与磁场间普遍的转换关系。由于推迟效应的出现(所谓推迟效应,简单说,是空间场点处场强的变化会比运动电荷的变化落后一定的时间,电荷运动时会造成自身周围电场物质形态的变化,而不再是静止时不受干扰的对称均匀的球形分布),式中(8.3.1)和式(8.3.2)就不再适用了,需要应用相对论的变化规律对其进行修正。
2. 带电平面电场的变化规律
为了得到满足相对论情况下电场的变化规律,特对一个简单的模型进行分析。
(1) 在与电场方向相垂直的运动坐标系中
如图 8-5 所示,在两惯性系 和 K'中, 系以速度 沿 x' 轴向运动,在 系中的平行于 平面上固定着一对等大的矩形平行平面,平面的边长分别为 a 和 ,间距为 ,两平面所带电荷面密度分别为 和 ,平面的 边沿 轴放置。由于平面的面积很大,而两平面之间的距离 又很小,由高斯定理可知,两平面以外空间电场分布为零,而在除边缘外的两平面之间,场强是均匀并与平面垂直的,为
式中, 是沿z轴方向的单位矢量。在惯性系 K'中,这对平面是以 沿x'轴运动的,运动方向 与场强方向垂直。根据狭义相对论长度缩短的规律,可得在 K'系中测得的该平面的边长为
而平面的宽度 a 不变,因此该平面在 K' 系中的面积 S' 为
(8.3.5)
式中, 是 系中所测出该平面的面积,由于平面很大,所以在运动中两平面间的电场也是与平面垂直的。
应用高斯定理得两平面间的电场强度为
式中, ,Q 是平面所带电荷量,是一个相对论不变量,而 ,故
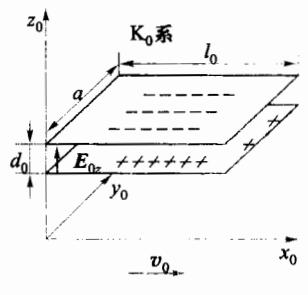
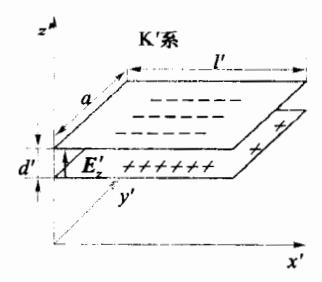
图 8-5 在与电场方向相垂直的 运动坐标系中带电平面电场的变 换规律
(8.3.7)
将式(8.3.7)代入式(8.3.6)得
(8.3.8)
此式表明,相对于与"静止"系中场强方向相垂直的运动坐标系中的观察者,他所测得的电场强度值变大,且随着相对速度的增大而增大。
(2) 在与电场方向相平行的运动坐标系中
现在假设固定在 系中的这对平面的表面是垂直 轴放置的(图 8-6),在 系中测得平面间的场强为
式中, 表示沿 轴的单位矢量。而在 K'系中观测到两平面以速度 沿垂直于平面方向运动,也就是沿着电场线的方向运动,尽管两面间的间距 变小,却不影响平面上的电荷面密度,而两平面间的电场又仅仅与平面上的电荷面密度有关,所以 K'系中测得两平面间的电场为
(8.3.10)
此式表明,沿着电场方向相平行的运动坐标系中的观察者, 观测到的电场与"静止"系中相同。
虽然上面的分析是借助两个平面电荷层模型得到,但式 (8.3.9)和式(8.3.10)的结果具有普遍性。对任意取向的电场强度 E,总可以在两个惯性系中对相同点 P 处的电场进行矢量分解,使之变成沿垂直于两惯性系运动方向 的分量 、 和平行于 的分量 和 ,即
(8.3.11)
由式(8.3.8)和(8.3.10)可得
E'_{\perp} = \gamma E_{0\perp} \\ E'_{\parallel} = E_{0\parallel} \end{cases}$$ (8.3.12) 式中,\gamma = \frac{1}{\sqrt{1-(v_0/c)^2}}
,注意 $\gamma \ge 1$ 。 由式(8.3.12)可以看出,当产生电场的场源运动时,电场强度在垂直运动方向上的分量将要发生变化。   图 8-6 在与电场方向相平行的坐标系中带电平面电场的变换规律    图 8-7 电磁场的相对论变换 #### 3. 电磁场的相对论变换 在一个惯性系中,静止的带电体只能产生电场,而在另外惯性系中,这个带电体就有可能处于运动状态,并形成某种分布的电流,因此它能够在产生电场的同时还产生磁场。利用相对论的变换关系,可以得到在不同惯性系中电磁场相对论变化的规律。 为了方便电磁场的变换,特选 $K_0$ 、K'和 K 三个惯性系,如图 8-7 所示。首先仍然将一对"无限大"带电平面固定在 $K_0$ 系中,电荷面密度分别为 $\sigma_0$ 和一 $\sigma_0$ ,带电平面平行于 $x_0y_0$ 平面。 $K_0$ 系以速度 $v_0$ 相对于 K' 系沿 x' 轴向运动;K' 系的速度 v 相对于 K 系 沿 x 轴向运动。已知在 $K_0$ 系中测得两带电平面间的电场为\boldsymbol{E}{0} = \boldsymbol{E}{0y} = \frac{\boldsymbol{\sigma}{0}}{\boldsymbol{\varepsilon}{0}} \boldsymbol{e}_{y0} \tag{8.3.13}
B_{0x} = B_{0x} = B_{0z} = 0
E_{y}' = \frac{\sigma'}{\varepsilon_{0}} = \frac{\sigma_{0}}{\varepsilon_{0} \sqrt{1 - (v_{0}/c)^{2}}} = \frac{E_{0y}}{\sqrt{1 - (v_{0}/c)^{2}}}
(8.3.15) 由于在 K'系中带电平面是运动的,因此形成了两层面电流。设面电流密度为 J',其大小为 $J' = \sigma' v_0$ ,其中带正电荷的平面所生电流沿 x'轴向;带负电荷的平面所生电流逆 x'轴向。在两层电流之间有磁场存在,为\mathbf{B}' = \mathbf{B}'{z} = \mu{0} J' \mathbf{e}'{k} = \mu{0} \sigma' v_{0} \mathbf{e}'_{k}
(8.3.16) 式中, $e'_i$ 为沿z'轴的单位矢量。 在 K 系中带电平面以 $u_x$ 沿 x 正向运动,由相对论速度变换式得u_{x} = \frac{v_{0} + v}{1 + (v_{0}v)/c^{2}}
(8.3.17) 式中 $,v_0$ 是带电平面对 K'系的速度大小,v 是 K'系相对 K 系的速度大小,v 在 K 系中测得每个带电平面所带电荷面密度为 $\sigma$ , $\sigma$ 与 $\sigma$ 。 关系为\sigma = \frac{\sigma_0}{\sqrt{1 - (u_x/c)^2}}
\sigma = \frac{\sigma'(1+v_0v/c^2)}{\sqrt{1-(v/c)^2}}
E_{y} = \frac{\sigma}{\varepsilon_{0}} = \frac{\sigma'(1 + v_{0}v/c^{2})}{\varepsilon_{0}\sqrt{1 - (v/c)^{2}}} = \frac{1}{\sqrt{1 - (v/c)^{2}}} \left(\frac{\sigma'}{\varepsilon_{0}} + \frac{v_{0}v\sigma'}{\varepsilon_{0}c^{2}}\right)
将式(8.3.15)代入上式,并将式(8.3.16)改写成 $v_0 = B'_*/(\mu_0 \sigma')$ 后也代入上式,并考虑到 $c^2 = 1/(\mu_0 \varepsilon_0)$ ,得E_{y} = \frac{E'{y} + vB'{z}}{\sqrt{1 - (v/c)^{2}}}
B_z = \mu_0 J = \mu_0 \sigma u_x
B_{I} = \frac{\mu_0 \sigma' v_0 + \mu_0 \sigma' v}{\varepsilon_0 \sqrt{1 - (v/c)^2}}
将式(8.3.16)代入上式,并将式(8.3.15)改写成 $\sigma' = E'_* \varepsilon_0$ 也代 人上式,并考虑到 $c = \frac{1}{\sqrt{\varepsilon_0 \mu_0}}$ ,得B_z = \frac{B'_z + (vE'_y / c^2)}{\sqrt{1 - (v/c)^2}} \quad (8.3.21)
仿照上面的方法,还可以让带电平面在 $K_0$ 系中平行于 $x_0y_0$ 平面并固定,从而得出相应电磁场的相对论变换。归纳起来在 K' 系和 K 系中电磁场的相对论变换为 E = E'E_{x} = E'_{x}
E_{y} = \frac{E'{y} + vB'{z}}{\sqrt{1 - (v_{0}/c)^{2}}}
E_{z} = \frac{E'{z} - vB'{y}}{\sqrt{1 - (v_{0}/c)^{2}}}
B_{x} = B'_{x}
B_{y} = \frac{B'{y} - vE'{z}/c^{2}}{\sqrt{1 - (v_{0}/c)^{2}}}
B_{z} = \frac{B'{z} + vE'{y}/c^{2}}{\sqrt{1 - (v_{0}/c)^{2}}} \quad (8.3.22)
Ex′=ExEy′=Ey−vBz1−(v/c)2Ez′=Ez+vBy1−(v/c)2Bx′=BxBy′=By+vEz/c21−(v/c)2Bz′=Bz−vEy/c21−(v/c)2(8.3.23)
应用以上变换形式具体讨论一下在 K。和 K'两惯性系之间 电磁场相对论的变换结果。已知在 $K_0$ 系中观测到电场 $E_0$ 和磁 场 $B_{0x} = B_{0y} = B_{0x} = 0$ , $K_0$ 系相对 K'以 $v_0$ 沿 x'轴运动, 利用式 (8.3.22)可得E′x=0,E′y=E0y1−(v0/c)2,E′z=0B′x=0,B′y=0,B′z=vE0y/c21−(v0/c)2}(8.3.24)
从上式可以看出,在相对带电平面静止的惯性系中只能观测 到电场存在,而在相对带电平面运动的惯性系中,不仅观测到有 电场存在而且还观测到有磁场存在。并且发现两个惯性系中电 场的大小是不同的。 从相对论变换可以看出,电场和磁场不再是各自独立的实体. 而是可以相互转换,密切联系的整体,是统一的电磁场的两个方面。 #### 思考题与习题 - 8.1 请写出麦克斯韦方程组的积分形式。 - 8.2 如图所示为一圆柱体的横截面,圆柱体内 有一均匀电场 E,其方向垂直纸面向内,E 的大小随时 间 t 线性增加, P 为柱体内与轴线相距为 r 的一点。 - (1) 想一想 P 点处位移电流密度的方向是向 哪里? - (2) P 点处感生磁场的方向又是向哪里?  题 8.2 图 8.3 如图所示. 圆形平行板电容器. 从 q=0 开始 ! 的方向和磁场强度的方向。  - 8.4 位移电流和传导电流有何相同与不同? - 8.5 为什么说麦克斯韦方程组是电磁理论的基 本方程? 它是怎样由实验定律经总结、推广、提高而一半径为 r(R, <r<R,)的球面的总位移电流。 得到的。在总结过程中, 麦克斯韦提出了哪些新 概念? - 的电压变化率为 $\frac{du}{dt}$ = 1.5×10<sup>5</sup> V·s<sup>-1</sup>,求该平行板电 容器中的位移电流? - 8.7 加在平行板电容器极板上的电压变化率为 1.0×10<sup>6</sup> V·s<sup>-1</sup>,在电容器内产生 1.0 A 的位移电流、 求该电容器的电容。 - 8.8 半径为 r的两块圆板组成的平行板电容器 充了电,在放电时两板间的电场强度的大小为E= $E_0 e^{-i/RC}$ ,式中 $E_0 \setminus R \setminus C$ 均为常量,求: - (1) 两板间的位移电流的大小; - (2) 其方向与场强方向。 - 8.9 一平行板空气电容器的两极板都是半径为 充电,试画出充电过程中,极板间某点 P 处电场强度 R 的圆形导体片,在充电时,板间电场强度的变化率为 dE/dt。若略去边缘效应,求两板间的位移电流。 - 8.10 给电容为 C 的平行板电容器充电,电流为 i=0.2e<sup>-t</sup>(SI单位),t=0时电容器极板上无电荷。求: - (1) 极板间电压 U 随时间 t 而变化的关系; - (2) t 时刻极板间总的位移电流 L (忽略边缘 - 8.11 一球形电容器,内导体半径为 R.,外导体 半径为 $R_2$ 。两球间充有相对介电常量为 $\varepsilon$ , 的介质。 在电容器上加电压,内球对外球的电压为 $u=u_n \sin \omega t$ 。 假设ω不太大,以致电容器电场分布与静态场情形近 似相同,求介质中各处的位移电流密度,再计算通过 - 8.12 一电荷为 q 的点电荷,以匀角速度 ω 做圆 周运动,圆周的半径为 R。设 t=0 时 q 所在点的坐标 8.6 平行板电容器的电容 C 为 20.0 $\mu$ F, 两板上 为 $z_0 = R$ , $y_0 = 0$ , 以 i j 分别表示 z 轴和 y 轴上的单位 矢量。求圆心处的位移电流密度 J。 - 8.13 一半径为 R=5.0 cm 的圆形平行板电容 器,在充电时,其中电场强度的变化率 $\frac{dE}{dt}$ = 1.0× 1012 V·m·s-1。求: 、 - (1) 两极板间的位移电流 1: - (2) 极板边缘的磁感应强度 B。 - 8.14 设电荷在半径为 R 的圆形平行板电容器 极板上均匀分布,且边缘效应可以忽略。把电容器接 在角频率为ω的简谐交流电路中,电路中传导电流的 峰值为 1。, 求电容器极板间磁场强度峰值的分布。 # 各章思考题与习题参考答案  #### 郑重声明 高等教育出版社依法对本书享有专有出版权。任何未经许可的复制、销售行为均违反《中华人民共和国著作权法》,其行为人将承担相应的民事责任和行政责任;构成犯罪的,将被依法追究刑事责任。为了维护市场秩序,保护读者的合法权益,避免读者误用盗版书造成不良后果,我社将配合行政执法部门和司法机关对违法犯罪的单位和个人进行严厉打击。社会各界人士如发现上述侵权行为,希望及时举报,本社将奖励举报有功人员。 反盗版举报电话 (010)58581999 58582371 58582488 反盗版举报传真 (010)82086060 反盗版举报邮箱 dd@ hep.com.cn 通信地址 北京市西城区德外大街 4号 高等教育出版社法律事务与版权管理部 邮政编码 100120 #### 防伪查询说明 用户购书后刮开封底防伪涂层,利用手机微信等软件扫描二维码,会跳转至防伪查询网页,获得所购图书详细信息。也可将防伪二维码下的 20 位密码按从左到右、从上到下的顺序发送短信至 106695881280,免费查询所购图书真伪。 #### 反盗版短信举报 编辑短信"JB,图书名称,出版社,购买地点"发送至 10669588128 防伪客服电话 (010)58582300 | | | | | - | |--|---|--|---|---| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | • | | | | | · | , | | | | | | | | | | | | : | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | • | | | | | | | | | | | | | | | | | | | | | | | | | | | |