6.6 有磁介质存在时的安培环路定理
由 6.3.3 节已知,真空中恒定磁感应场的安培环路定理为
在有磁介质存在的空间中,上式依然能成立,但是产生磁场的除了传导电流 外,还有表面分子电流 ,所以全部的电流为 。考虑两种电流的共同影响,式(6.5.9)改写成
(6.5.10)
由式(6.5.6),式(6.5.10)可以改写为 , 整理后得
式中, 是传导电流,为了方便,今后直接写成I,即
(6.5.11)
令
则式(6.5.11)改写成
式中,H 称为磁场强度,单位与 M 相同,都为 (安培每米),J 为传导电流密度。
式(6.5.13)为有磁介质存在情况下的安培环路定理,其物理意义为:在静磁场中,磁场强度 H 的环路积分等于通过闭合回路所围面积中所有传导电流的代数和。
6.5.6 B、M、H 三矢量的关系
在恒定磁场中,先后出现了 三个矢量。一般说来, 三者之间的关系是比较复杂的,在此仅讨论各向同性磁介质中的情况。由式(6.5.8)已知 的关系为
由式(6.5.12)已知 的关系为 , 利用
可以得到
同样可以得到
例题 6-9
如图 6-28 所示,在一个平均半径为r,截面半径为R,绕有N 匝线圈的螺绕环内,均匀充满各向同性的磁介质,磁介质的相对磁导率为 ,当线圈通过电流为I时,求磁场强度H和磁感应强度B。
例题 6-9 图
解:由于该螺绕环是一个理想的螺绕环,所以环内的磁场为均匀磁场,现沿环的平均周长取积分回路 l,由式(6.5.13)可得
均匀磁场中 H 为一常量,所以上式积分为
式中 为线圈密度。H的方向可以用右手螺旋定则确定。
求出 H 后,利用式(6.5.14)可以求得 或
例题 6-10
如图 6-29 所示,截面半径为 R 的无限长圆柱形导体,其外是一层相对磁导率为 ,内、外半径为 R、 的磁介质。当导体均匀通过电流 I 时,求导体和磁介质内的 H、B、M(在导体内 )。
解: 当电流为 I 的电流均匀通过导体时,导体任意横截面的电流密度大小为 。考虑到本题中磁场具有轴对称性,即在任意垂直于轴线的横截面上,所有磁场 H 数值相等的点,都位于以轴线为心的同心环上,因此可以在该平面上分别在导体和磁介质内取半径为r的同心圆环作为积分
回路 l,由式 ,通过积分,得到导体内的磁场强度的大小 为
例题 6-10 图
因此
由式(6.5.14)得到导体内的磁感应强度 的大小为
由式(6.5.15)得到导体内磁化强度 的大小为
用同样的方法可以得到磁介质内的 为
, ,
6.5.7 铁磁质
1. 铁磁质简介
铁磁质材料有如下特点:① 任何铁磁质材料都存在一个特征温度,该温度称为居里温度。当铁磁质材料在居里温度以下被磁化后,其内部所产生的附加磁感应强度 B',不仅与外磁场 方向相同,而且其数值也成百上千倍地大于 ;② 作为磁感应强度 B 与磁场强度 B 比值的磁导率 ,不再是一个常量, 与 B 有着更为复杂的关系;③ 在撤掉外磁场后,铁磁材料的磁性不能同时消除,如果要消除铁磁材料的磁性,须对其加适当的反向磁场。
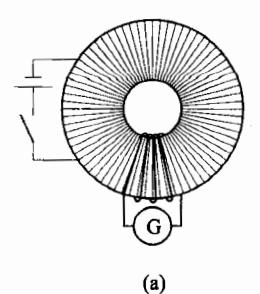
铁磁质的这些性质可以通过实验验证。将充满某种铁磁质的螺绕环与一个电流大小可以调节、电流方向可以控制的电源相连接,如图 6-30(a) 所示。通过改变电流 I ,并利用 H=nI( 由于单位长度上的匝数 n 为一常量),即知道了 I 就等于知道了磁场强度,再利用适当仪器探测出与 H 相对应的 B 值,即可绘出如图 6-30(b) 所示的 H-B 曲线。
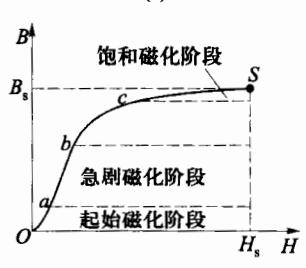
观察 H-B 曲线,由 O 到 S 这段曲线称为起始磁化阶段,而其中 Oa 阶段称为初始磁化阶段,ab 阶段称为急剧磁化阶段,到了 bc 阶段磁化开始变得缓慢,而在 cS 阶段磁感应强度 B 几乎不再随着 H 的增大而增大,则该阶段称为饱和磁化阶段。当磁化进入饱和状态后,逐步减小 H,B 随之相应地减小。但是,其过程并不沿起始磁化曲线返回,而是沿另外一条曲线 Sk 进行,如图 6-31(a) 所示。当H=0 时, ,称 为剩余磁感应强度。此时若撤去外磁场 H,铁磁质物质将成为一个永磁体。要去掉铁磁材料中的 ,也就是使铁磁材料退磁,须 H 反向。
当反向 H 的数值逐渐增加,直至 时,铁磁材料中的 剩磁才被去掉,即此时铁磁材料内的磁感应强度 称为矫
(b) 图 6-30 铁磁质的性质
顽力。继续反向增大 H 的数值,材料被反向磁化,直至材料又达到反向饱和态 S'。再逐步减小反向 H 的数值,材料中的 B 值随之减小,但过程仍不能沿着原曲线回溯,而是沿一条新的曲线由 S'到 e , e 点处 H 又一次为零,而材料又有了剩磁 -B , 其数值与 k 点处相当。再反转 H 使之为正值,并逐渐增大,反向的剩磁又被减小,直至 ,即 f 点处,材料中的磁化才完全消失。 与 数值相等,同为新顽力。进一步增大 H , 磁化沿曲线 f 的 f 到 f 点处,整个过程形成一闭合曲线。由于铁磁材料在磁化、退磁过程中,f 总是落后 f 的变化,故称这一曲线为磁滞回线。
不同的铁磁质材料,对应不同形状的磁滞回线。有的磁滞回线宽些,有的窄些。"宽"形曲线矫顽力 较大,剩磁 较强,通常将 值在 A·m-1范围的铁磁质叫作硬磁材料;而"窄形"曲线 较小,剩磁 小,通常将 的值在 A·m-1附近的铁磁质叫作软磁材料,如图 6-31(b)所示。另外,磁滞回线所围"面积"的大小反映了铁磁质在磁化、退磁过程中消耗能量的大小。一般说来,"面积"越大,消耗能量就越大。所以,在一般情况下,硬磁材料较软磁材料在磁化过程中要消耗更多的能量。
从磁滞回线还可以看出,材料中的 B 和 H 不再是单值线性 关系,利用 ,可以绘出图 6-32 所示 曲线,图上的 , 称为起始磁化率,对应图 6-30 H-B 曲线的 Oa 段, 。而 称为最大磁导率,对应 H-B 曲线中磁化最剧烈的 ab 阶段, 。由于磁化曲线 Oa 段是可逆的,所以 是铁磁质在高频下工作的主要参量,而 是设计低频电器的重要参量。
软磁材料用于制造电感元件,如变压器、镇流器、发动机、发电机、继电器等设备的铁芯,硅钢、坡莫合金和纯铁都属于软磁材料;硬磁材料,可以制造永磁铁、扬声器等,铬、钨、钴、镍等都属硬磁材料。
2. 铁磁质磁化的本质——磁畴
铁磁质的磁化依赖于原子中电子的自旋磁矩。在一种特殊的相互作用下(这种作用超出本书的范围,故不作介绍)使相邻原子的磁矩在一个小区域中耦合在一起,形成严格的平行排列。这个小区域称为磁畴。一个磁畴所占区域的大小为 10-18 ~ 10-12 m³,其中包含 1017~1021个原子。为了叙述方便,在此称磁畴中磁矩的方向为磁畴的方向。可以认为,整个铁磁材料是由这些大小不
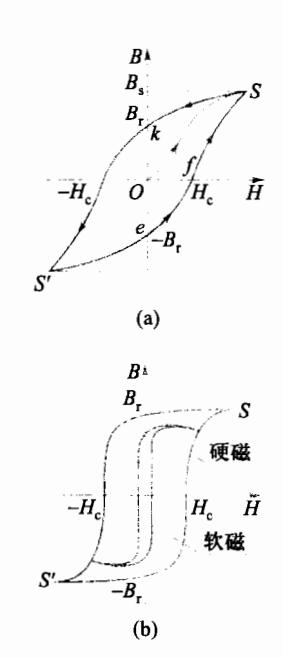
图 6-31 磁滞回线
图 6-32 H-μ 曲线

磁畴
式中
一、方向不同的磁畴构成,如图 6-33 所示,也正是由于磁畴的方 向各不相同,才使得未经磁化的铁磁质在宏观上不显磁性。
在铁磁质被磁化的过程中,磁畴会产生两种变化,其一是磁 畴壁的移动,其二是磁畴方向的转动。
当铁磁质开始磁化时,与外磁场方向相同或接近相同的磁畴 会挤占与其相邻的其他取向磁畴的领地。同向的磁畴壁向外移 动从而扩大自己的领地。图6-30中 H-B 曲线的 Oa 段就是反映 了这种过程,这时磁畴壁刚刚开始移动,尚属可逆阶段,倘若及时 撤除外磁场,磁畴还能回复到原来位置。当进一步增大 H,磁畴 壁的移动进一步加剧,此时磁畴壁的移动就不可逆了。这个过程 对应于图 6-30 中 H-B 曲线 ab 段。随 H 的不断增加,原来与外 磁场方向不同的磁畴也纷纷向外磁场方向转向。图 6-30 中 H-B 曲线的 bc 段反映出这种情况。图 6-33 示意出磁畴的运动。
当磁畴壁的移动和转向均已完成后,铁磁质就呈现出饱和状 态,此时由于所有磁矩几乎都向外磁场方向整齐地排列起来,所 以饱和磁感应强度 会远大于顺磁质中的 B。在撤掉外磁场 后,铁磁内部仍存在阻碍磁畴排列复原的力,这就是磁滞现象的 产生原因。
658 磁场的边界条件
描述磁场的两个物理量B和H,在两种不同的磁介质分界面 附近所满足的关系式称为磁场的边界条件。
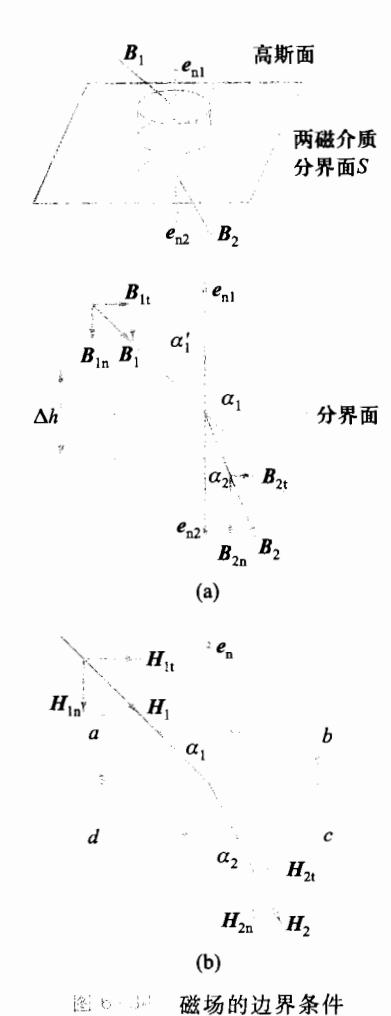
为了研究B的边界条件,作一个包含分界面S的扁平状柱形 高斯面,如图 6-34 所示。柱的高度为 , 极小, 趋近于零。 当 B 为有限值时,可以认为在高斯面的侧面上没有磁感应强度 B 通过。高斯面上、下两端面面积均为 , 很小, 以保证高斯面 所包含分界面S的部分很小,近似一个平面。高斯面上、下两端 面的单位法线矢量分别为 en、en。设穿过高斯面上端面的磁感 应强度为 与 的夹角为 ;穿过高斯面下端面的磁感应 强度为 , 与 的夹角为 , 应用磁场中的高斯定理, 得
式中, 、 分别表示 、 的法向分量,代人式(6.5.16)有
即
上式说明,在两种磁介质的分界面附近,磁感应强度的法线 方向是连续的。
为了研究 H 的边界条件,选择一个包含分界面的矩形积分回路 abcda,如图 6-34(b) 所示,其中 ab、cd 是矩形的长边,其长度为 l,l 很短以保证矩形回路所包含分界面的部分是一条直线,且与 l 边平行;bc、da 为矩形的高,其值极小,趋近于零,所以作为有限值的 H 沿这两条路径的积分为零;又由于闭合回路中没有包含传导电流,按照磁介质内的安培环路定理式(6.5.13),H 沿整个回路的积分为零,即
(6.5.18)
以 ,和 ,分别代表 ,和 ,的切向分量,即
将它们代入式(6.5.18)后,得
(6.5.19)
该式说明,在两种磁介质分界面处,其磁场强度 H 的切向分量连续。由 得
由式(6.5.20)、式(6.5.21)可知,两磁介质分界面附近 B 的切向分量及 H 的法向分量是突变的。
式(6.5.17)、式(6.5.19)、式(6.5.20)、式(6.5.21)即为磁场的边界条件。
下面对磁屏蔽进行讨论。由图 6-34 可知
利用式(6.5.17)、式(6.5.20)得
上式说明,当 B 穿过两介质的分界面时,其方向要发生变化,仿佛光线的折射。当磁感应强度 B 由相对磁导率 , 较大的磁介质
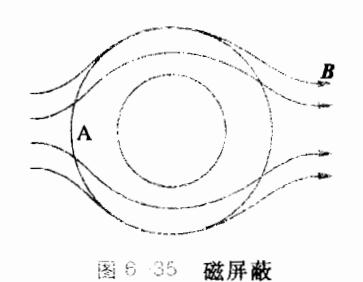
向相对磁导率 . 较小的磁介质传播时, B 与 e. 的夹角变小, B 更 靠近法线,反之则更远离法线。利用这种磁感应线的折射现象, 可以对 B 进行屏蔽。如图 6-35 所示, A 为软磁材料制成的空腔, 其相对磁导率 远大于空气中的相对磁导率 , 当将其放置在 有磁场存在的空气中时,由空气进入腔壁的 B 就会偏离法线,强 烈地收缩干腔壁内,而空腔内几乎没有磁场 B,因此起到了磁屏 蔽的作用。
思考题与习题
- 6.1 电流与电流密度有何不同,又有何联系?
- 6.2 电动势与电势差有何不同?
- 确定地球的磁偶极矩?
- 6.4 方程 dF=IdI×B 中的三个矢量,哪些矢量始 终正交?哪些矢量之间可以有任意角度?
- 6.5 磁感应线和电场线在表征"场"的物理性质 方面有哪些相似之处?
- 6.6 在磁场中,任意条给定的磁感应线上各点 处磁感应强度 B 的数值是否相同?
- 6.7 磁场的高斯定理反映了磁场的哪些性质?
- 6.8 利用安培环路定理,是否可以求出任何电 流回路在空间某处产生的磁感应强度?
- 6.9 把两种不同的磁介质放在磁铁的两个不同 名磁极之间,磁化后也成为磁体,但两极的位置不同, 如图所示,试指出哪一种是抗磁质?
S N S N N
顧 6.9 图
6.10 有两根铁棒,不论把它们的哪端相互靠 近,可以发现它们总是相吸引,你能得出什么结论?
6 11 地球北极的磁场 B=6×10-5 T, 如果想环赤 6.3 试猜测地球磁场形成的原因,用什么方法 道形成一电流来抵消这一磁场,试估算电流的大小和 方向。
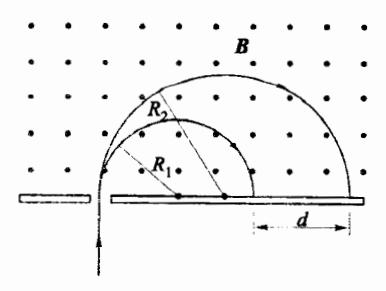
6 12 如图所示,有电流/沿导线从无限远处流 来,在 O 处转折 ,向无限远流去,求 、 点的磁 感应强度。P, 点在 MO 的延长线上,P, 点在载流线夹 角的角平分线上,且有 P, M=d, P, O=b, 若 I=1 A, d=0.50 m,b=0.60 m。试给出数值结果。
6.13 求图中(a)、(b)、(c)所示情况下 0 点的 磁感应强度。
题 6.13图
6.14 如图所示,有半径为 R 的薄无限长半圆柱面,沿母线方向均匀流过电流 I,求轴线上一点处的磁感应强度 B。
题 6.14 图
- 6.15 通有 20 A 电流的长直导线折成直角沿 x、y 轴放置,如图所示,试求:
- (1) 在 x 轴上距原点 O 为 2 m 的 Q 点处的 B 是 多少?
- (2) 在 z 轴上距原点 O 为 2 cm 的 P 点处的 B 是 多少?
题 6.15图
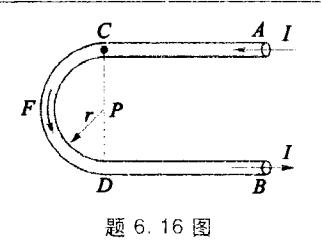
6.16 如图所示,一长导线在中部弯成图示形状,两端各延伸于很远处,圆弧半径为 r,通以电流 I 后,试求 P 点处的磁感应强度。
- 17 如图所示,自粗细均匀的圆形导线上的任意两点 P、Q 处沿半径方向引出两条直导线,而导线在无限远处与电源相接,证明圆形导线中心 O 点的磁感应强度为零。
题 6.17图
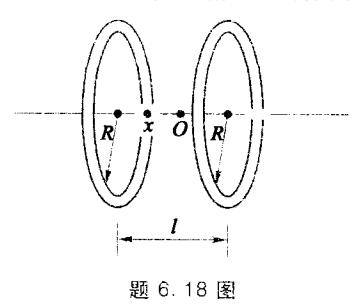
- 18 如图所示,两个半径为R的圆形线圈平行放置,相距为l,并通以流向相同的电流I(称为亥姆霍兹线圈),问在距离它们中心O点x处的磁感应强度是多少?并证明当l=R时,O点附近的磁场最为均匀。
-
- 19 如图所示,半径为 R 的绝缘盘均匀带电, 电荷面密度为 σ,圆盘绕垂直盘面通过盘心的轴以角 速度 ω 匀速转动,求轴线上任意点的磁感应强度和转 盘的磁偶极矩。
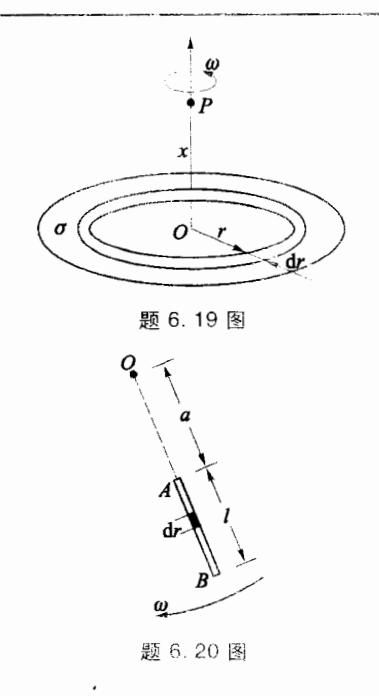
- 6.20 如图所示,均匀带电刚性绝缘细杆 AB,其长为l,电荷线密度为 ,绕垂直于直线的轴O以角速度 匀速转动(O点在细杆延长线上)。求:
- (1) 0 点处的磁感应强度;
- (2) 磁矩。
6.21 如图所示,一半径为 R 的球面上均匀分布 时,求在球心处的磁感应强度的大小。
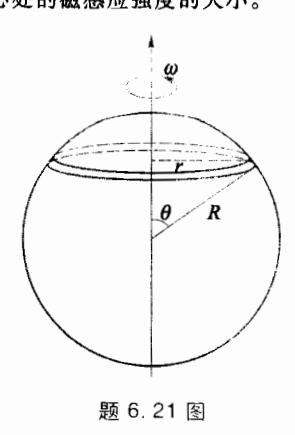
- 6.22 如图所示,有内半径为 、外半径为 的 无限长导体圆管,通以均匀的电流 1,求空间各区域的 磁感应强度。
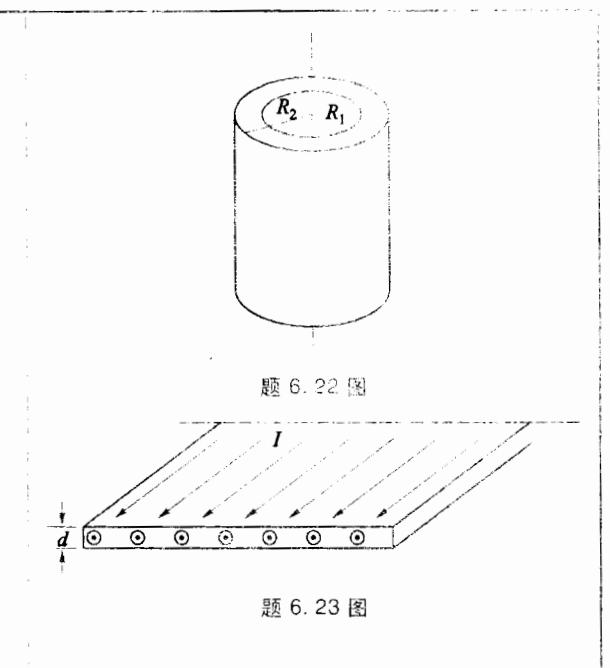
- 6.23 如图所示,一厚度为 d 的无限大导体平 板,沿同一方向通过均匀电流,电流密度大小为 J,求 | 导体内外的磁感应强度。
6.24 如图所示,一半径为 R 的无限长导体圆 柱,在距离轴线 d 处,挖掉半径为 的小圆柱, 着面密度为 σ 的电荷, 当它以角速度 ω 绕直径旋转 两圆柱轴线相互平行, 余下部分沿轴向流过均匀电 流,电流密度为 J,求:
- (1) 大圆柱轴线上的磁感应强度;
- (2) 空圆柱轴线上的磁感应强度;
- (3) 证明空圆柱内为均匀磁场。
题 6.24 图
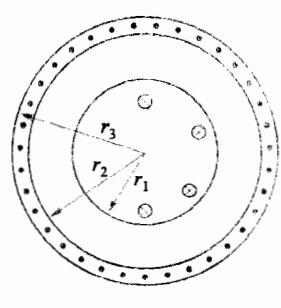
- 6.25 如图所示,一同轴电缆,内导体半径为 r1, 电流为 1; 外导体的内、外半径分别为 r2 和 r3, 电流为 1,但方向与内导体电流方向相反。同轴电缆的截面如 图所示,求以下各处磁感应强度:
- (1) 两导体之间;
- (2) 外导体以外;
- (3) 外导体中。
颞 6.25图
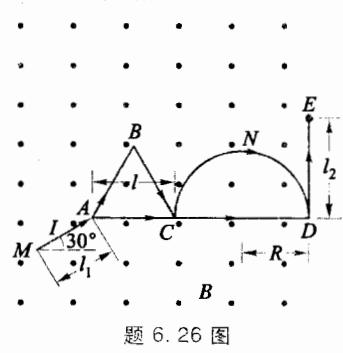
6.26 如图所示,在均匀磁场 B 中,在垂直于 B 的平面上放置电阻率较大的导线构件,从端点输入总电流 I,求 MA、等边三角形 ABC、半圆形 CND、及直线 CD、DE 各部分所受安培力。
6.27 一半径为 4 cm 的圆环,放在非均匀磁场中,环上各处磁场方向对环而言是对称发散的,如图所示,圆环所在处的磁感应强度大小是 0.1 T,磁场方向和环面法向成 60°角,当圆环上电流为 15.8 A 时,求圆环所受合力的大小和方向。
-
- 28 半径为 15. 2 cm 的平面线圈 N=100 匝,通有电流 I=6. 28 A,求带电线圈的磁矩是多少?
- 6.29 截面积为 S,密度为 ρ 的铜质直导线,其中 一段被折成边长为 l 的正方形的三个边,如图所示,可
绕水平轴转动,导线放在方向为竖直向上的匀强磁场中,当导线中的电流为 I 时,导线偏离原来的竖直位置而转一角度 后平衡,求磁感应强度 。
6.30 电流计线圈长 4.00 cm, 宽为 2.00 cm, 共600 匝, 有强度为 10-6 A 的电流通过, 设磁感应强度大小为 0.05 T, 线圈法线与磁场垂直, 试求线圈所受力矩。
6.31 如图所示,在一个通有电流 I 的闭合回路 abcda 中,ab 是一段可滑动的导体,长度为 l,回路平面 与一磁感应强度为 B 的均匀磁场垂直,若保持电流不变,试证当 ab 向右滑动 时,安培力 F 所做的功为 为通过回路的磁通量变化)。
6.32 设一载流线圈在勾强磁场内转动,若保持线圈中的电流 I 不变,试证,当线圈在安培力作用下转过角度 时,磁力所做的功为 ( 为穿过线圈的磁通量的变化)。
6.33 如图所示,有宽度为 a 的无限长薄导体板,均匀流过电流 I,现将其折成直角,现有一带电荷量为-q,速度为 k 的粒子通过 P点,求粒子动量变化的速率 P点距 O点为 d+a。
题 6.33图
- 6.34 已知电子电荷量 e=1.6×10-19 C,当电子进 人 B=800 G 的磁场中时,具有速度为 1.2×107 m·s-1, 方向与磁感应线夹角分别为(1)30°,(2)60°,(3)90°。 求各种情况下,电子所受的洛伦兹力。
- 6.35 如图所示,一束氯原子的同位素离子(它是含有质量为35 u和37 u的混合物,而1 u=1.67× kg)垂直进人 B=0.5 T的磁场,所有离子具有2.0× m·s-1的相同速率,在磁场中偏转180°后,这些离子打在照相底片上,试求离子束在底片上分离开的距离。
题 6.35 图
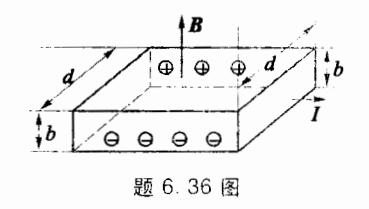
6.36 横截面 m2 的带状银质导线,通有电流 5 A,有 1 T 的磁场垂直于横截面,如图所示。求霍尔电动势。(银的密度 g·cm-3,银的摩尔质量为 M=0.108 kg·mol-1。)
- 6.37 一细铁环的中心线周长为 36 cm, 横截面积为 0.8 cm², 在环上绕有N=400 匝线圈, 当线圈中通过 I=24 mA 的电流时, 通过截面的磁通量 Wb。求环内 B、H、M 的大小及铁环的磁化率 和相对磁导率 。
- 6.38 铝的相对磁导率 ,铜的相对磁导率 ,试求它们的磁化率 并指出它们属于哪种磁介质。
- 6.39 一根沿轴向均匀磁化的棒,直径为 25 mm, 长为 75 mm, 磁矩为12 000 。求棒的磁化强度大小 M 及侧面上的分子电流面密度 。
-
- 40 在一个原子内,原子核的电荷量为 Ze,试求当一个电子绕核半径为r的圆形轨道上运动时的轨道磁矩 为原子核中的质子数)。
- 6.41 某截面为矩形的螺绕环,其平均周长为 0.1 m,横截面积为 0.5×10-4 m2,线圈匝数为 N=200 匝,当通过电流 I=0.1 A 时,测得穿过矩形横截面的 磁通量 Wb。计算该螺绕环所填充的磁介质的相对磁导率。
- 6.42 一根磁棒,体积为 ,磁矩为 ,棒内 ,求棒内的磁场强度。