6.1 恒定电流

6.1.1 电流密度

文档:奥斯特

文档:安培

文档:电流的描述

电流形成需要两个条件:① 存在可以自由移动的电荷;② 驱动电荷做定向移动的力。固态金属中的电子、电解质溶液中的离子等都是可以自由移动的电荷。将含有大量可以自由运动电荷的物体统称为导体。本章主要以固态金属导体为例讲解。

在导体中驱动电荷做定向运动的力,有静电力和非静电力。 将导体放入电场中,导体中的电荷会在电场力的作用下定向移动,电荷的这种定向移动就形成了电流。只要保持导体中有电场 存在,或者有某种相当于电场的非静电力存在,电流就能维持 下去。

不妨设想导体中存在一个电场 E,则每个电荷所受电场力为 F=qE。受力电荷本应产生加速度,但是,由于它们不可避免地要与导体中其他带电粒子或构成固态金属框架的晶体晶格作非完全弹性碰撞,碰撞使它们失去了部分能量或改变运动方向,因此电荷本身只能得到属于每个运动电荷的平均速度,这个速度称为定向漂移速度,以 $v_a$ 表示。如果做定向漂移的是带负电荷的电子,则 $v_a$ 与导体中电场的方向相反。导体晶格因碰撞而获得能量,使绝热条件下导体的温度升高。

定量描述实物电流大小的物理量叫作电流,用 I 表示。如图

6-1 所示,设想在导体内任取一小截面 $\Delta S$ ,如果在时间 $\Delta t$ 内由该截面的某侧向另一侧漂移的电荷量为 $\Delta q$ ,则电流的定义为

$$I = \lim_{\Delta t \to 0} \frac{\Delta q}{\Delta t} = \frac{\mathrm{d}q}{\mathrm{d}t}$$

(6.1.1)

电流的单位是 $A(1 A=1 C \cdot s^{-1})$ 。电流是一个标量,但是有正、负之分,规定正电荷定向漂移的方向为电流的方向。

当电流通过不同形状的导体时,电流虽能给出通过某截面上电流整体的性质,但在不同截面处的电流大小与方向并不一定相同。为了更好地描述导体内部电荷分布及流动的情况,引入电流密度 J。

如图 6-2 所示,在导体内某点附近作一垂直于电荷运动方向的小面元 $dS_{\perp}$ ,而通过该小面元的电流为 dI,则定义电流密度 J的大小为单位时间内垂直穿过单位面积的电荷量或垂直穿过单位面积的电流,其大小

$$J = \frac{\mathrm{d}I}{\mathrm{d}S_{\perp}} \tag{6.1.2}$$

式(6.1.2)还可以写成为

$$dI = JdS_{\perp} \tag{6.1.3}$$

当所选面元与电荷移动方向不垂直,彼此间夹角为 $\theta$ 时,可将该面元在垂直于电荷运动的方向作投影,如图6-2所示,从而得到 $dS_{\perp}=dS\cos\theta$ 。于是式(6.1.3)可以表示为

$$dI = J\cos\theta dS = J \cdot dS \quad \text{id} \quad J = \frac{dI}{dS_{\perp}} e_n \qquad (6.1.4)$$

式中, $e_n$ 代表 d $S_\perp$ 的单位法线矢量。

对于通过导体某任意曲面 S 上的电流,只需将式(6.1.4)对该曲面积分,即

$$I = \int_{S} \mathbf{J} \cdot d\mathbf{S} \tag{6.1.5}$$

电流密度 J 是一个矢量,它反映出导体内某点处正电荷运动的方向,对金属导体而言,也是该点附近电场强度的方向。随后我们将看到导体内某点(局域)处,电流密度的大小与该点(局域)处电场强度的大小成正比例关系。

电流密度 J 在导体中的分布也可以用一组有方向的曲线来描述,这组曲线叫作电流线。电流线的疏密表示电流大小的分布,电流线上任意点的切线方向,表示正电荷在该点处的漂移方向。在国际单位制中,电流密度的单位是 A·m^-2(安培每平方米)。

下面分析导体内某个小局域的电流密度与该局域处正电荷

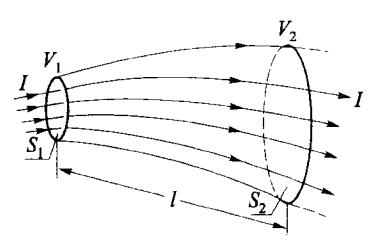
图 6-1 电流

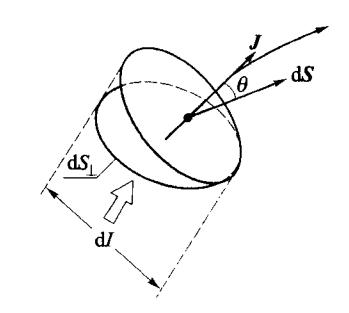
图 6-2 电流密度和电流的关系

图 6-3 电流密度与电荷的关系

漂移速度间的关系。

如图 6-3 所示,在导体内某点 P 的邻域内沿电流线方向作一小柱体,小柱体的端面积为 dS 并与电流线垂直。小柱体的长为 $v_a dt$ ,正电荷的密度为 n,每个电荷所带电荷量为 q,则在时间 dt 内通过 dS 面的总电荷量 $dQ = dSv_a dtnq$ ,即通过 dS 面的电流 $dI = \frac{dQ}{dt} = v_a nq dS$ 。依式(6.1.4),得出电流密度为

$$\boldsymbol{J} = \frac{\mathrm{d}\boldsymbol{I}}{\mathrm{d}\boldsymbol{S}} \boldsymbol{e}_{\mathrm{n}} = \boldsymbol{v}_{\mathrm{d}} \boldsymbol{n} \boldsymbol{q}$$

上式说明,如果金属中形成电流真的是正电荷的话,那么,J 应与正电荷的运动方向相同。但是,实际上金属导体中形成电流 的是自由电子,自由电子带负电,考虑到自由电子定向漂移所形 成的电流与等量的正电荷以同速率沿相反方向漂移形成电流的 对外效应几乎等效,为了简单起见,在此,将电流视为正电荷运动 的结果。而对于自由电子来说,电流密度 J 与自由电子的定向漂 移速度 v_a 的关系为

$$\boldsymbol{J} = -en \boldsymbol{v}_d$$

式中,e 为电子电荷量,n 为自由电子的密度。

6.1.2 电流的连续性方程及恒定电流

仿照静电场中高斯定理,可在有电流密度的空间作一高斯面S,并仍然规定S 面的外法线方向为正向。根据电荷守恒定律,从S 面内流出的电流 $\oint_S \boldsymbol{J} \cdot d\boldsymbol{S}$ 应等于S 面所围体积V 内电荷量的减少率 $-\frac{dq}{dt}$ ,即

$$\oint_{S} \mathbf{J} \cdot d\mathbf{S} = -\frac{dq}{dt}$$

(6.1.5a)

若 V 中电荷为连续分布, $q = \int_{\Gamma} \rho_e dV$ ,则上式为

$$\oint_{S} \mathbf{J} \cdot d\mathbf{S} = -\int_{V} \frac{\partial \rho_{e}}{\partial t} dV \qquad (6.1.5b)$$

式中, $\rho_e$ 表示电荷体密度, $\frac{\partial \rho_e}{\partial t}$ 表示电荷体密度对时间的变化率。 利用数学中的高斯公式得

$$\nabla \cdot \boldsymbol{J} = -\frac{\partial \rho_{e}}{\partial t} \tag{6.1.6}$$

式中, $\nabla \cdot J$ 称为J的散度,是式(6.1.5b)的微分形式。其物理意义是:在一个微小的局域内,若J的散度不为零,则该局域内一定有电荷在随着时间增加或减少。

式(6.1.5)和式(6.1.6)均为电荷守恒定律在电流场中的表达形式,分别称为电流的连续性方程的积分和微分形式。

如果在电场中任意闭合面 S 上,流入曲面 S 的电流等于流出曲面的电流,则称这种电流为恒定电流,恒定电流的条件有积分形式和微分形式两种,其积分形式为

$$\oint_{S} \mathbf{J} \cdot d\mathbf{S} = -\frac{dq}{dt} = 0 \quad \text{in} \quad \oint_{S} \mathbf{J} \cdot d\mathbf{S} = -\oint_{V} \frac{\partial \rho_{e}}{\partial t} dV = 0$$

(6.1.7)

它表明在恒定电流场中任意闭合面 S 内的电荷不随时间变化(即 $\frac{dq}{dt}$ =0)。与式(6.1.7)相对应的微分形式为

$$\nabla \cdot \boldsymbol{J} = 0 \tag{6.1.8}$$

此式称为恒定电流条件的微分形式,表明电流场中任何点邻域 内的电荷体密度不随时间变化(即 $\frac{\partial \rho_e}{\partial t}$ =0)时,电流即为恒定电流。

电荷不随时间变化意味着电场也不随时间变化,因此,在恒 定电流中电场是不随时间变化的。

6.1.3 欧姆定律的微分形式

1826年,德国科学家欧姆通过实验发现,当保持导线温度不变时,改变加在一段导线上的电压,导线内的电流也随之变化,并且与外电压成正比,这就是欧姆定律,公式写为

$$I = U/R \quad \text{if} \quad U = RI \tag{6.1.9}$$

式中,R 为比例系数,称为导体的电阻,单位是 $\Omega$ (欧姆)。其倒数1/R 称为电导,用G 表示,G=1/R,单位是S(西门子)。

导体电阻与材料性质、导体形状及温度有关。实验表明,在温度不变的情况下,对一段均匀圆柱体而言,电阻的大小与其长度 l 成正比,与其截面积 S 成反比,即

$$R = \rho(l/S)$$

式中, $\rho$ 为比例系数,称为电阻率,其单位是 $\Omega$ ·m(欧姆米),其大小与导体性质及温度有关。

式(6.1.9)是欧姆定律的宏观表现形式,可以通过仪器直接

图 6-4 欧姆定律微分形式的推导

测量。但要知道导体内某点邻域处电流密度 J 和恒定电场 E 的 关系,就要应用欧姆定律的微分形式。

如图 6-4 所示,在导体某点 P 的邻域处,沿电流线方向取长为 $\Delta l$ ,截面积为 $\Delta S$ 的小柱体。由于柱体两端的截面都与电流线垂直,即都与电场线垂直,所以小柱体的两端分别为等势面,小柱体内电场强度 E 和电流密度的关系都可视为不变,流经截面的电流 $\Delta I = J\Delta S$ ,小柱体两端电压为 $\Delta U = E\Delta l$ ,电阻 $R = \rho(\Delta l/\Delta S)$ ,利用式 (6.1.9) 有 $J = E/\rho$ ,改写为 $J = \sigma E$ 。式中, $\sigma = 1/\rho$ 称为电导率,单位是 $S \cdot m^{-1}$ (西门子每米)。在不存在其他非静电力的各向同性导体中,J 和 E 的方向是逐点相同的,所以,可以写成矢量方程

$$\mathbf{J} = \boldsymbol{\sigma} \mathbf{E} \tag{6.1.10}$$

这就是欧姆定律的微分形式,它说明了J和E数值与方向的关系。