NOTE
热力学研究各种过程的目的之一,就是探索如何提高热机的效率。所谓热机,是指通过工作物质(简称工质)不断把吸收的热量转化为机械功的装置,如蒸汽机、内燃机、汽轮机等。热机中工作物质所进行的过程是循环过程。
4.4.1 循环过程及其效率
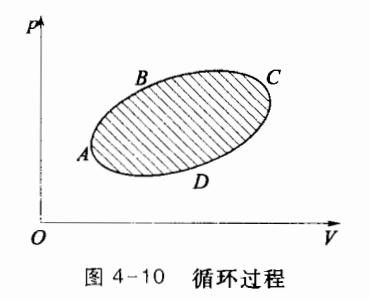
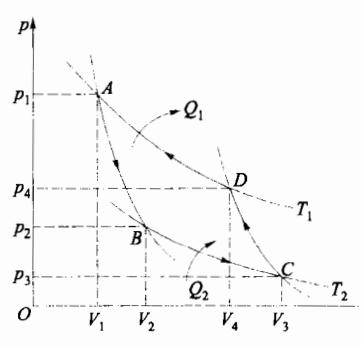
若一个系统从某一状态出发,经过一系列状态变化后,又恢复到原来的状态,这样的过程称为循环过程。如图 4-10 所示,闭合曲线 ABCDA 为某一准静态循环过程曲线。系统经历一次循环过程后,其内能的变化 Δ E = 0 \Delta E=0 Δ E = 0
循环过程有两种,在 p-V 图中,如果循环过程是沿顺时针方向进行的,称为正循环;反之称为逆循环。对于正循环,如图 4-10 所示,系统由状态 A 开始,经状态 B 到达状态 C,系统对外做正功,其值为 ABC 曲线与 V 轴所围面积。而当系统从状态 C 出发,经 D 返回到初态 A 的过程中,系统做负功,数值等于 CDA 曲线与 V 轴所围面积。在整个循环过程中,系统对外做的总功(净功)为上述二阶段中做功的代数和,可见,在正循环中,系统对外做的总功为正,并且,在数值上等于闭合曲线 ABCDA 所包围的面积。热机中工作物质所进行的循环就是正循环。
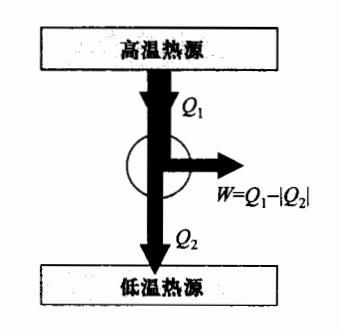
在热机中,工质将从高温热源吸收的热量,部分用来对外做功,部分释放到低温热源,最终回到初始状态。热机在一个循环过程中能量的转化情况如图 4-11 所示, Q 1 Q_1 Q 1 Q 2 Q_2 Q 2 Δ E = 0 \Delta E=0 Δ E = 0
Q 1 + Q 2 = W ( 4.4.1 ) Q_1 + Q_2 = W (4.4.1) Q 1 + Q 2 = W ( 4.4.1 ) 或
Q 1 − ∣ Q 2 ∣ = W ( 4.4.2 ) Q_1 - |Q_2| = W (4.4.2) Q 1 − ∣ Q 2 ∣ = W ( 4.4.2 ) 这表明,在循环过程中,系统对外所做的净功等于系统吸收的 净热。
为表明热机把吸收的热量转化为做功的能力,将工质在一次
图 4-11 热机循环过程能量图
循环过程中对外做的功 W 与所吸热量 Q 1 Q_1 Q 1 η \eta η
η = W Q 1 = Q 1 − ∣ Q 2 ∣ Q 1 = 1 − ∣ Q 2 ∣ Q 1 \eta = \frac{W}{Q_1} = \frac{Q_1 - |Q_2|}{Q_1} = 1 - \frac{|Q_2|}{Q_1} η = Q 1 W = Q 1 Q 1 − ∣ Q 2 ∣ = 1 − Q 1 ∣ Q 2 ∣ (4.4.3)
可以看出,当吸收热量 Q 1 Q_1 Q 1 ∣ Q 2 ∣ |Q_2| ∣ Q 2 ∣
例题 4-4
1 mol 氧气(视为刚性双原子分子理想气体)做如图 4-12 所示的循环,其中 AB 为直线,BC 为绝热线,CA 为等温线,并已知 θ \theta θ T 1 T_1 T 1 T 2 T_2 T 2 T 1 T_1 T 1 V 3 V_3 V 3 V 1 V_1 V 1 R 2 R_2 R 2
(1) 各过程中气体做功、吸收热量及内能增量;
(2) 循环效率。
图 4-12 例题 4-4图
M : ( 1 ) A → B M:(1) A \rightarrow B M : ( 1 ) A → B 直线过程:
W 12 = ( p 1 + p 2 ) ( V 2 − V 1 ) 2 W_{12} = \frac{(p_1 + p_2) (V_2 - V_1)}{2} W 12 = 2 ( p 1 + p 2 ) ( V 2 − V 1 ) = p 1 V 2 + p 2 V 2 − p 1 V 1 − p 2 V 1 2 = \frac{p_1 V_2 + p_2 V_2 - p_1 V_1 - p_2 V_1}{2} = 2 p 1 V 2 + p 2 V 2 − p 1 V 1 − p 2 V 1 由图可知
P 1 V 1 = P 2 V 2 \frac{P_1}{V_1} = \frac{P_2}{V_2} V 1 P 1 = V 2 P 2 Q ⃗ \vec{Q} Q Q ⃗ \vec{Q} Q Q ⃗ \vec{Q} Q Q ⃗ \vec{Q} Q
所以有
W 12 = p 2 V 2 − p 1 V 1 2 = 1 2 R ( T 2 − T 1 ) W_{12} = \frac{p_2 V_2 - p_1 V_1}{2} = \frac{1}{2} R (T_2 - T_1) W 12 = 2 p 2 V 2 − p 1 V 1 = 2 1 R ( T 2 − T 1 ) = 1 2 × 8.314 × ( 600 − 300 ) J = 1 247 J = \frac{1}{2} \times 8.314 \times (600 - 300) \text{ J} = 1 \text{ }247 \text{ J} = 2 1 × 8.314 × ( 600 − 300 ) J = 1 247 J 内能增量为
Δ E 12 = C V , m ( T 2 − T 1 ) = 5 2 R ( T 2 − T 1 ) \Delta E_{12} = C_{V, \text{m}} (T_2 - T_1) = \frac{5}{2} R (T_2 - T_1) Δ E 12 = C V , m ( T 2 − T 1 ) = 2 5 R ( T 2 − T 1 ) = 5 2 × 8.314 × ( 600 − 300 ) J = 6 236 J = \frac{5}{2} \times 8.314 \times (600 - 300) \text{ J} = 6 \, 236 \text{ J} = 2 5 × 8.314 × ( 600 − 300 ) J = 6 236 J 吸收热量为
Q 12 = Δ E 12 + W 12 = 7483 Q_{12} = \Delta E_{12} + W_{12} = 7483 Q 12 = Δ E 12 + W 12 = 7483 J B → C B \rightarrow C B → C
Q 23 = 0 Q_{23} = 0 Q 23 = 0 Δ E 23 = C V , m ( T 3 − T 2 ) = 5 2 R ( T 1 − T 2 ) \Delta E_{23} = C_{V,\text{m}} (T_3 - T_2) = \frac{5}{2} R (T_1 - T_2) Δ E 23 = C V , m ( T 3 − T 2 ) = 2 5 R ( T 1 − T 2 ) = 5 2 × 8.314 × ( 300 − 600 ) J = − 6 236 J = \frac{5}{2} \times 8.314 \times (300 - 600) \text{ J} = -6\,236 \text{ J} = 2 5 × 8.314 × ( 300 − 600 ) J = − 6 236 J W 23 = − Δ E 23 = 6 236 J W_{23} = -\Delta E_{23} = 6 \ 236 \ J W 23 = − Δ E 23 = 6 236 J C → A C \rightarrow A C → A
Δ E 31 = 0 \Delta E_{31} = 0 Δ E 31 = 0 W 31 = Q 31 = R T 1 ln V 1 V 3 = 8.314 × 300 × ln 1 8 J W_{31} = Q_{31} = RT_1 \ln \frac{V_1}{V_3} = 8.314 \times 300 \times \ln \frac{1}{8} \text{ J} W 31 = Q 31 = R T 1 ln V 3 V 1 = 8.314 × 300 × ln 8 1 J = -5 187 J
(2) 循环效率为
η = 1 − ∣ Q 2 ∣ Q 1 = 1 − 5 187 7 483 = 30.7 % \eta = 1 - \frac{|Q_2|}{Q_1} = 1 - \frac{5 \ 187}{7 \ 483} = 30.7\% η = 1 − Q 1 ∣ Q 2 ∣ = 1 − 7 483 5 187 = 30.7% 或用净功与吸收热量之比求出,即
η = W 74 Q 1 = 1247 + 6236 − 5187 7483 = 30.7 % \eta = \frac{W_{74}}{Q_1} = \frac{1247 + 6236 - 5187}{7483} = 30.7\% η = Q 1 W 74 = 7483 1247 + 6236 − 5187 = 30.7% 例题 4-5
一定量的刚性双原子分子理想气体进行如图 4-13 所示的循环。已知状态 A 的温度为 300 K。求:(1)状态 B 和状态 C 的温度;(2)各阶段吸收的热量。
解:(1) 由 p A V A T A = p B V B T B = p C V C T C \frac{p_A V_A}{T_A} = \frac{p_B V_B}{T_B} = \frac{p_C V_C}{T_C} T A p A V A = T B p B V B = T C p C V C T B = 225 K T_B = 225\text{ K} T B = 225 K
和 T C = 75 K T_C = 75\text{ K} T C = 75 K
(2) CA 过程吸收的热量:
Q C A = m M C V , m ( T A − T C ) = 5 2 m M R ( T A − T C ) Q_{CA} = \frac{m}{M} C_{V, m} (T_A - T_C) = \frac{5}{2} \frac{m}{M} R (T_A - T_C) Q C A = M m C V , m ( T A − T C ) = 2 5 M m R ( T A − T C ) = 5 2 ( p A V A − p C V C ) = \frac{5}{2} (p_A V_A - p_C V_C) = 2 5 ( p A V A − p C V C ) = 5 2 × ( 400 × 2 − 100 × 2 ) J = 1500 J = \frac{5}{2} \times (400 \times 2 - 100 \times 2) \text{ J} = 1500 \text{ J} = 2 5 × ( 400 × 2 − 100 × 2 ) J = 1500 J BC 过程吸收的热量:
Q B C = m M C p , m ( T C − T B ) = 7 2 m M R ( T C − T B ) = 7 2 ( p C V C − p B V B ) = 7 2 × ( 100 × 2 − 100 × 6 ) J = − 1400 J Q_{BC} = \frac{m}{M} C_{p, m} (T_C - T_B) = \frac{7}{2} \frac{m}{M} R (T_C - T_B) \\ = \frac{7}{2} (p_C V_C - p_B V_B) \\ = \frac{7}{2} \times (100 \times 2 - 100 \times 6) \text{ J} = -1400 \text{ J} Q BC = M m C p , m ( T C − T B ) = 2 7 M m R ( T C − T B ) = 2 7 ( p C V C − p B V B ) = 2 7 × ( 100 × 2 − 100 × 6 ) J = − 1400 J AB 过程吸收的热量:
400
程中吸收的 图 4-13 例题 4-5 图 净热量减去
CA 过程和 BC 过程中吸收的热量,而循环过程中吸收的净热量等于净做功,即
Q A B = Q A B − ( Q C A + Q B C ) = W A B − ( Q C A + Q B C ) Q_{AB} = Q_{AB} - (Q_{CA} + Q_{BC}) = W_{AB} - (Q_{CA} + Q_{BC}) Q A B = Q A B − ( Q C A + Q BC ) = W A B − ( Q C A + Q BC ) W 净 = ( p A − p C ) ( V B − V C ) 2 W_{\text{净}} = \frac{(p_A - p_C)(V_B - V_C)}{2} W 净 = 2 ( p A − p C ) ( V B − V C ) = ( 400 − 100 ) × ( 6 − 2 ) 2 J = 600 J = \frac{(400 - 100) \times (6 - 2)}{2} \text{ J} = 600 \text{ J} = 2 ( 400 − 100 ) × ( 6 − 2 ) J = 600 J 所以
Q A B = 500 J Q_{AB} = 500 \text{ J} Q A B = 500 J 可见,在 CA 和 AB 过程系统吸热,在 BC 过程系统放热。
4.4.2 卡诺循环
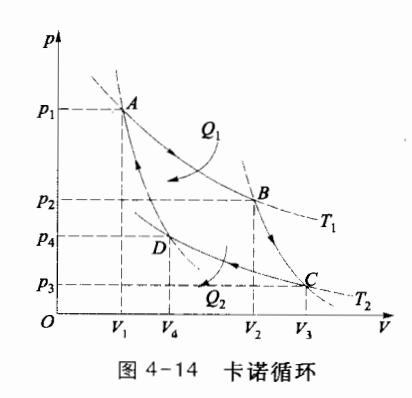
18世纪末到 19世纪初,蒸汽机在工业上的应用越来越广泛,但当时蒸汽机的效率很低,只有 3%5%,有超过 95%的能量未被利用。因此,如何提高热机效率,成为当时许多科学家和工程师孜孜以求的问题。1824年,法国青年工程师卡诺(Sadi Carnot)提出了一种理想热机,称为卡诺热机,其中工作物质的循环过程,称为卡诺循环,它由两个等温过程和两个绝热过程构成,所有过程都是准静态的,如图 414 所示。在整个循环过程中,卡诺热机的工质只与两个恒温热源交换热量,在温度为 T,的高温
热源吸热,在另一温度为T。的低温热源放热。
下面,分析以理想气体作为工作物质的卡诺循环的效率。在循环过程中,工质从高温热源 T1 吸收的热量为
Q 1 = m M R T 1 ln V 2 V 1 Q_1 = \frac{m}{M} R T_1 \ln \frac{V_2}{V_1} Q 1 = M m R T 1 ln V 1 V 2 (4.4.4)
向低温热源 T,放出的热量为
∣ Q 2 ∣ = m M R T 2 ln V 3 V 4 |Q_2| = \frac{m}{M}RT_2 \ln \frac{V_3}{V_4} ∣ Q 2 ∣ = M m R T 2 ln V 4 V 3 (4.4.5)
根据热机效率的定义
η = 1 − ∣ Q 2 ∣ Q 1 = 1 − m M R T 2 ln V 3 V 4 m M R T 1 ln V 2 V 1 = 1 − T 2 ln V 3 V 4 T 1 ln V 2 V 1 \eta = 1 - \frac{|Q_2|}{Q_1} = 1 - \frac{\frac{m}{M}RT_2\ln\frac{V_3}{V_4}}{\frac{m}{M}RT_1\ln\frac{V_2}{V_1}} = 1 - \frac{T_2\ln\frac{V_3}{V_4}}{T_1\ln\frac{V_2}{V_1}} η = 1 − Q 1 ∣ Q 2 ∣ = 1 − M m R T 1 ln V 1 V 2 M m R T 2 ln V 4 V 3 = 1 − T 1 ln V 1 V 2 T 2 ln V 4 V 3 (4. 4. 6)
BC 和 DA 是两个绝热过程,有
T 1 V 2 γ − 1 = T 2 V 3 γ − 1 T_1 V_2^{\gamma-1} = T_2 V_3^{\gamma-1} T 1 V 2 γ − 1 = T 2 V 3 γ − 1 及
T 1 V 1 γ − 1 = T 2 V 4 γ − 1 T_{1}V_{1}^{\gamma-1} = T_{2}V_{4}^{\gamma-1} T 1 V 1 γ − 1 = T 2 V 4 γ − 1 二式相除,得 ( V 2 V 1 ) γ − 1 = ( V 3 V 4 ) γ − 1 \left(\frac{V_{2}}{V_{1}}\right)^{\gamma-1} = \left(\frac{V_{3}}{V_{4}}\right)^{\gamma-1} ( V 1 V 2 ) γ − 1 = ( V 4 V 3 ) γ − 1 V 2 V 1 = V 3 V 4 \frac{V_{2}}{V_{1}} = \frac{V_{3}}{V_{4}} V 1 V 2 = V 4 V 3
η 卡 = 1 − T 2 T 1 ( 4.4.7 ) \eta_{\text{卡}} = 1 - \frac{T_{2}}{T_{1}} \quad (4.4.7) η 卡 = 1 − T 1 T 2 ( 4.4.7 ) 可见,卡诺循环的效率只决定于高温热源与低温热源的绝对 温度,与工作物质无关。
4.4.3 制冷机的工作过程
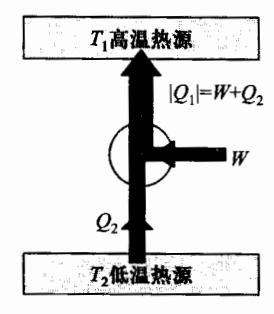
逆循环过程在 p-V 图中是沿逆时针方向进行的,制冷机中的工质所进行的就是逆循环过程。逆循环过程又称为制冷循环。如图 4-10 所示,对于逆循环,系统在 CBA 过程中对外做负功,或外界对系统做功,在 ADC 过程系统对外做正功。整个循环中,系统对外所做总功为负,即外界对系统做正功,循环曲线所围面积的值等于外界对系统所做的总功 W。在逆循环中,系统从低温热源吸收热量 Q 2 Q_2 Q 2 ∣ Q 1 ∣ |Q_1| ∣ Q 1 ∣
图 4-15 制冷机循环过程能量图
图 4-16 卡诺制冷循环
形如图 4-15 所示。
制冷机的制冷性能用制冷系数反映,定义为在一次逆循环过程中系统从低温热源吸收的热量 Q 2 Q_2 Q 2 ε \varepsilon ε
ε = Q 2 W = Q 2 ∣ Q 1 ∣ − Q 2 (4.4.8) \varepsilon = \frac{Q_2}{W} = \frac{Q_2}{|Q_1| - Q_2} \tag{4.4.8} ε = W Q 2 = ∣ Q 1 ∣ − Q 2 Q 2 ( 4.4.8 ) 图 4-16 是以理想气体为工作物质的卡诺制冷机的循环图,显然卡诺制冷机的制冷系数为
ε ± = T 2 T 1 − T 2 (4.4.9) \varepsilon_{\pm} = \frac{T_2}{T_1 - T_2} \tag{4.4.9} ε ± = T 1 − T 2 T 2 ( 4.4.9 ) 例题 4-6
有一卡诺热机,每一循环过程中从温度为 T 1 T_1 T 1 Q 1 Q_1 Q 1 4 J, 并向温度为 T 2 T_2 T 2
(1) 求循环的效率和每一循环中系统所做净功;
(2) 如将高温热源的温度提高到 T 1 ′ = 600 K T_1' = 600 \text{ K} T 1 ′ = 600 K
解:(1)卡诺循环效率为
η = 1 − T 2 T 1 = 1 − 300 400 = 25 % \eta = 1 - \frac{T_2}{T_1} = 1 - \frac{300}{400} = 25\% η = 1 − T 1 T 2 = 1 − 400 300 = 25% 循环中系统所做净功为
W = η Q 1 = 0.25 × 2.4 × 10 4 J = 6000 J W = \eta Q_1 = 0.25 \times 2.4 \times 10^4 \text{ J} = 6000 \text{ J} W = η Q 1 = 0.25 × 2.4 × 1 0 4 J = 6000 J (2) 高温热源温度提高后的效率为
η ′ = 1 − T 2 T 1 ′ = 1 − 300 600 = 50 % \eta' = 1 - \frac{T_2}{T_1'} = 1 - \frac{300}{600} = 50\% η ′ = 1 − T 1 ′ T 2 = 1 − 600 300 = 50% 净功为
W ′ = η ′ Q 1 = 0.5 × 2.4 × 10 4 J = 1.2 × 10 4 J W' = \eta' Q_1 = 0.5 \times 2.4 \times 10^4 \text{ J} = 1.2 \times 10^4 \text{ J} W ′ = η ′ Q 1 = 0.5 × 2.4 × 1 0 4 J = 1.2 × 1 0 4 J
例题 4-7
若用一卡诺制冷机使 1 kg 的 0 ∘ ^{\circ} ∘ ∘ ^{\circ} ∘ ∘ ^{\circ} ∘ ∘ ^{\circ} ∘ − 1 ^{-1} − 1
解:该卡诺制冷机的制冷系数为
ε = Q 2 W = T 2 T 1 − T 2 = 273 300 − 273 = 273 27 \varepsilon = \frac{Q_2}{W} = \frac{T_2}{T_1 - T_2} = \frac{273}{300 - 273} = \frac{273}{27} ε = W Q 2 = T 1 − T 2 T 2 = 300 − 273 273 = 27 273 使 1 kg 的 0 ℃的水变成 0 ℃的冰需提供的 热量为
Q 1 = 33.47 × 10 4 × 1 J = 33.47 × 10 4 J Q_1 = 33.47 \times 10^4 \times 1 \text{ J} = 33.47 \times 10^4 \text{ J} Q 1 = 33.47 × 1 0 4 × 1 J = 33.47 × 1 0 4 J 需要的功为
W = Q 2 ϵ = 27 273 × 33.47 × 10 4 J = 3.31 × 10 4 J W = \frac{Q_2}{\epsilon} = \frac{27}{273} \times 33.47 \times 10^4 \text{ J} = 3.31 \times 10^4 \text{ J} W = ϵ Q 2 = 273 27 × 33.47 × 1 0 4 J = 3.31 × 1 0 4 J 释放的热量为
Q = W + Q 2 = ( 3.31 + 33.47 ) × 10 4 J Q = W + Q_2 = (3.31 + 33.47) \times 10^4 \text{ J} Q = W + Q 2 = ( 3.31 + 33.47 ) × 1 0 4 J = 36.8×104 J
4.5 热力学第二定律 _
4.5.1 热力学第二定律的表述
热力学第二定律是人们在研究如何提高热机与制冷机的工作效能的问题中总结出来的,它是独立于热力学第一定律的另一热力学基本定律。利用热力学第二定律,可以对与热现象有关的过程的进行方向加以判断。
由热机效率的定义式 η = 1 − ∣ Q 2 ∣ Q 1 \eta=1-\frac{|Q_2|}{Q_1} η = 1 − Q 1 ∣ Q 2 ∣
只需将从高温热源吸收的热量 Q 1 Q_1 Q 1 Q 2 Q_2 Q 2 Q 2 Q_2 Q 2
不可能从单一热源吸收热量,使之完全转化为功,而不产生 其他影响。
这里所说的"其他影响"指除了吸热做功之外的其他变化。 其实将热量完全转化为功,是可以做到的,例如理想气体在等温 膨胀过程中就把吸收的热量完全转化为功,但在这一过程中,理 想气体的体积增加了,即产生了其他影响。
人们把从单一热源吸收的热量完全用来对外做功的热机(即效率为100%的热机)称为第二类永动机。热力学第二定律告诉我们,第二类永动机是不可能制成的。
由制冷机制冷系数的定义式 ε = Q 2 W \varepsilon = \frac{Q_2}{W} ε = W Q 2
不可能把热量从低温物体传到高温物体,而不产生其他 影响。
文档: 热力学第二定律
NOTE
When you are face to face with a difficulty, you are up against a discovery. (Lord Kelvin)
克劳修斯表述是指在没有其他影响的前提下,是不可能将热量从低温物体传到高温物体的。若存在其他影响,热量从低温物体向高温物体传递是可以的,这正是制冷机工作过程的特点。在制冷机的工作过程中,热量不是自发传递的,它依赖了外界对系统做功,引起了周围环境状态的改变。
开尔文表述中所涉及的功转化为热和热转化为功的过程是一对对应的热力学过程。同样,热量由高温物体向低温物体传递和热量由低温物体向高温物体传递的过程同样是一对对应的热力学过程。由以上讨论知,功变热与热量由高温物体传向低温物体的过程,二者宏观表现上有共同之处,即二者都是自发的,或自动的,无条件发生的;而与之相反的过程则不是自发的,需要一定条件或限制才能发生。实际上,一切实际的热力学过程都是按一定方向进行的,相反的热力学过程虽然符合热力学第一定律,但不可能自动发生。可见,热力学第二定律是关于自然过程方向的规律,阐明了宏观热力学过程具有方向性。
4.5.2
热力学第二定律两种表述的 等效性
从表面上看,热力学第二定律的两种表述似乎彼此无关,开尔文表述针对的是热功转化现象,而克劳修斯表述阐述的是热传导现象,其实从实质上看,二者是完全等效的。下面我们用反证法证明二者的等效性,即若违背了其中一种表述,则另一种表述也不成立,反之亦然。
首先假定开尔文表述不成立,将必然导致克劳修斯表述的不成立。
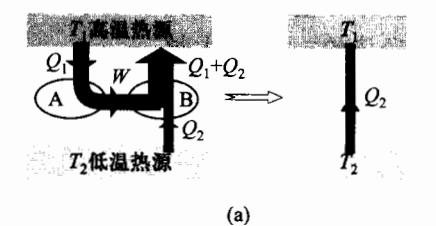
如图 4-17(a) 所示,设有一热机 A,在一个循环中,它能从高温热源 T 1 T_1 T 1 Q 1 Q_1 Q 1 Q 1 = W Q_1 = W Q 1 = W
开尔文表述不成立 ===> 克劳修斯表述不成立
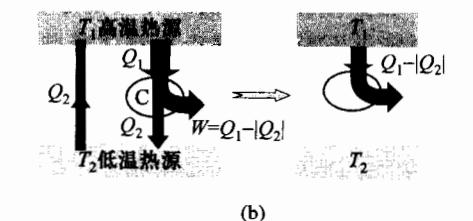
克劳修斯表述不成立 ===> 开尔文表述不成立
图 4-17 两种表述的等效性证明
他影响。现将这部分功用来驱动制冷机 B,使制冷机从低温热源 T 2 T_2 T 2 Q 2 Q_2 Q 2 T 1 T_1 T 1 W + Q 2 = Q 1 + Q 2 W+Q_2=Q_1+Q_2 W + Q 2 = Q 1 + Q 2 Q 2 Q_2 Q 2 T 2 T_2 T 2 T 1 T_1 T 1
其次假定克劳修斯表述不成立,也必然导致开尔文表述的不成立。
如图 4-17(b) 所示,假设一定的热量 ∣ Q 2 ∣ |Q_2| ∣ Q 2 ∣ T 2 T_2 T 2 T 1 T_1 T 1 Q 1 Q_1 Q 1 ∣ Q 2 ∣ |Q_2| ∣ Q 2 ∣ Q 1 Q_1 Q 1 ∣ Q 2 ∣ |Q_2| ∣ Q 2 ∣
4.5.3 可逆过程和不可逆过程
如果一个系统从初态 A 出发,经历一系列过程到达终态 B, 若存在另外的过程使系统从终态 B 返回到初态 A,并且使外界恢 复原状,则原来的过程称为可逆过程;反之,无论运用何种方法都 不能使系统和外界恢复到原有的状态,则原来的过程称为不可逆 过程。
可以看出,热力学第二定律的开尔文表述实际上说明了热功转化过程的不可逆性,而克劳修斯表述则说明热传导过程是不可逆的。
我们知道,功可以转化为热,最典型的例子就是摩擦生热现象。一个物体在水平面内向前滑动,由于摩擦,物体速度逐渐减小,最终静止。过程中,功转化为热量,这是自发进行的。但这种能量形式的逆向转化却不会自动发生。这表明热功转化过程是有方向性的,是不可逆的。
两个不同温度的物体相互接触,热量总是自发地从高温物体 传向低温物体。而相反的过程,即热量自动地从低温物体传向高 温物体,使低温物体的温度更低,高温物体的温度更高,这在实际 上是不可能发生的。这说明,热传导过程是有方向性的,是不可 逆的。
热力学第二定律两种表述的等效性进一步说明,热功转化过程的不可逆性与热传导过程的不可逆性是彼此相关的。其实,在自然界中,存在有大量的不可逆过程,可以说凡是自发进行的各
种宏观过程都是不可逆的,例如气体的自由膨胀过程、扩散过程等。而各种不可逆过程间都是彼此关联的,往往能够从一种过程的不可逆性,反之亦然。
正是因为各种不可逆过程是彼此相关的,因此,可以选用任何一个不可逆过程来阐述热力学第二定律的内容,所以,热力学第二定律可以有许多种不同的表述方式,但所有表述所指出的热力学第二定律的本质不变,即,一切与热现象有关的实际宏观过程都是不可逆的。
仔细分析各种不可逆过程发现,它们具有共同的特征:存在不平衡因素或耗散因素。例如扩散过程是由于粒子数密度的不平衡造成的,热传导过程是由于温度不平衡造成的,自由膨胀过程是由于压强不平衡造成的……只有无摩擦的准静态过程才是可逆过程。这是因为,当过程逆向进行时,可以重现原来过程的所有中间状态,并能消除所有的外界影响。可见,可逆过程只是一种理想模型。尽管如此,对可逆过程的研究仍具有理论和现实意义,它可使人们通过对可逆过程的研究去探寻实际过程的规律。
4.5.4 卡诺定理
卡诺定理是卡诺在研究热机效率的过程中提出来的。在讨论卡诺定理的具体内容之前,我们先就可逆循环与不可逆循环进行说明。如果组成一个循环过程的所有中间过程都是可逆过程,我们说该循环过程就是可逆循环,凡做可逆循环的热机(或制冷机)均称为可逆热机(或可逆制冷机);若一个循环过程中含有不可逆的分过程,则该循环过程就是不可逆的,与之相应的热机(或制冷机)就是不可逆热机(或不可逆制冷机)。
卡诺定理的内容包括两条:
(1) 在相同的高温热源(温度 T 1 T_1 T 1 T 2 T_2 T 2
(2) 在相同的高温热源(温度 T 1 T_1 T 1 T 2 T_2 T 2
由卡诺定理(1)可知,工作在高温热源 T 1 T_1 T 1 T 2 T_2 T 2
η Tigs = 1 − ∣ Q 2 ∣ Q 1 = 1 − T 2 T 1 \eta_{\text{Tigs}} = 1 - \frac{|Q_2|}{Q_1} = 1 - \frac{T_2}{T_1} η Tigs = 1 − Q 1 ∣ Q 2 ∣ = 1 − T 1 T 2 (4.5.1)
而根据卡诺定理(2),对于不可逆热机有
η π < 1 − T 2 T 1 (4.5.2) \eta_{\pi} < 1 - \frac{T_2}{T_1} \tag{4.5.2} η π < 1 − T 1 T 2 ( 4.5.2 ) 卡诺定理从理论上指出了提高热机效率的途径,即提高高温 热源的温度,降低低温热源的温度(在实际中常采用提高高温热 源温度的方法),并使热机尽可能接近可逆热机。