4.3.1 绝热过程
如果系统在整个状态变化过程中始终不与外界交换热量,该过程就是绝热过程。例如被绝热性能良好的材料包裹的系统所进行的过程。如果过程进行得很快,可认为在过程结束之前,系统来不及与外界进行热量交换,该过程也可视为绝热过程。
在绝热过程中,dQ=0,或 Q=0,所以由热力学第一定律有 dW=-dE 和 dE=-dW(或 W=−ΔE 和 ΔE=−W ) (4.3.1) 即系统之所以能够对外做功,完全依靠消耗自身内能;或系统内能的增加量等于外界对系统做的功。
绝热过程不是等值过程,在绝热过程中,理想气体的状态参量 p、V、T均是变量。那么准静态绝热过程的过程方程是什么呢?为了回答这一问题,下面我们研究理想气体在准静态绝热过程中状态参量间的变化关系。
pdV=−MmCV,mdT(4.3.2)
NOTE
把理想气体物态方程等号两边进行微分,得
pdV+Vdp=MmRdT(4.3.3)
将上面两式联立,消去 dT,得
CVm(pdV+Vdp)=−RpdV(4.3.4)
由于 Cν,m=R ,上式可重新写为
Cp,mpdV+CV,mVdp=0
(4.3.5)
上式除以 Cv,m 和 pV,整理后,得
pdp+γVdV=0(4.3.6)
将上式积分,得
所以
pV′=C1(x˚±)(4.3.7)
式中 γ=Cv,mCp,m , 称为气体的热容比。
利用式(4.3.7)与理想气体物态方程,消去V或p可得出准静态绝热过程中V与T或p与T间的关系,分别为
Vγ−1T=C2(r˚H)
(4.3.8)
和
pγ−1T−γ=C3(R˚⊕1)
(4.3.9)
式(4.3.7)、式(4.3.8)和式(4.3.9)都称为理想气体的准静态绝热过程方程,它们是理想气体在同一个准静态绝热过程中两个参量所满足的关系。式中 C1 、 C2 和 C3 是三个不同的常量。
理想气体的准静态绝热过程在 p-V 图中是一条曲线,称为绝热线,如图 4-8 中曲线 AC 所示。图中还给出了该气体经过状态 A(pA,VA,TA) 的准静态等温过程的曲线 AB (等温线)。从图中可以看出,绝热线比等温线陡些。这可以从两个方面进行说明。
(1) 从数学角度来看 对等温过程有 pV=常量,求全微分可得等温线在 A 点的斜率为
(dVdp)#a=−VAPA(4.3.10)
对绝热过程方程 pV' = 常量,求全微分可得绝热线在 A 点的斜率为
(dVdp)#B=−γVAPA(4.3.11)
由于 γ>1 ,在 A 点处,绝热线的斜率要比等温线的斜率的绝对值大一些,所以绝热线比等温线陡些。
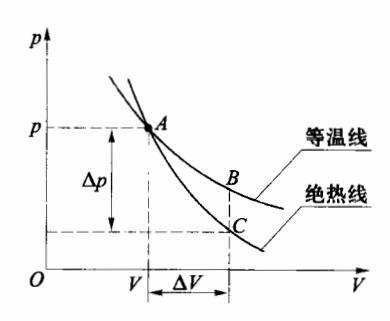
图 4-8 绝热过程与等温过程比较
(2) 从物理角度来看 根据 p = nkT,假设气体从同一状态 A 出发,分别经准静态等温过程和绝热过程做相同的体积膨胀 ΔV (图 4-8)。在这两过程中,气体压强都将减小。在等温膨胀中,压强的减小只是由于体积变大引起分子数密度 n 的减小,p 只受 n 减小的影响;而在绝热膨胀过程中,不仅 n 减小,而且由于在绝热条件下对外做正功,内能减少,所以温度 T 下降,p 受到 n 与 T 共同减小的影响。所以,气体由某状态发生相同程度的体积膨胀时,绝热过程中压强下降幅度比等温过程中大,因此绝热线比等温线陡些。
利用绝热过程方程可以计算准静态绝热过程中气体对外所做的功。
假设一定量的理想气体由初态 A(p1,V1,T1) 经准静态绝热过程变化到末态 B(p2,V2,T3) ,该过程中气体对外做功为
W=∫V1V2pdV
过程中任意状态的 p、V 与初态 p1 、 V1 间关系为 pV′=p1V1′ ,由此得 p=V′p1V1′ ,将此式代入功的表述式,有
W=p1V1γ∫V1V2VγdV=p1V1γ1−γ1(V2γ−11−V1γ−11)=γ−11(V1γ−1p1V1γ−V2γ−1p2V2γ)
经整理,得
W=γ−1p1V1−p2V2(4.3.12)
4.3.2 多方过程
气体在实际的状态变化过程中,往往既不能保证其温度不变,又不能保证完全不与外界交换热量。实际上进行的过程,其过程方程常具有下列形式:
pVn=常量(4.3.13)
满足这一关系的过程称为多方过程。该式叫作多方过程的过程方程,式中n为一常量,称为多方指数,不同的多方过程,n的取值不同。显然,当n=1时,此式表示等温过程;当 n=γ 时,此式表示绝热过程;而当n=0时,此式表示等压过程; n→∞ 时,式(4.3.13)表示的是等体过程。
理想气体在多方过程中功的计算与绝热过程时类似,只是将绝热过程时的 γ 换成n即可。例如当理想气体从初态 A(p1,V1,
讨论:在两条给定的等温线间, 定量的理想气体所进行的两个绝 热膨胀过程的功的关系
被隔板挡在容器一侧的理想气体、 当去掉隔板后自由膨胀至整个容 器过程中做的功,内能和温度变化 是什么?这一过程叫作理想气体 的自由膨胀 T1 )经准静态多方过程达到末态 B(p2,V2,T2) 时,气体对外做功为
Wn=∫v1v2pdV=p1V1n∫v1v2VndV=n−1p1V1−p2V2
(4. 3. 14)
上式中利用了多方过程方程 p1V1n=pV1n 。
下面计算理想气体在多方过程中的摩尔热容 Cn,m 。根据热力学第一定律 Q=ΔE+W ,对于多方过程有
MmCn,m(T2−T1)=MmCV,m(T2−T1)+n−1p1V1−p2V2
用 Mm(T2−T1) 除上式,并考虑到理想气体物态方程 pV=MmRT ,可得
Cn,m=CV,m−n−1R
(4.3.15)
根据迈耶公式 Cp,m = R 及气体热容比的定义 γ=Cv,mCp,m , 最终得出理想气体多方过程的摩尔热容 Cs,m
Cn,m=n−1n−γCν,m(4.3.16)
由上式可以看出, Cn,m 可正可负。当 n<1 或 n>γ 时, Cn,m 为正值,表示过程中气体吸热时温度升高;当 1<n<γ 时, Cn,m 为负值,表示该过程中气体吸热时温度反而下降。
例题 4-2
10 mol 刚性多原子分子理想气体,最初压强为 1 atm,温度为300 K,现经一准静态绝热过程,压强增至 16 atm。试求:
- (1) 气体内能的增量;
- (2) 该过程中气体所做的功;
- (3) 若气体由初态经一等温过程,体积变化到相同的终态体积(即变化到绝热过程中压强增至 16 atm 时的体积),则此时气体的压强是多少?
解:(1) 刚性多原子分子理想气体的分子自由度为 i=6,其摩尔定容热容 Cv,m 、摩尔定压热容 Cp,m 和热容比 γ 分别为 Cv,m=3R 、 Cp,m=4R 和 γ=Cp,m/Cv,m=4/3 。
在准静态绝热过程中,有
p1γ−1T1−γ=p2γ−1T2−γ.
所以
T2=(p2p1)γ1−γT1=(161)4/31−4/3T1=2T1
气体内能的增量为
ΔE=MmCV,m(T2−T1)=MmCV,m(2T1−T1)
=10×3×8.314×300 J=7.48×104 J
(2) 绝热过程中,
Q=ΔE+W=0
所以
W=−ΔE=−7.48×104 J
另解(直接求准静态绝热过程中的功): 在准静态绝热过程中,有
p1V1γ=p2V2γ
所以
V2=(p2p1)γ1V1=(161)4/31V1=81V1
气体做功为
W=∫V1V2pdV=γ−1p1V1−p2V2=γ−1p1V1−2p1V1
=−γ−1p1V1=−γ−11MmRT1
代入数值,得
W=−4/3−11×10×8.314×300 J=−7.48×104 J
(3) 因为是等温过程,所以有 p2V2=p1V1
所以
p2=V2p1V1=8p1=8
atm
(小于绝热膨胀到相同体积时的压强 16 atm!)
例题 4-3
某种刚性双原子分子理想气体经历如图所示的准静态过程,求气体在该过程的摩尔热容。
T2=4T1
过程中系统内能增量为
ΔE=MmCV,m(T2−T1)=3MmCV,mT1=215MmRT1
过程中系统对外所做的功为
W=2(p1+p2)(V2−V1)=23p1V1=23MmRT1
过程中系统吸热为
Q=ΔE+W=215MmRT1+23MmRT1=9MmRT1

图 4-9 例题 4-3图
而系统吸热又可写为
Q=MmCm(T2−T1)
所以可得气体在该过程的摩尔热容为 Cm=3R=24.94 J⋅mol−1⋅K−1
