跳到主要内容

3.9 近平衡态的输运过程

以上各节讨论的是气体在平衡态下的性质,实际上,许多问题都涉及气体由非平衡态向平衡态的变化过程。例如由于气体

内各处温度不均匀发生的热传导现象、由于密度不均匀发生的扩散现象、由于各层流速不同发生的黏性现象,都是典型的由非平衡态趋向平衡态的变化过程,这三种过程统称为输运过程。在气体由非平衡态向平衡态的变化过程中,分子的热运动和分子间的频繁碰撞起着关键作用。

3.9.1 黏性现象​

当气体在整体向前流动时,如果各层流速不同,那么相邻的气体流层将会通过它们之间的接触面互施作用力,流速较大的气体流层所受作用力与流速反向,阻碍其运动;而流速较小的流层所受作用力的方向与流速同向,使其加速。这种现象称为内摩擦现象或黏性现象。流层之间所互施的作用力称为内摩擦力或黏性力。

如图 3-10 所示为气体沿 y 轴方向作分层定向流动,各层流速 u 随坐标 z 的增加而增加。在 z=z0z=z_0 处取一垂直于 z 轴的截面,其面积为 ΔS\Delta S 。实验证明,该截面上下两层气体(图 3-10 中 A 流层和 B 流层)间互施的作用力 F 与气体在该处流速的梯度 (dudz)z0\left(\frac{\mathrm{d}u}{\mathrm{d}z}\right)_{z_0} 及面积 ΔS\Delta S 成正比,以 η\eta 为比例系数,可得如下方程

F=±η(dudz)ΔS(3.9.1)F = \pm \eta \left(\frac{\mathrm{d}u}{\mathrm{d}z}\right) \Delta S \tag{3.9.1}

该式称为牛顿黏性定律,其中比例系数 η\eta 称为黏度。在国际单位制中, η\eta 的单位是 Pa·s(帕斯卡秒)。若 F 为正值,则力 F 与流速 u 同向,是作用于流速较小的气体流层(这里为 B 流层)的力;若 F 为负值,则 F 与 u 反向,是作用于流速较大的气体流层(这里为 A 流层)的力。

从气体动理论观点来看,当气体流动时,分子除了具有热运动速度外,同时还具有定向运动速度。由于热运动,处于 ΔS\Delta S 截面以上的 A 流层中的分子将携带着较大的定向速度通过 ΔS\Delta S 运动到下面流速较小的 B 流层中,与 B 流层中的分子碰撞,使 B 流层中的分子定向运动速度增加;同样,B 流层中的分子也会携带着较小的定向速度运动到达流速较大的 A 流层中,与 A 流层中的分子碰撞,使 A 流层中的分子定向运动速度减小。结果,相当于在 A 流层产生了减速的作用力,同时在 B 流层产生了加速的作用力。

黏度η可根据分子动理论得出,其表达式为

η=13ρ vλ‾(3.9.2)\eta = \frac{1}{3}\rho \, \overline{v\lambda} \tag{3.9.2}

式中, ρ\rho 为气体的质量密度, vˉ\bar{v} 为分子热运动的平均速率, λˉ\bar{\lambda} 为平均自由程。

3.9.2 热传导现象​

当气体内各部分温度不相等时,将有热量从温度较高的部分向温度较低的部分传递,这种现象称为热传导现象。假设气体沿z 轴方向温度逐渐升高(图 3-11),在 z=z0z=z_0 处取垂直于 z 轴的面积为 ΔS\Delta S 的截面。实验证明,单位时间内通过面积 ΔS\Delta S 从温度较高的 A 部分向温度较低的 B 部分传递的热量 dQdt\frac{\mathrm{d}Q}{\mathrm{d}t} 与该处温度的梯

度 (dTdz)t0\left(\frac{\mathrm{d}T}{\mathrm{d}z}\right)_{t_0} 和面积 ΔS 成正比,以 κ 为比例系数,便可得到如下方程

dQdt=−κ(dTdz)t0ΔS(3.9.3)\frac{\mathrm{d}Q}{\mathrm{d}t} = -\kappa \left(\frac{\mathrm{d}T}{\mathrm{d}z}\right)_{t_0} \Delta S \tag{3.9.3}

此式称为傅里叶定律,负号表示热量向温度降低的方向传递。比例系数 κ\kappa 称为热导率或称导热系数,单位为 W⋅m−1⋅K−1\mathbf{W} \cdot \mathbf{m}^{-1} \cdot \mathbf{K}^{-1} 。

从分子动理论观点来看,温度是分子平均动能的量度,气体中温度较高的 A 部分的分子,其平均动能比温度较低的 B 部分的分子的平均动能大。由于热运动,处于 A、B 两部分的分子将有一些发生交换,从而使温度较低的 B 部分的分子平均动能增加,使温度较高的 A 部分的分子平均动能减小。从宏观上看,这导致了热量从高温处向低温处迁移。

由分子动理论可以证明

κ=13n v‾λi2k(3.9.4)\kappa = \frac{1}{3} n \, \overline{v} \lambda \frac{i}{2} k \tag{3.9.4}

式中,n 为气体分子数密度,k 为玻耳兹曼常量。对于刚性分子,i=t+r,对于非刚性分子,i=t+r+2s,其中t,r,s 分别为气体分子的平动、转动和振动自由度。

3.9.3 扩散现象​

在混合气体内部,如果某种气体的密度不均匀,这种气体分 子将从密度较大的地方向密度较小的地方迁移,这种现象叫作扩

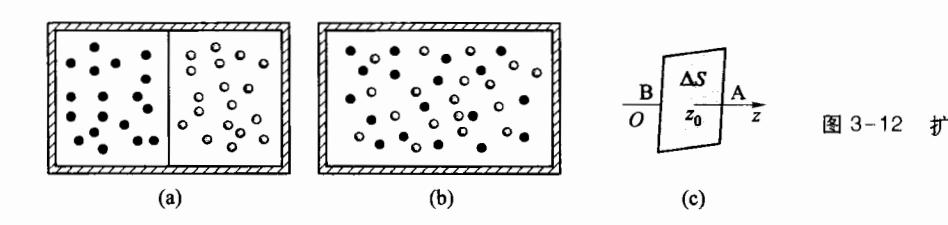
散现象。假设容器中有分子质量相同或相近的两种气体(如 N2N_2 和 CO 两种气体),最初它们被隔板分隔开来(图 3-12),假设它们的温度和压强都相同,当隔板打开时,两种气体便互相扩散。由于分子质量相近、温度相同、压强相等,所以,在扩散过程中将不存在由于两种分子的平均动能差或压强差引起的宏观气流,而只存在由于密度不同导致的单纯的扩散现象。现只考虑一种气体的扩散。假设该气体的密度沿 z 轴方向随 z 的增加而增加。实验证明,气体分子在单位时间内通过 ΔS\Delta S 面的质量 dmdt\frac{dm}{dt} 与该处

气体质量密度的梯度 (dρdz)z0\left(\frac{d\rho}{dz}\right)_{z_0} 和面积 ΔS\Delta S 成正比,以 D 为比例系数.则可得如下方程:

dmdt=−D(dρdz)ΔS(3.9.5)\frac{\mathrm{d}m}{\mathrm{d}t} = -D\left(\frac{\mathrm{d}\rho}{\mathrm{d}z}\right) \Delta S \tag{3.9.5}

此式称为菲克定律,负号表示质量迁移朝密度小的方向进行。比例系数 D 称为气体的扩散系数,单位是 m2⋅s−1m^2 \cdot s^{-1} 。

从气体动理论观点来看,由于分子热运动, ΔS\Delta S 面两侧的分子都会通过 ΔS\Delta S 到达另一侧,但是,由于存在密度差,因此在相同时间内,由 A 侧(密度较高)通过 ΔS\Delta S 向 B 侧(密度较低)迁移的分子必然多于反向迁移的分子,从而形成质量迁移。

由分子动理论可以推导得出

D=13vˉ λ‾(3.9.6)D = \frac{1}{3}\bar{v}\,\overline{\lambda} \tag{3.9.6}