3.10 实际气体的范德瓦尔斯方程
我们知道,理想气体只是从实际气体抽象出来的理想模型, 实际气体只有在压强不太高、温度不太低的情况下,才可近似看 成是理想气体。但对于实际气体,如果处于压强较高、温度较低
情况下,这时分子间距较小,分子的体积和分子间的相互作用已不可忽略,这种气体不再遵从理想气体的物态方程。因此必须寻找适用于真实气体的新的物态方程。有关真实气体的性质,不论在实验上还是在理论上,人们都做了大量的工作,也已提出了多种形式的物态方程,其中形式比较简单,而物理意义又比较清晰的就是著名的范德瓦耳斯方程。
范德瓦耳斯方程是考虑到真实气体的分子体积和分子力后, 对理想气体物态方程加以修正得到的。
考虑 1 mol 理想气体,其物态方程是
式中, 是分子自由活动的空间,因为不考虑分子的体积,因此 也是容器的容积。现在容积为 的容器中盛装的是一定量的真实气体,因为每一个分子都具有一定的体积,所以气体分子在容器中自由活动的空间范围将减小。 假设用 b 表示容器中所有分子占有的空间,因此,分子实际自由活动空间将减小为( -b),则物态方程修正为
b 是与具体分子有关的量,对于给定的气体,b 有确定的数值。
下面考虑分子作用力的影响。
我们知道,当分子间距离 的数量级为 m)时,分子力 F=0。当 时,分子间表现为斥力。而当 时,分子向表现为斥力。而当 时,分子力表现为引力,且随距离的增大迅速减小,当距离大于某一量值 r(r) 称为分子力有效作用距离,量值可达 m)时,分子间作用力可忽略不计。容器中的气体作用在器壁上的压强是大量气体分子对器壁撞击的集体体现。理想气体分子在与器壁碰撞时,不受其他气体分子的影响,而对于真实气体的分子来说,在与器壁碰撞的同时,它还受到其他分子对它的作用力。显然,真实气体对器壁的压强将不同于理想气体情形。
以分子为中心、以有效作用距离 r 为半径的球,称为引力作用球。图 3-13 给出了在容器中不同位置的两个作用球。对于容器内部的分子 1 来说,其作用球内的分子相对于它是对称分布的,因此它所受引力互相抵消。但对于靠近容器器壁的分子 2 来说,情形有所不同。分子 2 的引力作用球有一部分在容器外,因此,作用球内的其他分子相对于分子 2 来说不是对称分布,分子 2 将受到一个指向气体内部的分子引力的合力,设合力的大小为 。该力使分子 2 飞向器壁的动量减小,从而减小对器壁的冲力,所以分子引力的作用将减小对器壁的压强,我们称这个减小的压强为内压强,用 表示。根据压强的定义可知:
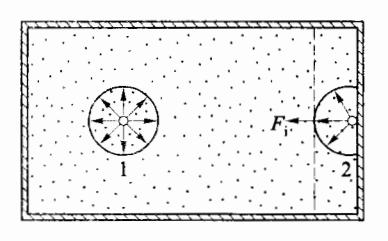
图 3-13 分子力作用球面
= (单位时间内与单位面积的器壁相碰的分子数)× 由于单位时间内与单位面积的器壁相碰撞的分子数与分子数密度n成正比, 与F,成正比,而F,又与n成正比,因此
(3. 10. 2)
式中, a 为比例系数, 其值由气体的性质决定。将这一关系代人式(3.10.1), 经过整理得
(3. 10. 3)
这就是 1 mol 实际气体的范德瓦耳斯方程。式中 是 1 mol 真实气体的范德瓦耳斯常量,其数值需用实验测定。表 3-1 列出了几种实际气体的 a 和 b 的值。可以看出,对于不同的气体,a 和 b 的值也不同。
| 气体 | a/(Pa·m6·mol-2) | b/(10-3 m3 · mol-1) |
|---|---|---|
| 氦 | 0.003 4 | 0.024 |
| 氢 | 0.024 8 | 0.027 |
| 氙 | 0.135 8 | 0.032 |
| 氨 | 0.140 8 | 0.039 |
| 氧 | 0.137 8 | 0.032 |
| 水蒸气 | 0.553 2 | 0.030 |
| 二氧化碳 | 0.363 8 | 0.043 |
表 3-1 范德瓦耳斯常量 a 和 b 的实验值
思考题与习题
-
3.1 推导理想气体压强公式时,何处用到理想 3.4 两瓶不同种类气体的假设?何处用到平衡态的条件?何处用到统 都相同,但体积不同,问: 计平均的概念? (1)单位体积内的分
-
3.2 当气体的温度为 时,能否说气体中每个分子的温度也是 ? 气体中有的分子运动速度快,有的速度慢,能否说速度快的分子温度高,速度慢的分子温度低?
-
3.3 气体处于平衡态时,分子的平均速度为多大?平均速率为多大?
-
3.4 两瓶不同种类的理想气体,如压强和温度 都相同,但体积不同,问:
- (1) 单位体积内的分子数是否相同?
- (2) 单位体积内的气体质量是否相同?
- (3) 单位体积内气体分子的总平动动能是否相同?
-
3.5 容器中装有一定量的某种理想气体,当气体处于某一状态时,如果气体内:
-
(1)各部分的压强相等,此状态是否一定是平 衡态?
-
(2)各部分的温度相等,此状态是否一定是平衡态?
-
(3) 各部分的压强相等,密度相同,此状态是否一 定是平衡态?
-
3.6 一定量理想气体,当温度保持恒定时,其压 强随体积的减小而增大;当体积保持恒定时,其压强 | 和平均碰撞频率与温度的关系如何? 随温度的升高而增大。这两种使气体压强增大的过 程,从分子动理论的微观观点分析有何区别?
-
3.7 某种刚性双原子分子理想气体处于温度为 T 的平衡状态,分别写出下列各量的表达式:
- (1) 分子的平均平动动能;
- (2) 分子的平均总动能;
- (3) 分子的平均总能量;
- (4) 1 mol 气体分子的总转动动能;
- (5) 1 mol 气体的内能。
若为非刚性分子呢?
-
3.8 分子的每一个振动自由度的平均能量是 多少?
-
3.9 气体分子速率分布函数 f(v) 的物理意义是 什么?下列各表示什么(其中 N 为气体分子总数)?
-
-
(3) ; (4) ;
-
-
-
3.10 试在同一图中画出同种理想气体处于不 同温度的速率分布曲线和处于相同温度的不同理想 气体的速率分布曲线。
-
3.11 有人认为气体分子的最概然速率就是速 率分布中的最大速率值,对不对?
-
3.12 装有理想气体的容器上有一小孔,气体不 断从小孔泻出(假设小孔很小,分子的泻出不影响容 器内的平衡态),那么泻出的分子速率是否满足麦克 斯韦速率分布? 其平均速率是否与容器内分子的平 | 均速率相同?
-
3.13 一定量的理想气体,保持体积不变,当温度 增加时,分子的平均碰撞频率和平均自由程各如何变化?
-
3.14 理想气体等压膨胀时,分子的平均自由程
-
3.15 理想气体等温压缩时,分子的平均自由程 和平均碰撞频率与压强的关系如何?
-
3.16 在一定温度和体积下,由理想气体物态方 程和范德瓦耳斯方程算出的压强哪个大?
-
3.17 如果每秒有1023个氧气分子沿着与容器器 壁的法线成 45°角的方向,以 500 m·s-1的速率撞击在 器壁 2.0 cm²的面积上, 若碰撞是弹性的, 求氧气的 压强。
-
3.18 一容器贮有氧气,其压强 p=1.0 atm, 温度 为 t= 27 ℃。求:
- (1) 单位体积内的分子数;
- (2) 氧气分子的质量:
- (3) 氧气的质量密度 ;
- (4) 氧气分子的平均平动动能。
-
3.19 某气体的压强为 atm. 密度为 ρ=1.24×10-2 kg·m-3,导出该气体分子的方均根速率 与压强、密度之间的关系并计算其数值。
-
3.20 若某种刚性双原子分子理想气体处于温 度为 300 K 的平衡态, 求下列各量:
- (1) 分子的平均平动动能;
- (2) 分子的平均总动能;
- (3) 分子的平均总能量;
- (4) 1 mol 气体分子的总转动动能;
- (5) 1 mol 气体的内能。
-
3.21 在某一温度下,将体积和压强都相同的氦 气和氢气(均视为刚性分子理想气体)混合,求所有氢 气分子所具有的能量在混合气体系统总能量中所占 的百分比。
-
3.22 计算在 300 K 温度下,氢气分子的方均根速率、平均速率、最概然速率及其平均平动动能。
-
- 23 分别计算氧气处于温度为 300 时,速率在 3 000~3 010 m·s-1和 m·s-1间的分子数的百分比,并计算 300 和 500 两种温度下速率在 m·s-1之间的分子百分数的比。(可将 dv 近似地以 m·s-1取代。)
-
- 24 拉萨海拔约 3 600 m,设大气温度 t = 27 °C,而且处处相同,求拉萨的气压。(空气的摩尔质量 kg·mol-1,海平面处的气压 atm。)
- 3.25 氮气分子的平均有效直径为 3.8×10-10 m。
-
(1) 求在标准状态下, 氦气分子的平均碰撞频率 和平均自由程;
-
(2) 若压强降到无线电所用的电子管内真空度所要求的压强 1.33×10-3 Pa 时,温度仍为 0 ℃,求此时分子的平均自由程和平均碰撞频率。
-
3.26 气缸内盛有一定量的氢气(可视为理想气体),当温度不变而压强增大一倍时,氢气分子的平均碰撞频率和平均自由程的变化情况怎样?
-
3.27 今测得氮气在 0 ℃ 时的黏度为 16.6× N·s·m-2,试计算氮气分子的平均有效直径和碰撞截面面积。
-
3.28 热水瓶胆两层玻璃间距为 3.00 mm,求在 17 °C下使玻璃间隔内的空气压强降到多少时,才能使空气的导热系数等于大气压下导热系数的 1%,从而使热水瓶起保温作用(已知空气分子的有效直径为 3.0×10-10 m)。
-
3.29 氧气在标准状态下的扩散系数为 1.0× 10-5 m2·s-1,求氧气分子的平均自由程。
- 3.30 求气体分子的平均速率:
- (1) 在 0~vp 之间;
- (2) 大于 v,。
- (可利用积分公式: ,
3.31 试从玻耳兹曼能量分布函数,求证自由粒子的能量 的平均值为 。(可利用积分公式