从本节开始讨论刚体定轴转动动力学的内容。
2.2.1 相对固定轴的力矩
力矩的定义在第 1 章质点角动量定理中已有叙述。该定理所涉及的质点角动量与力矩都是相对同一点的。本节将要讨论的内容是定轴转动动力学,所涉及的力矩是相对于转轴的。一般来说,当力 F 以任意方向作用于刚体时,对于刚体的定轴转动有影响的仅是力 F 中与转轴垂直的分力。如图 2-5 所示,刚体(图中没有画出)绕 Oz 轴旋转,M 是刚体内某一垂直转轴的转动平面,M 平面与 Oz 轴相交于 O 点。力 F 的作用点 P 位于 M 平面内,P 点相对 O 点的位矢为 F 。假设力 F 的作用线不在 M 平面内而是与 M 平面有一夹角。力 F 投影到 M 平面内的分力与转轴垂直,记为 F ⊥ F_{\perp} F ⊥ F / / F_{//} F // M / / M_{//} M // r × F / / r \times F_{//} r × F // M ⊥ M_{\perp} M ⊥ r × F ⊥ r \times F_{\perp} r × F ⊥
刚体的转动定律
需考虑作用力中垂直转轴的分力的力矩即可。当然,这个分力对定轴转动起作用的前提是,其作用线不能通过转轴,即图中 r 与 F ⊥ F_{\perp} F ⊥ θ \theta θ M ⊥ M_{\perp} M ⊥ M ⊥ M_{\perp} M ⊥ ∣ M ⊥ ∣ = ∣ r ∣ ∣ F ⊥ ∣ sin θ = ∣ F ⊥ ∣ d |M_{\perp}| = |r| |F_{\perp}| \sin \theta = |F_{\perp}| d ∣ M ⊥ ∣ = ∣ r ∣∣ F ⊥ ∣ sin θ = ∣ F ⊥ ∣ d F ⊥ F_{\perp} F ⊥ F ⊥ F_{\perp} F ⊥
2.2.2 刚体定轴转动定律
式中 a i a_i a i Δ m i \Delta m_i Δ m i
切向:
F i sin θ i + F μ i sin φ i = Δ m i a i i = Δ m i r i β F_i \sin \theta_i + F_{\mu_i} \sin \varphi_i = \Delta m_i a_{ii} = \Delta m_i r_i \beta F i sin θ i + F μ i sin φ i = Δ m i a ii = Δ m i r i β 法向:
− ( F i cos θ i + F t h cos φ i ) = Δ m i a i n = Δ m i r i ω 2 -(F_i \cos \theta_i + F_{th} \cos \varphi_i) = \Delta m_i a_{in} = \Delta m_i r_i \omega^2 − ( F i cos θ i + F t h cos φ i ) = Δ m i a in = Δ m i r i ω 2 式中, β \beta β ω \omega ω τ \tau τ
r i F i sin θ i + r i F p i sin φ i = Δ m i r i 2 β r_i F_i \sin \theta_i + r_i F_{p_i} \sin \varphi_i = \Delta m_i r_i^2 \beta r i F i sin θ i + r i F p i sin φ i = Δ m i r i 2 β 将上式对刚体中所有质元求和,有
律,有
∑ i r i F i sin θ i + ∑ i r i F ϕ i sin φ i = ( ∑ i Δ m i r i 2 ) β ( 2.2.1 ) \sum_{i} r_{i} F_{i} \sin \theta_{i} + \sum_{i} r_{i} F_{\phi_{i}} \sin \varphi_{i} = \left(\sum_{i} \Delta m_{i} r_{i}^{2}\right) \beta \qquad (2.2.1) i ∑ r i F i sin θ i + i ∑ r i F ϕ i sin φ i = ( i ∑ Δ m i r i 2 ) β ( 2.2.1 ) 式(2.2.1)左边第一项是所有外力相对转轴的力矩之和,称为合外力矩,记为
M = ∑ i r i F i sin θ i ( 2.2.2 ) M = \sum_{i} r_i F_i \sin \theta_i \qquad (2.2.2) M = i ∑ r i F i sin θ i ( 2.2.2 ) 式(2.2.1)左边第二项是刚体内部所有质元之间相互作用力的力矩之和,称为合内力矩。与质点系角动量定理中遇到的情形
图 2-6 定轴转动定律
一样,由于内力成对出现,每一对内力大小相等、方向相反且作用在同一条直线上,力的作用线到转轴的距离相同,所以每对内力对转轴的力矩之和等于零,进而整个刚体所受的合内力矩为零,即
∑ i r i F p i sin φ i = 0 \sum_{i} r_i F_{p_i} \sin \varphi_i = 0 i ∑ r i F p i sin φ i = 0 式(2.2.1)右边括弧中出现的是一个新的物理量, 称为转动惯量,以 / 表示, 定义为
I = ∑ i Δ m i r i 2 ( 2.2.3 ) I = \sum_{i} \Delta m_i r_i^2 \qquad (2.2.3) I = i ∑ Δ m i r i 2 ( 2.2.3 ) 转动惯量的物理意义将在下文说明。这样,式(2.2.1)可以简记为
M = I β (2.2.4) M = I\beta \tag{2.2.4} M = I β ( 2.2.4 ) 此式表明:在定轴转动中,刚体的角加速度与刚体所受的合外力矩成正比,与刚体的转动惯量成反比。这一结论称为刚体定轴转动定律。应该特别注意的是,这里的合外力矩、转动惯量以及角加速度都是相对同一转轴的。对于定轴转动来说,力矩矢量、角加速度矢量以及角速度矢量的方向都是沿着转轴的,只有两个转向,所以可按标量处理,式(2.2.4)就是一个标量式。计算时可依据给定转轴,人为选定一个转向作为正方向,凡与选定正方向转向一致的M、 β \beta β ω \omega ω θ \theta θ
将牛顿第二定律表达式 F=ma 与式(2.2.4)进行比较,从牛顿第二定律到定轴转动定律,力演变为力矩,加速度演变为角加速度,质量(物体平动惯性大小的量度)演变为转动惯量(物体转动惯性大小的量度)。可见,两者关系一一对应。从处理质点(或刚体)平动问题的牛顿第二定律到处理刚体定轴转动问题的转动定律,二者的地位是相当的。
2.2.3 转动惯量
1. 转动惯量的物理意义
转动惯量的定义式(2.2.3)表明,刚体绕定轴的转动惯量等于刚体中各个质元的质量与该质元到转轴距离平方的乘积之和。在牛顿第一定律的讨论中曾经提到,当物体不受外力或所受合外力为零时,物体将保持原有的(静止或匀速直线)运动状态不变,物体的这种特性称为惯性,惯性大小的量度是物体的质量。物体的转动问题与之类似,一个砂轮在接通电源后做
物体受的合力为零,运过状态重小变购。
高速转动,关闭电源后,砂轮还要转动一段时间后才能停下来。砂轮轴上以及周围空气的摩擦阻力矩直接影响砂轮停电后持续转动的时间。所受阻力矩越小,砂轮持续转动的时间越长。设想如果阻力矩趋于零,砂轮将一直持续转动下去。显然,砂轮具有保持原有转动状态不变的特性,这种特性称为转动惯性。正像质量是物体平动惯性大小的量度一样,转动惯量是物体转动惯性大小的量度。转动惯量是物体本身的属性,与物体的运动状态无关。
从转动惯量的定义可知,刚体相对定轴的转动惯量本质上是刚体内各个质元相对该定轴的转动惯量之和。因此,转动惯量具有可加性,这种可加性可以推广到多个刚体之间的转动惯量求和,即如果刚体 1 对给定转轴的转动惯量为 I 1 I_1 I 1 I 2 I_2 I 2 I = I 1 + I 2 I=I_1+I_2 I = I 1 + I 2
从转动惯量的定义还知道: 刚体转动惯量的大小, 首先与刚体本身的质量有关, 质量越大, 转动惯量就越大; 其次与刚体的质量分布有关, 同样质量的刚体, 质量分布离轴越远的, 其转动惯量就越大; 第三与转轴的位置有关, 同一刚体, 相对不同转轴具有不同的转动惯量。这三点通常称为转动惯量的三要素。
在国际单位制中,转动惯量的单位为 kg·m²(千克二次方米)。 2. 转动惯量的计算
式(2.2.3)是转动惯量的基本定义,该式对于质量是离散分布的情况计算时较为方便。例如,对于一个由两个质点组成的质点系,质量为 m 1 m_1 m 1 r 1 r_1 r 1 m 2 m_2 m 2 r 2 r_2 r 2 I = I 1 + I 2 = m 1 r 1 2 + m 2 r 2 2 I=I_1+I_2=m_1r_1^2+m_2r_2^2 I = I 1 + I 2 = m 1 r 1 2 + m 2 r 2 2 r 2 d m r^2dm r 2 d m
I = ∫ r 2 d m (2.2.5) I = \int r^2 \, \mathrm{d}m \tag{2.2.5} I = ∫ r 2 d m ( 2.2.5 ) 积分遍及整个刚体。此式对于质量均匀分布且形状规则的刚体 计算起来较为方便。对于质量分布不均匀、形状不规则的刚体, 其转轴惯量一般需要通过实验测定。
求:(1)质量为m、半径为R的均质细圆环绕通过圆心且垂直环面的转轴的转动惯量:(2)质量为m、半径为R的均质圆盘绕通过圆心且垂直盘面的转轴的转动惯量。
解:(1) 如图 2-7(a)所示,圆环的质量线密度为 λ = m / 2 π R \lambda = m/2\pi R λ = m /2 π R d m = λ d l dm = \lambda dl d m = λ d l d I = R 2 d m = R 2 λ d l dI = R^2 dm = R^2 \lambda dl d I = R 2 d m = R 2 λ d l
I = ∫ d I = ∫ R 2 d m = ∫ 0 2 π R R 2 λ d l = m R 2 I = \int dI = \int R^2 dm = \int_0^{2\pi R} R^2 \lambda dl = mR^2 I = ∫ d I = ∫ R 2 d m = ∫ 0 2 π R R 2 λ d l = m R 2
图 2-7 圆环与圆盘的转动惯量
此结果与薄壁圆筒相对中心对称轴的转动惯量相同。
(2) 如图 2-7(b) 所示,圆盘的质量面密度 σ = m / π R 2 \sigma = m/\pi R^2 σ = m / π R 2 d I = r 2 d m = r 2 σ d S = r 2 σ ⋅ 2 π r d r dI = r^2 dm = r^2 \sigma dS = r^2 \sigma \cdot 2\pi r dr d I = r 2 d m = r 2 σ d S = r 2 σ ⋅ 2 π r d r
I = ∫ d I = ∫ 0 R 2 π σ r 3 d r = 1 2 m R 2 I = \int dI = \int_0^R 2\pi \sigma r^3 dr = \frac{1}{2} mR^2 I = ∫ d I = ∫ 0 R 2 πσ r 3 d r = 2 1 m R 2 此结果与圆柱相对中心对称轴的转动惯量相同。另外,圆盘形滑轮也常常采用此式作为转动惯量。
例题 2-5
如图 2-8 所示,求质量为 m、长为 l 的均匀细棒相对如下各轴的转动惯量:(1)过棒的中心 O 点并与棒垂直的轴;(2)过棒的端点 O'点并与棒垂直的轴;(3)过与中心 O 点相距为 d 的 O'' 点并与棒垂直的轴。
图 2-8 细棒的转动惯量
解:(1) 以 O 为原点,沿棒长方向建立 z 轴,在距原点 x 处取线元 dx,相应质量 d m = λ d x dm = \lambda dx d m = λ d x λ = m / l \lambda = m/l λ = m / l d I = x 2 d m = x 2 λ d x dI = x^2 dm = x^2 \lambda dx d I = x 2 d m = x 2 λ d x
I o = ∫ d I = ∫ − l / 2 l / 2 x 2 λ d x = 1 12 m l 2 I_o = \int dI = \int_{-l/2}^{l/2} x^2 \lambda \, dx = \frac{1}{12} m l^2 I o = ∫ d I = ∫ − l /2 l /2 x 2 λ d x = 12 1 m l 2 (2) 将坐标原点移至 0'点,整个棒相 对过 0'点轴的转动惯量为
I o ′ = ∫ d I = ∫ 0 l x 2 λ d x = 1 3 m l 2 I_{o'} = \int dI = \int_0^l x^2 \lambda dx = \frac{1}{3} m l^2 I o ′ = ∫ d I = ∫ 0 l x 2 λ d x = 3 1 m l 2 (3) 将坐标原点移至 O''点,整个棒相 对过 O''点轴的转动惯量为
I o ∗ = ∫ d I = ∫ d − l / 2 d + l / 2 x 2 λ d x = 1 12 m l 2 + m d 2 I_{o^*} = \int dI = \int_{d-l/2}^{d+l/2} x^2 \lambda dx = \frac{1}{12} m l^2 + m d^2 I o ∗ = ∫ d I = ∫ d − l /2 d + l /2 x 2 λ d x = 12 1 m l 2 + m d 2 显然, 当 d = l / 2 d = l/2 d = l /2 I o ∗ I_{o^*} I o ∗ I o ∗ I_{o^*} I o ∗
表 2-2 列出了几种密度均匀、几何形状规则的常见刚体的转动惯量,这些结果利用转动惯量的积分式(2.2.5)可全部计算出来。
表 2-2 常见刚体的转动惯量
在工程实际中,常采用回转半径的概念。设刚体的质量为m,相对给定轴的转动惯量为I,则定义刚体相对该轴的回转半径r。为
r G = I m r_{\rm G} = \sqrt{\frac{I}{m}} r G = m I (2.2.6)
回转半径的意义为,从刚体相对该轴的转动效应来讲,刚体的质量可以视为全部集中在离轴距离为 r G r_{\rm G} r G I = m R 2 / 2 I=mR^2/2 I = m R 2 /2 r G = R / 2 r_{\rm G}=R/\sqrt{2} r G = R / 2
3. 有关转动惯量的两个定理
从上面例题 2-5 的结果中,我们得出质量为m、长为l 的均匀细棒相对过棒的中心 O 点并与棒垂直的轴的转动惯量为 I o = m l 2 / 12 I_o=ml^2/12 I o = m l 2 /12 I o ∗ = m l 2 / 12 + m d 2 I_{o^*}=ml^2/12+md^2 I o ∗ = m l 2 /12 + m d 2 I o ∗ = I o + m d 2 I_{o^*}=I_o+md^2 I o ∗ = I o + m d 2
心的转动惯量可记为 I c I_c I c I o r I_{or} I or
I = I c + m d 2 ( 2.2.7 ) I = I_c + md^2 (2.2.7) I = I c + m d 2 ( 2.2.7 ) 式(2.2.7)具有普遍意义,它表明:刚体相对任一转轴的转动惯量 I等于刚体相对通过质心并与之平行的轴的转动惯量 I c I_c I c
有关转动惯量的另一个定理是正交轴定理。设有一任意形状的平面均质薄板刚体,取薄板平面为 Oxy 平面建立坐标系,垂直薄板方向为 z 轴,如图 2-9 所示。薄板相对 x 轴的转动惯量为 I x = ∫ y 2 d m I_x = \int y^2 \mathrm{d}m I x = ∫ y 2 d m I y = ∫ x 2 d m I_y = \int x^2 \mathrm{d}m I y = ∫ x 2 d m I z = ∫ r 2 d m = ∫ ( x 2 + y 2 ) d m = ∫ x 2 d m + ∫ y 2 d m I_z = \int r^2 \mathrm{d}m = \int (x^2 + y^2) \mathrm{d}m = \int x^2 \mathrm{d}m + \int y^2 \mathrm{d}m I z = ∫ r 2 d m = ∫ ( x 2 + y 2 ) d m = ∫ x 2 d m + ∫ y 2 d m I z = I z + I z I_z = I_z + I_z I z = I z + I z
式(2.2.8)表明:平面均质薄板刚体相对垂直板面的某一转轴的转动惯量等于刚体相对通过该轴与板面交点且位于板面内的两个正交轴的转动惯量之和。这一关系称为正交轴定理。
图 2-9 正交轴定理
2.2.4 转动定律的应用
下面来看应用转动定律式(2.2.4)的两个例子。
例题 2-6
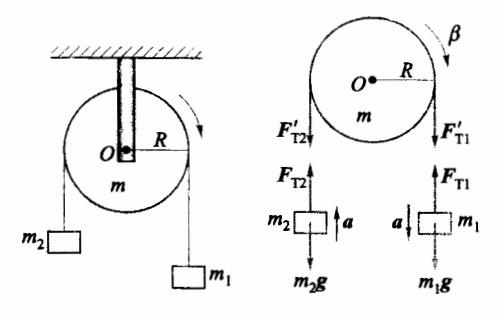
如图 2-10 所示,一轻绳跨过一质量为 m、半径为 R 的定滑轮,绳的两端各悬挂一物体,质量分别为 m 1 m_1 m 1 m 2 m_2 m 2 m 1 m_1 m 1 m 2 m_2 m 2 I = m R 2 / 2 I=mR^2/2 I = m R 2 /2
解:本题特别应该注意的是,由于定滑轮的质量不能忽略,使得定滑轮两侧的绳中张力不相等。解题步骤如下:
第一步,根据题设 m,>m,,选择定滑轮
图 2-10 滑轮质量不可忽略的物体系的运动
顺时针旋转为运动正方向,分别画出三个物体的隔离体图。
第二步,分别应用牛顿第二定律和刚体
定轴转动定律,按所选定的正方向列方程。由于绳子不可伸长,两侧物体的加速度大小相等,设其为 a。滑轮角加速度为 β \beta β m 1 m_1 m 1 m 1 g m_1g m 1 g F T 1 F_{T1} F T 1 m 1 m_1 m 1
m 1 g − F T 1 = m 1 a m_1 g - F_{T1} = m_1 a m 1 g − F T 1 = m 1 a 对物体 m 2 m_2 m 2 m 2 g m_2g m 2 g F 12 F_{12} F 12 m 2 m_2 m 2
F T 2 − m 2 g = m 2 a F_{T2}-m_2g=m_2a F T 2 − m 2 g = m 2 a 这里要特别注意,两个物体运动的正向一定要与定滑轮所选的正向一致。对定滑轮而言,右侧绳子张力大小为 F 11 ′ F'_{11} F 11 ′ F 12 ′ F'_{12} F 12 ′
F T 1 ′ R − F T 2 ′ R = I β = 1 2 m R 2 β F'_{T1}R - F'_{T2}R = I\beta = \frac{1}{2}mR^2\beta F T 1 ′ R − F T 2 ′ R = I β = 2 1 m R 2 β 由于绳子与定滑轮无相对滑动,所以物体的加速度 a 相当于定滑轮的切向加速度,根据线量与角量的关系式(2.1.11),有
a = R β a = R\beta a = Rβ 右侧绳中张力 F T 1 F_{T1} F T 1 F T 1 ′ F'_{T1} F T 1 ′ F T 2 F_{T2} F T 2 F T 2 ′ F'_{T2} F T 2 ′
F T 1 ′ = F T 1 fi F T 2 ′ = F T 2 F'_{T1} = F_{T1} \quad \text{fi} \quad F'_{T2} = F_{T2} F T 1 ′ = F T 1 fi F T 2 ′ = F T 2 这样,一共有6个方程,对应6个未知数。
第三步,求解方程组。得到 β \beta β F τ 1 F_{\tau_1} F τ 1 F τ 2 F_{\tau_2} F τ 2
β = m 1 − m 2 ( m 1 + m 2 + m / 2 ) R g , a = m 1 − m 2 ( m 1 + m 2 + m / 2 ) g \beta = \frac{m_1 - m_2}{(m_1 + m_2 + m/2)R}g, \quad a = \frac{m_1 - m_2}{(m_1 + m_2 + m/2)}g β = ( m 1 + m 2 + m /2 ) R m 1 − m 2 g , a = ( m 1 + m 2 + m /2 ) m 1 − m 2 g F T1 = 4 m 2 + m 2 ( m 1 + m 2 ) + m m 1 g F_{\text{T1}} = \frac{4m_2 + m}{2(m_1 + m_2) + m} m_1 g F T1 = 2 ( m 1 + m 2 ) + m 4 m 2 + m m 1 g , F T2 = 4 m 1 + m 2 ( m 1 + m 2 ) + m m 2 g F_{\text{T2}} = \frac{4m_1 + m}{2(m_1 + m_2) + m} m_2 g F T2 = 2 ( m 1 + m 2 ) + m 4 m 1 + m m 2 g
第四步,对结果进行简单的讨论。显然,由于 m 1 > m 2 m_1 > m_2 m 1 > m 2 F T 1 > F T 2 F_{T1} > F_{T2} F T 1 > F T 2 m → 0 m \to 0 m → 0 F T 1 = F T 2 = 2 m 1 m 2 m 1 + m 2 g F_{T1} = F_{T2} = \frac{2m_1m_2}{m_1 + m_2} g F T 1 = F T 2 = m 1 + m 2 2 m 1 m 2 g
明,只有定滑轮质量可以忽略时,绳子两侧的张力才相等。
例题 2-7
如图 2-11 所示,一质量为 m、长为 l 的均匀细棒,可绕通过其一端且与棒垂直的水平光滑固定轴 O 转动,细棒绕轴 O 的转动惯量为 I = m l 2 / 3 I=ml^2/3 I = m l 2 /3
解:转轴对细棒的作用力通过轴线,不产生力矩。因此,细棒下摆过程中只受重力矩作用。细棒所受重力的大小为 mg, 是定值, 但
图 2-11 细棒的转动
到转轴 0 的距 离随下摆角度变化,即力臂是变量,因而重
重力的作用线
力矩也是变量,所以本题采用转动定律求解时,需要进行积分计算。以细棒顺时针转动为正方向,取细棒下摆至任意 θ \theta θ l 2 cos θ \frac{l}{2}\cos\theta 2 l cos θ l 2 cos θ \frac{l}{2}\cos\theta 2 l cos θ β \beta β
M = m g l 2 cos θ = l β = 1 3 m l 2 β M = mg \frac{l}{2} \cos \theta = l\beta = \frac{1}{3} m l^2 \beta M = m g 2 l cos θ = lβ = 3 1 m l 2 β 解出
β = 3 2 g l cos θ \beta = \frac{3}{2} \frac{g}{l} \cos \theta β = 2 3 l g cos θ 此结果表明,在 [ 0 , π / 2 ] [0,\pi/2] [ 0 , π /2 ] β > 0 \beta>0 β > 0 β \beta β θ \theta θ β \beta β θ \theta θ β = d ω / d t \beta=d\omega/dt β = d ω / d t θ \theta θ ω \omega ω ω \omega ω
β = d ω d t = d ω d θ d θ d t = ω d ω d θ \beta = \frac{\mathrm{d}\omega}{\mathrm{d}t} = \frac{\mathrm{d}\omega}{\mathrm{d}\theta} \frac{\mathrm{d}\theta}{\mathrm{d}t} = \omega \frac{\mathrm{d}\omega}{\mathrm{d}\theta} β = d t d ω = d θ d ω d t d θ = ω d θ d ω 这就消去了时间 t。代人 β \beta β θ \theta θ
ω d ω = 3 g 2 l cos θ d θ \omega d\omega = \frac{3g}{2l} \cos \theta d\theta ω d ω = 2 l 3 g cos θ d θ 开始时, θ \theta θ ω \omega ω θ \theta θ ω \omega ω
∫ 0 ω ω d ω = ∫ 0 θ 3 g 2 l cos θ d θ \int_0^{\omega} \omega \, d\omega = \int_0^{\theta} \frac{3g}{2l} \cos \theta \, d\theta ∫ 0 ω ω d ω = ∫ 0 θ 2 l 3 g cos θ d θ 得到
ω = 3 g l sin θ \omega = \sqrt{\frac{3g}{l}\sin \theta} ω = l 3 g sin θ 此结果表明,在 [ 0 , π / 2 ] [0,\pi/2] [ 0 , π /2 ] ω > 0 \omega>0 ω > 0 ω \omega ω θ \theta θ
(1) 当细棒下摆至竖直位置时, θ = π 2 \theta = \frac{\pi}{2} θ = 2 π
角速度大小为
ω = 3 g l \omega = \sqrt{\frac{3g}{l}} ω = l 3 g .
(2) 在竖直位置 β = 3 2 g l cos π 2 = 0 \beta = \frac{3}{2} \frac{g}{l} \cos \frac{\pi}{2} = 0 β = 2 3 l g cos 2 π = 0 a c 1 = ( l / 2 ) β = 0 a_{c_1} = (l/2)\beta = 0 a c 1 = ( l /2 ) β = 0 a c 2 = ( l / 2 ) ω 2 = 3 g / 2 a_{c_2} = (l/2)\omega^2 = 3g/2 a c 2 = ( l /2 ) ω 2 = 3 g /2
(3) 在竖直位置时,转轴对细棒的作用 力可利用质心运动定理求出,即
切向:
F N t = m a C t = 0 F_{Nt} = ma_{Ct} = 0 F Nt = m a Ct = 0 法向: F N n F_{Nn} F N n Cn
将此时的 a c n a_{cn} a c n F N n = 5 m g / 2 F_{Nn}=5mg/2 F N n = 5 m g /2 O ∞ O_{\infty} O ∞
2.2.5 刚体的平衡
在惯性参考系中,一个刚体处于力学平衡状态的条件有两个:(1) 刚体质心的加速度 a c a_c a c β \beta β
根据质心运动定理,第一个条件要求刚体所受合外力的矢量 和等于零,即
∑ i F i = 0 ( 2.2.9 ) \sum_{i} F_{i} = 0 {(2.2.9)} i ∑ F i = 0 ( 2.2.9 ) 在盲角坐标系中,式(2.2.9)沿三个坐标轴的分量式为
{ ∑ i F x i = 0 ∑ i F y i = 0 ∑ i F z i = 0 \begin{cases} \sum_{i} F_{xi} = 0 \\ \sum_{i} F_{yi} = 0 \\ \sum_{i} F_{zi} = 0 \end{cases} ⎩ ⎨ ⎧ ∑ i F x i = 0 ∑ i F y i = 0 ∑ i F z i = 0 (2. 2. 10)
根据刚体的转动定律,第二个条件要求刚体所受合外力矩的矢量 和等于零,即
∑ i M i = 0 (2.2.11) \sum_{i} M_{i} = 0 \tag{2.2.11} i ∑ M i = 0 ( 2.2.11 ) 在直角坐标系中,式(2.2.11)沿三个坐标轴的分量式为
{ ∑ i M x i = 0 ∑ i M y i = 0 ∑ i M z i = 0 \begin{cases} \sum_{i} M_{xi} = 0 \\ \sum_{i} M_{yi} = 0 \\ \sum_{i} M_{zi} = 0 \end{cases} ⎩ ⎨ ⎧ ∑ i M x i = 0 ∑ i M y i = 0 ∑ i M z i = 0 (2. 2. 12)
由此可见,刚体平衡时必须满足6个独立的方程,即式(2.2.10)和式(2.2.12),这6个方程和刚体的6个自由度(3个平动自由度和3个转动自由度)相对应。这6个独立方程限制了刚体自由运动的6个自由度,也就限定了刚体的位置,刚体因而达到平衡。
当作用于刚体上的所有力都位于同一平面上时,刚体的三维平衡问题就转化为二维平衡问题。这时,刚体在平面上有2个平动自由度和1个转动自由度,只需要3个独立方程就能解决问题,即在该平面内沿任意两个互相垂直方向上的力(或力的分量)的代数和为零,并且相对任一垂直于该平面的转轴的力矩代数和为零。
例题 2-8
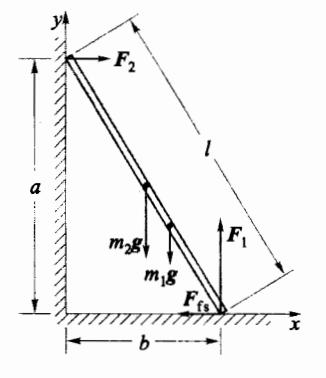
如图 2-12 所示,一长 l=6 m、质量 m 1 = 50 m_1=50 m 1 = 50 m 2 = 80 m_2=80 m 2 = 80 μ s = 0.4 \mu_s=0.4 μ s = 0.4
(1) 墙面与地面对梯子的作用力,此时梯子是否滑动?
(2) 在梯子开始滑动之前,人能沿梯子爬到多高的位置?
解:根据几何关系,梯子触地点与墙角距离 b = l 2 − a 2 = 3.6 m ⊙ b=\sqrt{l^2-a^2}=3.6~\mathrm{m}_{\odot} b = l 2 − a 2 = 3.6 m ⊙
(1) 取 x 轴沿着地面向右为正, y 轴沿
图 2-12 刚体的平衡
着墙面向上为正。梯子除受作用于自身质心大小为 m 1 g m_1g m 1 g m 2 g m_2g m 2 g F 2 F_2 F 2 F 1 F_1 F 1 F 4 F_4 F 4
F 2 − F f s = 0 F_2 - F_{fs} = 0 F 2 − F f s = 0 F 1 − m 1 g − m 2 g = 0 F_1 - m_1 g - m_2 g = 0 F 1 − m 1 g − m 2 g = 0
除此之外,还要满足围绕某一与 xy 平面垂直的转轴的合力矩为零,至于转轴的位置可以任选。例如,选取通过梯子触地点并垂直 xy 平面的转轴,并规定顺时针旋转为正向,相对此轴的合力矩应该为零,即
F 2 a − m 2 g b 2 − m 1 g b 3 = 0 F_2 a - m_2 g \frac{b}{2} - m_1 g \frac{b}{3} = 0 F 2 a − m 2 g 2 b − m 1 g 3 b = 0 由以上三个方程解出: F 1 = ( m 1 + m 2 ) g = F_1 = (m_1 + m_2)g = F 1 = ( m 1 + m 2 ) g =
1 274 N,
F t 0 = F 2 = b g a ( m 2 2 + m 1 3 ) = 416.5 N , ± 100 F_{t_0} = F_2 = \frac{bg}{a} \left( \frac{m_2}{2} + \frac{m_1}{3} \right) = 416.5 \text{ N}, \pm 100 F t 0 = F 2 = a b g ( 2 m 2 + 3 m 1 ) = 416.5 N , ± 100 面对梯子的最大静摩擦力数值为 F femax = μ ∙ F 1 = 509.6 N F_{\text{femax}} = \mu_{\bullet}F_{1} = 509.6 \text{ N} F femax = μ ∙ F 1 = 509.6 N F f ∙ < F femax F_{f_{\bullet}} < F_{\text{femax}} F f ∙ < F femax
(2) 设梯子开始滑动之前,人沿梯子最多能爬 h 距离,令比值 h/l = k;此时摩擦力等于最大静摩擦力 F t a = F t s m a x = μ a F 1 F_{ta} = F_{tsmax} = \mu_a F_1 F t a = F t s ma x = μ a F 1
F 2 − μ s F 1 = 0 F_{2}-\mu_{s}F_{1} = 0 F 2 − μ s F 1 = 0 F 1 − m 1 g − m 2 g = 0 F_{1}-m_{1}g-m_{2}g = 0 F 1 − m 1 g − m 2 g = 0 F 2 a − m 2 g b k − m 1 g b 3 = 0 F_{2}a-m_{2}gbk-m_{1}g\frac{b}{3} = 0 F 2 a − m 2 g bk − m 1 g 3 b = 0 解得
k = 1 m 2 g b ( F 2 a − m 1 g b 3 ) k = \frac{1}{m_2 g b} \left( F_2 a - \frac{m_1 g b}{3} \right) k = m 2 g b 1 ( F 2 a − 3 m 1 g b ) = 1 m 2 b [ μ s ( m 1 + m 2 ) a − m 1 b 3 ] = 79 120 = \frac{1}{m_2 b} \left[ \mu_s (m_1 + m_2) a - \frac{m_1 b}{3} \right] = \frac{79}{120} = m 2 b 1 [ μ s ( m 1 + m 2 ) a − 3 m 1 b ] = 120 79 得 h = kl = 3.95 m。