1.6 质心运动定理

1.6.1 质心

前面已经多次出现,由若干质点组成的系统称为质点系。其实,任何一个物体都可以看作是由大量质点组成的质点系。在研究质点系的整体运动规律时,经常用到质量中心的概念,质量中心也简称质心。

设一个质点系由n个质点组成,其中第i个质点的质量为 $m_i$ ,相对坐标原点O的位矢为 $r_i$ ,则质心的位矢 $r_c$ 定义为

$$r_c = \frac{\sum_{i=1}^{n} m_i \mathbf{r}_i}{\sum_{i=1}^{n} m_i} = \frac{\sum_{i=1}^{n} m_i \mathbf{r}_i}{m} \tag{1.6.1}$$

式中 $,m=\sum_{i=1}^{n}m_{i}$ 为质点系的总质量。质心的位矢与坐标系的选择有关,但质心与质点系内各个质点的相对位置则与坐标系的选择无关。式(1.6.1)在直角坐标系中的分量式为

$$x_c = \frac{\sum_{i=1}^{n} m_i x_i}{m},\quad y_c = \frac{\sum_{i=1}^{n} m_i y_i}{m},\quad z_c = \frac{\sum_{i=1}^{n} m_i z_i}{m}\tag{1.6.2}$$

如果质点系由连续分布的质点组成,则改用积分定义为

$$\mathbf{r}_c = \frac{\int \mathbf{r} \, d\mathbf{m}}{\int d\mathbf{m}} = \frac{\int \mathbf{r} \, d\mathbf{m}}{\mathbf{m}} \tag{1.6.3}$$

式中 $m = \int dm$ 为质点系的总质量,式中的积分遍及质点系。式 (1.6.3) 在直角坐标系中的分量式为

$$x_c = \frac{\int x dm}{m},\quad y_c = \frac{\int y dm}{m},\quad z_c = \frac{\int z dm}{m}\tag{1.6.4}$$

对于质量均匀分布、形状规则的几何形体来说,其质心的位置与其几何中心重合。而一般来说,质心的位置可能处于物体的内部,也可能处于物体的外部。

例题 1-18

有一质量为 m、半径为 R、圆心角为 $2\theta$ 的扇形薄板,质量均匀分布,如图 1-37 所示。求薄板质心的位置。

解:选扇形板面与 Oxy 直角坐标平面重合,扇形圆心为坐标原点,x 轴平分圆心角。根据对称性,显然有质心的 y 坐标为零,即 $y_c=0$ ;由于形状为扇形,所以转换为平面极坐标更为方便。距离圆心为 r 处面积元的面积为 $dA=rd\alpha dr$ ,由几何知识可知此扇形面积为 $A=R^2\theta$ ,薄板单位面积的质量为 $\sigma=\frac{m}{R^2\theta}$ ,面积元的质量为 $dm=\sigma dA$ ,面积元的 x 坐标为 $x=r\cos\alpha$ 。将各量代入到式(1.6.4)中的 $x_c$ 式,有

图 1-37 扇形薄板的质心

$$x_{c} = \frac{1}{m} \int x dm = \frac{1}{m} \int r \cos \alpha \sigma dA\\ = \frac{\sigma}{m} \int_{0}^{R} r^{2} dr \int_{-\theta}^{\theta} \cos \alpha d\alpha = \frac{2R}{3\theta} \sin \theta$$

若薄板形状为半圆,则 $\theta = \frac{\pi}{2}, x_c = \frac{4R}{3\pi}$ 。

1.6.2 质心运动定理

将式(1.6.1)对时间求导数,可得质心的速度 $v_c$ ,即

$$\boldsymbol{v}_{c} = \frac{\mathrm{d}\boldsymbol{r}_{c}}{\mathrm{d}t} = \frac{1}{m} \sum_{i=1}^{n} m_{i} \frac{\mathrm{d}\boldsymbol{r}_{i}}{\mathrm{d}t} = \frac{1}{m} \sum_{i=1}^{n} m_{i} \boldsymbol{v}_{i}$$

式中, $\sum_{i=1}^{n} m_i v_i = p$ 为质点系的动量,在前文中已经出现过。将其代人,有

$$\boldsymbol{p} = m\boldsymbol{v}_C = \boldsymbol{p}_C \tag{1.6.5}$$

可见,质点系的动量等于质心的动量。根据质点系的动量定理,即式(1.4.8),有

$$\int_{t_1}^{t_2} \sum_{i=1}^{n} \mathbf{F}_i dt = \mathbf{p}_{c2} - \mathbf{p}_{c1} = m \mathbf{v}_{c2} - m \mathbf{v}_{c1}$$

其相应的微分关系式为

$$\sum_{i=1}^{n} \mathbf{F}_{i} = \frac{\mathrm{d}\mathbf{p}_{c}}{\mathrm{d}t} = m \frac{\mathrm{d}\mathbf{v}_{c}}{\mathrm{d}t} = m \mathbf{a}_{c} \tag{1.6.6}$$

由此看来:质点系的运动等同于一个质点的运动,服从牛顿运动定律。这个质点的质量等于质点系的总质量,这个质点的位置为质点系质心的位置。式(1.6.6)表明,质点系所受的合外力等于质点系质心动量的时间变化率,这称为质心运动定理。

根据质心运动定理,当质点系不受外力或所受合外力为零时,质心保持静止或匀速直线运动状态不变。换句话说就是,系统的内力不能改变系统质心的运动状态。而对于只有重力作用的抛体运动,则不论物体在空中如何翻滚,其质心的运动轨迹仍是抛物线。像高台跳水运动员,离开跳台后的运动情况就是如此。

例题 1-19

长为l质量为m的软绳,开始时竖直悬挂着,下端刚好触地;现使软绳从静止状态自由下落。求软绳下落到空中所剩长度为z时地面对绳子的作用力,如图 1-38 所示。

解:自地面垂直向上作为 z 坐标轴,将整根绳子作为所研究的质点系。绳子单位长度的质量为 $\lambda = m/l$ ,已落地的线元坐标为 0,空中部分坐标 z 处线元的质量为 $dm = \lambda dz$ ,由式(1.6.4)得软绳的质心坐标

$$z_{c} = \frac{1}{m} \int_{0}^{z} z dm = \frac{1}{m} \int_{0}^{z} \lambda z dz\\ = \frac{1}{m} \int_{0}^{z} \frac{m}{l} z dz = \frac{z^{2}}{2l}$$

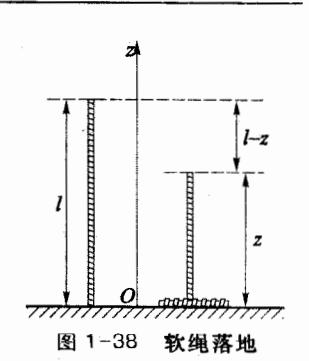
质心速度 $v_c = \frac{\mathrm{d}z_c}{\mathrm{d}t} = \frac{z}{l} \frac{\mathrm{d}z}{\mathrm{d}t}$ , 其中 $\frac{\mathrm{d}z}{\mathrm{d}t} = v$ 是绳子空中部分的下落速度, 对于柔软的绳子来说, 该下落速度与质点自由落体的速度相同, 所以 $v = -\sqrt{2g(l-z)}$ , 负号表示 v 与 z 轴正向相反。质心的加速度为

$$a_c = \frac{\mathrm{d}v_c}{\mathrm{d}t} = \frac{\mathrm{d}}{\mathrm{d}t} \left(\frac{z}{l}v\right) = \frac{v^2}{l} + \frac{z}{l} \frac{\mathrm{d}v}{\mathrm{d}t}$$

式中, $\frac{dv}{dt} = -g$ 为绳子下落的加速度,代人上式,有

$$a_c = \frac{g}{l}(2l - 3z)$$

系统所受外力有:地面支持力 $F_N$ 竖直向上,重力mg 竖直向下。根据质心运动定理,有 $F_N-mg=ma_c$

将 $a_c$ 代入,解出地面对绳子的作用力为

$$F_{\rm N} = 3mg\left(1 - \frac{z}{l}\right)$$

思考题与习题

• 1 1 对一个质点来说, $\frac{dv}{dt}$ 、 $\frac{dr}{dt}$ 、 $\frac{ds}{dt}$ 、 $\frac{dv}{dt}$ 、 $\left|\frac{dv}{dt}\right|$ 各表示什么物理意义?
• 1.2 设质点做曲线运动的方程为 x=x(t) 和 y=y(t), 在计算质点的速度和加速度的数值时, 有人先求出 $r=\sqrt{x^2+y^2}$ , 再由 $v=\frac{\mathrm{d}r}{\mathrm{d}t}$ 和 $a=\frac{\mathrm{d}^2r}{\mathrm{d}t^2}$ 求得 v 和 a。这种方法对吗? 怎样做才是正确的?
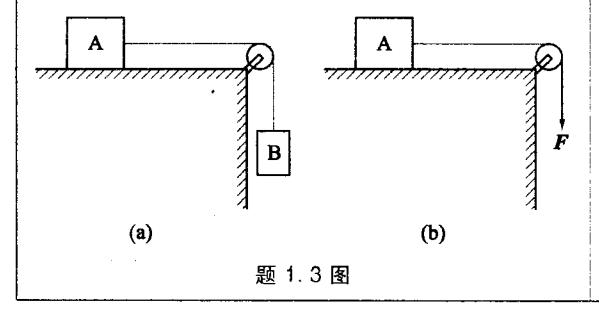
• 1.3 在光滑的水平桌面上,用跨过定滑轮的绳子拉动物体 A,设定滑轮和绳子的质量可以忽略。问在下面两种情况下,物体 A 的加速度是否相同?绳中的张力是否相同?
• (1) 在绳子的另一端挂上质量为 $m_B = 5 \text{ kg}$ 的物体 B[题 1.3 图(a)];

• (2) 在绳子的另一端用力 F=m_Bg 向下拉[题 1.3 图(b)]。

• 1.4 以力 F 拉弹簧,弹簧伸长 $\Delta L$ 。如果以两个这样的弹簧组成系统,在下述两种组合中,要使系统同样伸长 $\Delta L$ ,要用多大的力?

  • (1) 两个弹簧串联;
  • (2) 两个弹簧并联。

• 1.5 关于摩擦力的概念有种种说法,试指出下面的几种说法是否正确?并举例说明。

  • (1) 摩擦力总是与物体运动的方向相反;
  • (2) 摩擦力总是做负功;
  • (3) 摩擦力总是阻碍着物体间的相对运动。

• 1.6 绳子通过高处的定滑轮,两端分别攀着两只质量相同的猴子,开始时它们离地面的高度相同,设它们同时攀绳往上爬,其中一只相对绳的速度总是另一只相对绳的速度的两倍。问哪一只先爬到顶点?

• 1.7 把一块很长的木板安装上轮子,放在光滑的平面上,有两人在板上从板的两端相向行走,在下述的三种情况中,木板向哪个方向运动?

  • (1) 两人的质量相同,速度的大小相同;

• (2) 两人的质量不同,而速度大小相同;

• (3) 两人的质量相同,而速度大小不同。

• 1.8 两质点有相同的动量 p, 相对于同一参考点来说, 它们的角动量是否一定相同?

• 1.9 单摆在单向的摆动过程中,如果忽略了摩擦,角动量的方向是否变化? 角动量的大小是否变化?

• 1.10 根据动量定理,给物体以冲量作用,必引起物体动量的改变;根据动能定理,力对物体做功,必引起物体动能的改变。

• (1) 给物体以冲量作用,是否一定会引起动能的改变?

  • (2) 对物体做了功,是否一定会引起动量的改变?

• 1.11 一木块的质量为 m',用细绳悬挂着,可在竖直平面内摆动。今有一质量为 m 的子弹沿水平方向射人木块,并陷在其中,和木块一起升高了 h。为了计算子弹人射前的速度 v,采用公式 $\frac{1}{2}mv^2 = (m'+m)gh$ 对否?为什么?

• 1. 12 有一质点沿 x 轴做直线运动,t 时刻的坐标为 $x=4.5t^2-2t^3$ ,式中 x 的单位为 m,t 的单位为 s。试求:
  • (1) 从 t=1 s 到 t=2 s 之间的路程;
  • (2) 从 t=1 s到 t=2 s 之间的位移及平均速度;
  • (3) t=1 s 时的速度和加速度。
• 1. 13 一个质点在 xy 平面上运动,运动方程 $x = 3t + 5, y = \frac{t^2}{2} + 3t 4(SI 单位)。求:$
  • (1) 位置矢量;
  • (2) 从 t=1 s 到 t=2 s 的位移;
  • (3) 轨道方程;
  • (4) t=4 s 时的速度:
  • (5) t=4 s 时的加速度;
  • (6) t=4 s 时的切向加速度、法向加速度。

• 1.14 一粒子沿拋物线轨道 $y=x^2$ 运动,粒子速度沿 x 轴的投影恒为 $v_x=3$ m·s^-1,求当坐标 x=2/3 m时,粒子的速度和加速度。

• 1.15 在光滑水平桌面上有一根细棒绕棒的一端 0 旋转,如以 0 为极点,沿一固定方向作射线为极轴,则相对极轴细棒旋转角度与时间的关系为 $\theta$ = 0.4t(rad·s^-1)。现在棒上有一只昆虫在 t = 0 时,从 0 点出发沿棒向外爬行,昆虫相对棒的速度恒为 u = 0.01 m·s^-1。求当 t = 2 s 时,昆虫相对桌面的径向速度、横向速度及总速度的大小。

• 1.16 在一个半径为 R 的定滑轮上缠绕着一根质量可以忽略的绳子,悬在绳子一端的物体在竖直方向按 $y = \frac{1}{2}bt^2$ 的规律运动,其中 b 为常量,t 为时间。设滑轮与绳子之间没有相对滑动,试求:滑轮边缘一点 M 在 t 时刻的速度、切向加速度、法向加速度和总加速度的大小。

题 1.16图

• 1.17 有一做直线运动的物体,其速度与时间的 关系曲线如图所示。求:
  • (1) t=2 s, t=6 s, t=10 s 时的加速度:
  • (2) 前 4 s、前 8 s、前 12 s 内物体运动的距离。

题 1.17图

• 1.18 一质点沿直线运动,加速度 $a=4-t^2$ (m·s^-2),如果当 t=3 s 时,质点位置为 x=9 m,速度为 v=2 m·s^-1,求质点的坐标与时间的关系。
• 1. 19 一辆汽车冒雨沿平直的公路行驶,当车的速率为 $v=6~km \cdot h^{-1}$ 时,车窗上的雨迹为竖直向下。当车的速率为 $v=18~km \cdot h^{-1}$ 时,车窗上的雨迹向车后倾斜且与竖直方向成 $30^{\circ}$ 角。求雨点的速率与下落方向。
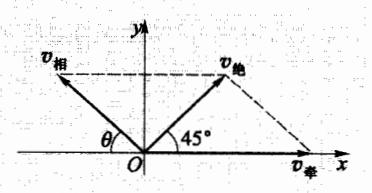
• 1.20 在海面上有两艘船航行,甲船以30 km·h^-1的速度向东航行,乙船以20 km·h^-1的速度向东北航行,求乙船相对甲船的速度。

题 1.20 图

• 1.21 质点质量 m=2 kg,运动方程为 $r=4t^4i+(1-2t^3)j(m)$ ,其中时间 t 的单位为 s。求:
  • (1) 质点所受合外力的表达式;
  • (2) 当 t=1 s 时合外力的大小及与 z 轴的夹角。
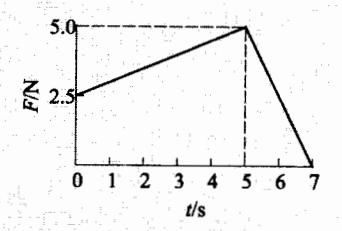
• 1.22 水平桌面上有一质量 m=1 kg 的物体,在水平拉力 F 的作用下由静止开始沿直线运动,拉力 F 随时间 t 的变化关系如图所示。已知物体与桌面之间的动摩擦因数 $\mu_k=0$ . 25,求物体在 t=5 s 和 t=7 s 时的速度大小。

题 1.22图

1.23 如图所示,在一根长为 R 的轻绳的一端系一质量为 m 的小球,另一端固定于 O 点,使小球在竖直平面内做圆周运动。已知 t=0 时,小球处在最低点且速率为 $v_0$ ,求小球在任意位置时的速率和绳中张力的大小,讨论小球做圆运动时速率 $v_0$ 所须满足的条件。

题 1.23图

• 1. 24 质量 m=1 kg 的质点,受力 F=2ti(N) 的作用,式中 t 为时间,单位为 s。若 t=0 时该质点恰以 $v_0=2j$ $m\cdot s^{-1}$ 的速度通过坐标原点,求该质点任意时刻的位置矢量。
• 1.25 如图所示,长 L 的均质链条质量为 m,将 其一端拉起,使链条自由下垂,并下端触地。若让链 条下落,试求出地面对链条作用力的大小是如何随下 落高度 h 改变的?并求出该作用力的平均值。

1.26 升降机内有一装置如图所示,定滑轮两边悬挂的两个物体质量关系为 $m_1 > m_2$ 。设绳与滑轮质量可不计,滑轮轴处摩擦可忽略,绳不可伸长,滑轮与绳之间无相对滑动。当升降机向下以加速度 a 运动时,以升降机为参考系求绳子的张力及两物体的加速度。

题 1.26 图

1.27 如图所示,在加速行驶的火车上,有一倾角为30°的斜面,一物体置于此斜面上,物与斜面间静摩擦因数为0.2,欲使物体相对斜面静止,火车加速度应有怎样的限制?

题 1.27图

1. 28 在光滑的圆锥体内壁上有一小球,圆锥体绕其对称轴 z 做角速度为 $\omega$ 的匀角速转动,如图所示。已知圆锥体的锥角为 $\theta$ ,求 $\omega$ 取何值时,可使小球在距离圆锥体顶点为 l 处相对于圆锥体静止?

题 1.28 图

1. 29 一质点在几个力作用下的位移 $\Delta r = (3i + 8j + 5k)$ m,其中有一恒力 F = (12i - 3j + 4k) N,求该力做的功。

1.30 如图所示,物体 A、B 的质量 $m_A = m_B =$ 0.01 kg,物体 B 与桌面间的动摩擦因数 $\mu_k = 0.10$ ,滑轮及连接 A、B 的绳子质量可以忽略,且绳子不可伸长,滑轮轴处的摩擦不计。求物体 A 自静止下降 s = 1.0 m 时的速度大小。

题 1.30 图

1.31 如图所示,质量 m=2 kg 的物体,从静止开始沿着固定于地面的 1/4 圆弧从 A 滑到 B,到达 B 处时的速度为 v=6 m·s^-1,已知圆弧的半径 R=4 m。求物体从 A 滑到 B 过程中摩擦力所做的功。

题 1.31 图

1.32 如图所示,变力 F 沿着半径为 $\alpha$ 的光滑圆柱面的切向方向,在准平衡态的情况下向上拉一木块。木块质量为 m,下系一劲度系数为 k 的轻弹簧,弹簧的原长为 l。求力 F 从弹簧位置 1 拉到位置 2 的过程中所做的功(1 和 2 之间的圆弧所对应的圆心角为 $\theta_{\alpha}$ )。

题 1.32 图

• 1.33 在光滑桌面上,一质量 m=2 kg 的质点在力 $F=26.4x+19.2x^2$ (N)作用下由静止出发沿 x 轴从 $x_1=0.50$ m 处运动到 $x_2=1.00$ m 处,若力 F 的方向始终与质点运动方向相同,求该力所做功及质点在 $x_2$ 处的速率。
  • 1.34 在光滑的水平面上,平放着如图所示的固

定半圆形屏障。质量为 m 的滑块以初速度 vo 沿切线方向进入 屏障内,滑块与屏障间的动摩擦因数为 μ,,试证明当滑块从 屏障另一端滑出时,摩擦力所 做的功为

The diagram shows a block starting with initial velocity $v_{0}$ at the top of a semi-circular track.

题1. 24图

$$W = \frac{1}{2} m v_0^2 (e^{-2\pi\mu_1} - 1)$$

提示:利用动能定理。

题 1.34 图

• 1.35 力 F 作用在质量 m=2 kg 的质点上,使之沿 z 轴运动。已知在此力作用下质点的运动方程为 $z=3+5\iota+6\iota^2-\iota^3$ ,其中时间 $\iota$ 的单位为 s,z 的单位为 m。求该力在 $\iota=0$ 至 $\iota=4$ s 内的冲量。
• 1.36 一质量 m=3 kg 的质点在力 F=75-30t (N)作用下,从 t=0 时刻由静止出发做直线运动,当 t=4 s 时,该力的冲量是多少? 质点的速率是多少?
• 1.37 如图所示为一锻压机,质量 m=2000 kg 的重锤从高度 h=1.5 m 处自然落到工件上,如果作用时间 $\Delta t=0.01$ s,试求重锤对工件的平均冲力。

题 1.37图

• 1.38 质量 m = 50 kg 的人站在一条小船的尾部,船静止于湖面上。小船长度 l = 4 m ,质量 m' = 150 kg 求当人从船尾走到船头的过程中,人相对湖岸的位移。(水对船的摩擦力可忽略。)
• 1. 39 一个质量为 m = 3.0 kg 的质点位于 r = (3i+8j) m 处时的速度为 v = (5i-6j) m·s^-1,此刻一力 F = -7i N 作用在该质点上,求:
  • (1) 质点的角动量;
  • (2) 质点所受的力矩;
  • (3) 质点角动量的时间变化率。
• 1.40 一颗人造卫星绕地球做椭圆轨道运动,在近地点的速度为 8.1 km·s^-1,距离地面的高度为 439 km;在远地点时,距离地面的高度为 2 384 km。地球半径 R=6 371 km,求卫星在远地点时的速度为多少?
• 1.41 如图所示,在光滑桌面上,静止滑块 $m_1$ 位于距 0 点 r 处, $m_1$ 与 0 点间用不可伸长的轻绳相连, 绳长 l > r。现有一质量 $m_2 = m_1$ 的子弹以速度 $v_0$ 射人滑块并嵌入其中, $v_0$ 的方向与 0 点的垂直距离为 a。求:
• (1) 滑块与子弹以绳长为半径绕 0 做圆周运动时的速率;
  • (2) 此时的动能与初态子弹的动能之比。

1.42 如图所示,在光滑水平面上有一轻弹簧,它的一端固定于 O 点,另一端系一质量为 m=1 kg 的滑块,弹簧原长 $l_0=0.2$ m,劲度系数 k=100 N·m^-1。开始时滑块在弹簧原长 $l_0$ 处,速度 $v_0=5$ m·s^-1,速度

方向与弹簧垂直。求此后某一时刻当弹簧长度 l=0.5 m时,滑块速度 v 的大小及与弹簧长度方向的夹角 $\theta$ 。

题 1.42 图

1.43 求腰长为 a 的等腰直角三角形均匀薄板的质心位置。

题 1.43 图

• 1.44 在摩天楼顶相隔 1 s 先后释放了两枚石子 使它们自由下落,第一粒石子质量为 20 g,第二粒石子 质量为50 g。求:在第二粒石子释放 3 s 后,两石子系 统质心的速度和加速度的大小。
• 1.45 一条质量均匀分布的细绳,单位长度的质量为 ( \lambda ),开始时盘绕在光滑的水平桌面上。现有一力垂直向上提起绳的一端,分别按下列两种情况求当提起高度为 ( ( x ) 从于绳长)时作用于绳端力的大小。
  • (1) 以恒定速度 v 向上提绳;
• (2) 以恒定加速度 a 向上提绳。(提示:利用质心运动定理。)